- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа на тему Логарифмические уравнения (11класс)
Содержание
- 1. Презентация по алгебре и началам анализа на тему Логарифмические уравнения (11класс)
- 2. Определение Уравнение, содержащее переменную под знаком логарифма, называется логарифмическимГде ,Оно имеет единственное решение при любом b.
- 3. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
- 4. Логарифмические неравенства
- 5. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
- 6. Логарифмические уравнения – Решу ЕГЭ.
- 7. ПроблемаДефицит методов решения экзаменационных логарифмических неравенств, предлагаемых
- 8. Учебно-исследовательскиемини-проекты
- 9. «Логарифмы и логарифмическая функция в природе и
- 10. Логарифмы и логарифмическая функцияДесятичный логарифм:lg a =
- 11. ЛОГАРИФМЫ В ПРИРОДЕЯркость источников света - шкала
- 12. ХИМИЧЕСКАЯ ЧУВСТВИТЕЛЬНОСТЬ — ШКАЛА КИСЛОТНОСТИ Первымихимическимииндикаторами былинаши вкусовыерецепторы, которымисегодня пользуютсятолько повара,а раньшеПользовалисьи химики.
- 13. ВОСПРИЯТИЕ ПСИХИЧЕСКИХ ЯВЛЕНИЙ — ШКАЛА ЭМОЦИЙ Воспоминание академика
- 14. ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА ВЫЧИСЛЕНИЕ ЛОГАРИФМОВ,
- 15. Использование логарифмической линейки в ХХl веке
- 16. ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ, плоская кривая, описываемая точкой, движущейся
- 17. Слайд 17
- 18. Логарифмическая спираль в техникеЛогарифмическая спираль пересекает свои
- 19. ЗаключениеПоистине безграничны приложения логарифмической функции и логарифмов
- 20. Равносильные уравнения. Определение 1. Два уравнения с одной переменной
- 21. Определение 2. Если каждый корень уравнения
- 22. Определение 3. Два уравнения равносильны тогда и только
- 23. Основные методы решения логарифмических уравненийпо определению логарифма;например,
- 24. 3) метод потенцирования;Под потенцированием понимается переход от
- 25. 4. Метод введение новой переменной. 5. Метод
- 26. Этапы решения уравненияНайти область допустимых значений (ОДЗ)
- 27. Виды простейших логарифмических уравнений и методы их решения
- 28. Уравнения вида loga f(x) = b, a
- 29. Уравнения вида logf(x) b = с, b > 0. Данное уравнение равносильно следующей системе
- 30. Решить уравнения:1. log3(5х – 1) = 2.2.
- 31. Метод потенцирования применяется в том случае, если
- 32. log2х – 2 logх2 = –1Решение: ОДЗ:
- 33. Обозначим
- 34. Решить уравнения:
- 35. Введение новой переменной где a >
- 36. Пример 1. Решить уравнение lg 2 x
- 37. Вернёмся к первоначальной переменной lg x =
- 38. Пример 2. Решить уравнениеРешение. Найдём область определения уравненияПрименив формулу логарифма степени, получим уравнение
- 39. Так как х < 0, то | x | = –x и следовательно
- 40. Решить уравнения
- 41. Найдём область определения уравнения:2-x >0x-1 >0Область определения уравнения 1
- 42. Решить уравнениеОбласть определения уравнения x > 1х = 6
- 43. Решить уравнениеУмножим обе части уравнения на log 3(x + 1) (log 3(x +
- 44. Решить уравнениеТак как при х > 0 обе части уравнения положительны,
- 45. Решить уравнениеlogb a + logb c = logb (ac)
- 46. Найдём область определения уравненияРешить уравнениеТак как х <
- 47. Решить уравнение lg2100x + lg210x + lgx = 14 lg2100x + lg210x + lgx =
- 48. Решить уравнение Область определения уравнения определяется условиямиДанный корень удовлетворяет области определения уравнения
- 49. Уравнения – это золотой ключ, открывающий все
- 50. Учебно-исследовательский проект «Логарифмы в
- 51. Схема презентацииПроблемаЦельПланработыИсториявопросаПроектныйпродуктВыводы
- 52. ПроблемаДефицит методов решения экзаменационных логарифмических неравенств, предлагаемых
- 53. Слайд 53
- 54. План работы Подборка математической литературы по теме
- 55. История
- 56. Слайд 56
- 57. Методы решения уравненийРавносильные переходы и обобщённый метод интерваловМетод рационализацииНестандартная подстановкаЗадания с ловушками (свойства функций)
- 58. Пример из сборника
- 59. Пример из сборника
- 60. Содержание презентации «Логарифмы вокруг нас»Логарифмическая спиральЗвёзды и логарифмыШумы и логарифмыЖивопись и логарифмы
- 61. Логарифмическая спираль «Удивительное рядом»
- 62. Логарифмы и живопись Логарифмические линии
- 63. Выводы
- 64. Использованная литература1. Корянов А. Г. ,Прокофьев
- 65. Спасибо!
Слайд 1«ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
МКОУ «СОШ №32»
УЧИТЕЛЬ МАТЕМАТИКИ
ОРШОКДУГОВА РИММА МАЖИДОВНА.
11 «РН» КЛАСС
Слайд 2Определение
Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим
Где
,
Оно имеет
при любом b.
Слайд 7Проблема
Дефицит методов решения экзаменационных логарифмических неравенств, предлагаемых в С3.
Ответ на
Слайд 9«Логарифмы и логарифмическая функция в природе и технике»
Актуальность
Логарифмы появились в
Цель, задачи
Обучающая цель:
-научить видеть знакомое в незнакомом;
-расширить представление о логарифмической функции;
-рассмотреть применение ее свойств в нестандартных ситуациях;
Воспитательная цель:
-формировать целостную систему знаний и научного мировоззрения;
Развивающая цель:
- развитие творческого, критического интегративного мышления, развитие самостоятельности;
-развивать логическое мышление, познавательный интерес.
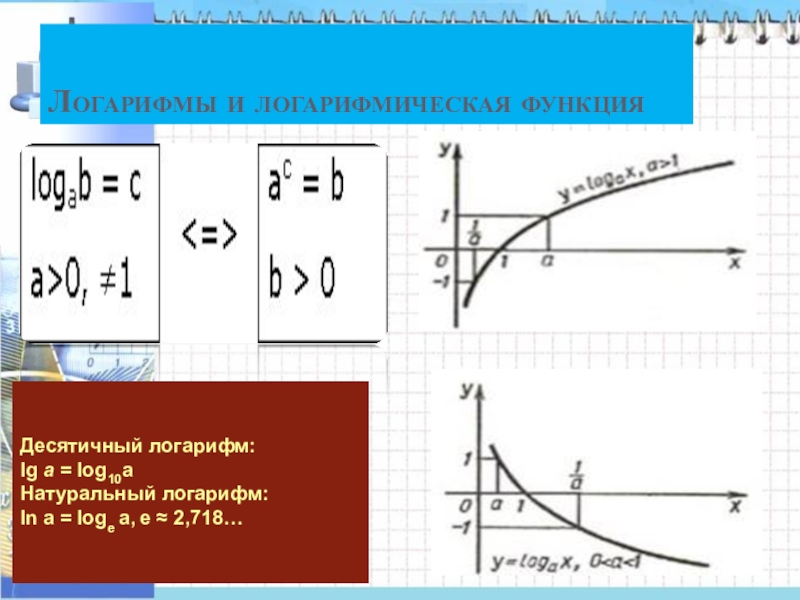
Слайд 10Логарифмы и логарифмическая функция
Десятичный логарифм:
lg a = log10a
Натуральный логарифм:
ln a
Слайд 11 ЛОГАРИФМЫ В ПРИРОДЕ
Яркость источников света - шкала звездных величин
Блеск в астрономии —
Астрономы измеряют «блеск» небесных светил в звездных величинах
Слайд 12
ХИМИЧЕСКАЯ ЧУВСТВИТЕЛЬНОСТЬ — ШКАЛА КИСЛОТНОСТИ
Первыми
химическими
индикаторами были
наши вкусовые
рецепторы, которыми
сегодня пользуются
только повара,
а раньше
Пользовались
и химики.
Слайд 13
ВОСПРИЯТИЕ ПСИХИЧЕСКИХ ЯВЛЕНИЙ — ШКАЛА ЭМОЦИЙ
Воспоминание академика В. Л. Гинзбурга: «… Ландау имел «шкалу заслуг»
Остается неясным, логарифм по какому основанию — 10 или 2,512… — использовал Лев Ландау для определения уровня гениальности физиков-теоретиков. Несомненно лишь одно: для этих сугубо эмоциональных, субъективных оценок он использовал логарифмическую шкалу.
Слайд 14 ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА ВЫЧИСЛЕНИЕ ЛОГАРИФМОВ, ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ И ДРУГИХ— АНАЛОГОВОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО,
Слайд 15Использование логарифмической линейки в ХХl веке
Однако в начале
Слайд 16
ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ, плоская кривая, описываемая точкой, движущейся по прямой, которая вращается
ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ
Раковины многих моллюсков, улиток, а также рога горных козлов закручены по логарифмической спирали
Слайд 17
Никогда еще в природе не существовало столь совершенного примера логарифмических спиралей…)
Логарифмические
картина Вермера «Кружевница»
Слайд 18Логарифмическая спираль в технике
Логарифмическая спираль пересекает свои радиус-векторы под постоянным углом.
Это свойство находит свое применение в технике. Дело в том, что в технике часто применяются вращающиеся ножи. Сила с которой они давят на разрезаемый материал, зависит от угла резания, т.е. угла между лезвием ножа и направлением скорости вращения. Для постоянного давления нужно, чтобы угол резания сохранял постоянное значение, а это будет в том случае, если лезвия ножей очерчены по дуге логарифмической спирали. Величина угла резания зависит от обрабатываемого материала.
В гидротехнике по логарифмической спирали изгибают трубу, проводящую поток воды к лопастям турбины. Благодаря такой форме трубы потери энергии на изменение направления течения в трубе оказываются минимальными и напор воды используется с максимальной производительностью.
Нажимая на клавиши современного рояля, мы, можно сказать, играем на логарифмах.
Слайд 19Заключение
Поистине безграничны приложения логарифмической функции и логарифмов в самых различных областях
Многообразное применение функции вдохновило английского поэта Э. Брилла на написание оды о логарифмах.
Были поэты, которые не посвящали логарифмам целых од, но упоминали их в своих стихах. Известный поэт Борис Слуцкий в своём нашумевшем стихотворении «Физики и лирики» писал:
«Потому-то, словно пена,
Опадают наши рифмы
И величие степенно
Отступает в логарифмы».
Выполняя данную работу, я сделала для себя открытие, что логарифмы и логарифмическая функция помогли человеку следовать путём технического прогресса и объяснить многие тайны природы, человеческих ощущений. Быть может человечество стоит на пороге новых революционных открытий, и поможет нам в этом «царица наук»- математика!
Слайд 20Равносильные уравнения.
Определение 1. Два уравнения с одной переменной и называют равносильными, если
Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни
(например и ) или если оба уравнения не имеют корней (например , и )
Слайд 21Определение 2. Если каждый корень уравнения
Например, уравнение является следствием уравнения
, в то же время уравнение
не является следствием
уравнения .
Слайд 22Определение 3. Два уравнения равносильны тогда и только тогда, когда каждое из
Определение 4. Областью допустимых значений (ОДЗ) уравнения называют множество тех значений переменной, при которых одновременно имеют смысл выражения и .
Слайд 23Основные методы решения логарифмических уравнений
по определению логарифма;
например, уравнение loga х =
2) функционально-графический метод;
Слайд 243) метод потенцирования;
Под потенцированием понимается переход от равенства, содержащего логарифмы, к
Слайд 254. Метод введение новой переменной.
5. Метод логарифмирования обеих частей уравнения.
6. Метод приведения логарифмов к одному и тому же основанию.
Слайд 26Этапы решения уравнения
Найти область допустимых значений (ОДЗ) переменной
Решить уравнение, выбрав метод
Проверить найденные корни непосредственной подстановкой в исходное уравнение или выяснить, удовлетворяют ли они условиям ОДЗ
Слайд 28Уравнения вида
loga f(x) = b, a > 0, a ≠
Уравнения данного вида решаются по определению логарифма с учётом области определения функции f(x). Уравнение равносильно следующей системе
Слайд 30Решить уравнения:
1. log3(5х – 1) = 2.
2. log2(х – 5) +
3. log3 (x2 – 3x – 5) = log3 (7 – 2x).
4. logx–19 = 2.
5. log6 (x – 1) = 2 – log6 (5x + 3).
Слайд 31Метод потенцирования применяется в том случае, если все логарифмы, входящие в
Слайд 32log2х – 2 logх2 = –1
Решение: ОДЗ: x > 0, х
Используя формулу перехода к новому основанию, получим
Слайд 35Введение новой переменной
где a > 0, a ≠ 1,
Пусть t = loga f(x), t∈R. Уравнение примет вид t2 + Bt + C = 0.
Решив его, найдём х из подстановки t = loga f(x). Учитывая область определения, выберем только те значения x, которые удовлетворяют неравенству f(x) > 0.
Слайд 36Пример 1.
Решить уравнение lg 2 x – lg x –
Решение. Область определения уравнения – интервал (0; ∞).
Введём новую переменную t = lg x, t∈R.
Уравнение примет вид t 2 – t – 6 = 0.
Его корни t1 = –2, t2 = 3.
Слайд 37Вернёмся к первоначальной переменной lg x = –2 или lg x
х = 10 –2 или х = 10 3.
Оба значения x удовлетворяют
области определения данного уравнения (х > 0).
Ответ. х = 0,01; х = 1000.
Слайд 38Пример 2. Решить уравнение
Решение. Найдём область определения уравнения
Применив формулу логарифма степени,
Слайд 41
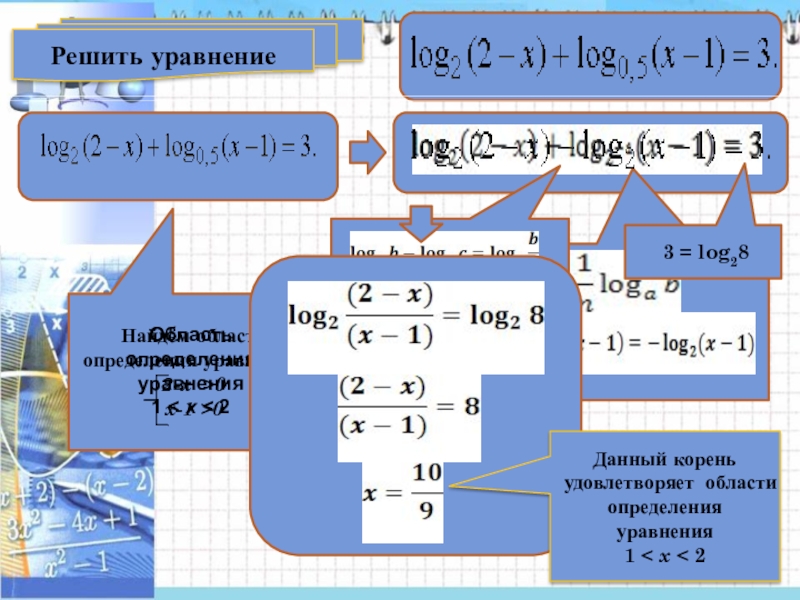
Найдём область определения уравнения:
2-x >0
x-1 >0
Область определения уравнения
1
Данный корень удовлетворяет области определения уравнения
1 < x < 2
Слайд 43
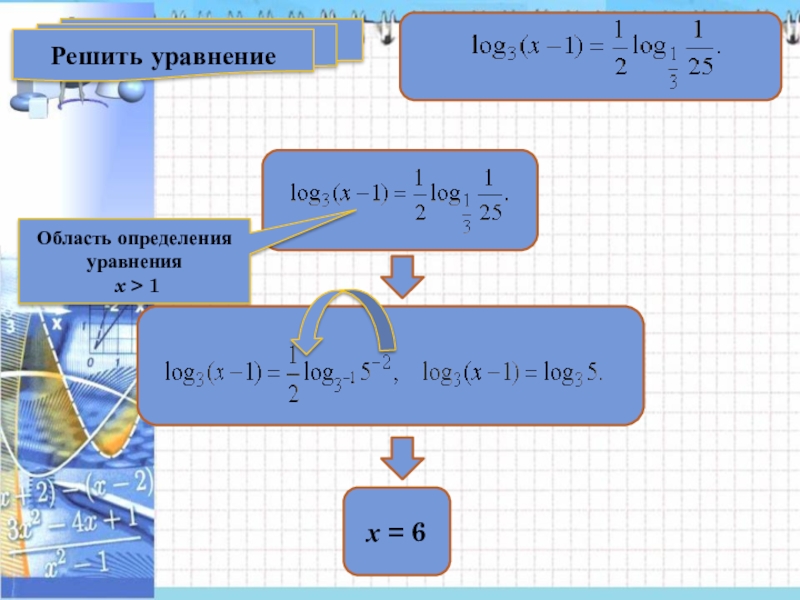
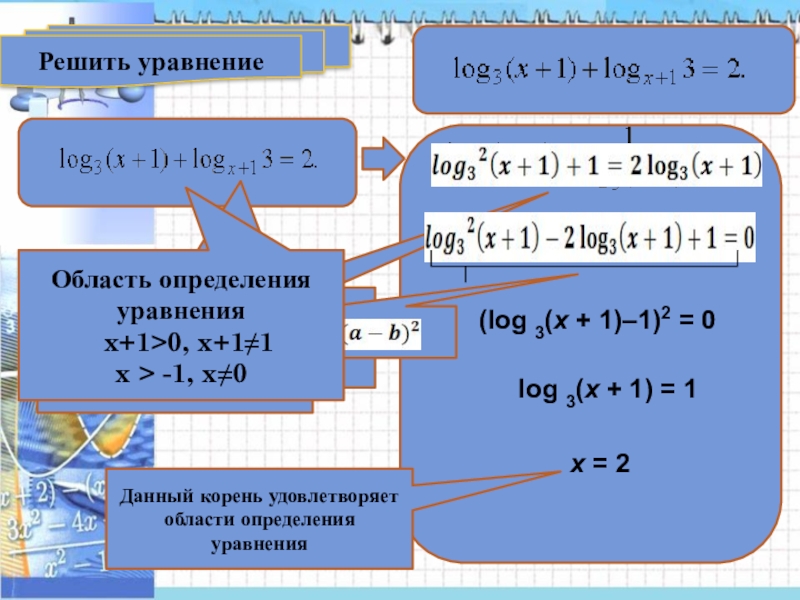
Решить уравнение
Умножим обе части уравнения на log 3(x + 1)
(log 3(x + 1)–1)2 = 0
log 3(x + 1) =
x = 2
Область определения уравнения
x+1>0, x+1≠1
x > -1, x≠0
Данный корень удовлетворяет
области определения уравнения
Слайд 44
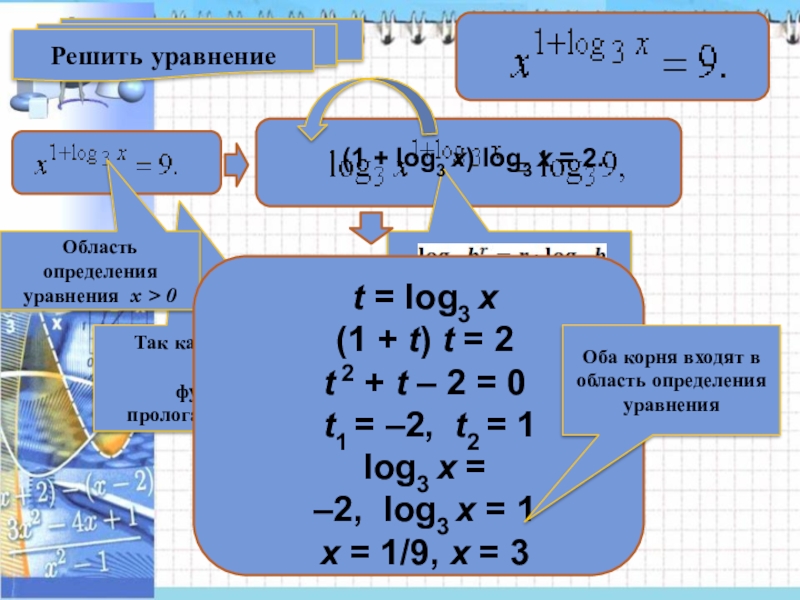
Решить уравнение
Так как при х > 0 обе части уравнения положительны, а функция y = log3 t монотонна прологарифмируем обе
Область определения уравнения x > 0
(1 + log3 x) log3 x = 2.
t = log3 x
(1 + t) t = 2
t 2 + t – 2 = 0
t1 = –2, t2 = 1
log3 x = –2, log3 x = 1
x = 1/9, х = 3
Оба корня входят в область определения уравнения
Слайд 46
Найдём область определения уравнения
Решить уравнение
Так как х < 0,
то | x | = –x
t = log3 (–x)
t 2 – 4t +
t1,2 = 2
log3 (–x) = 2
–х = 9
х = –9
Данный корень входит в область определения уравнения
Слайд 47
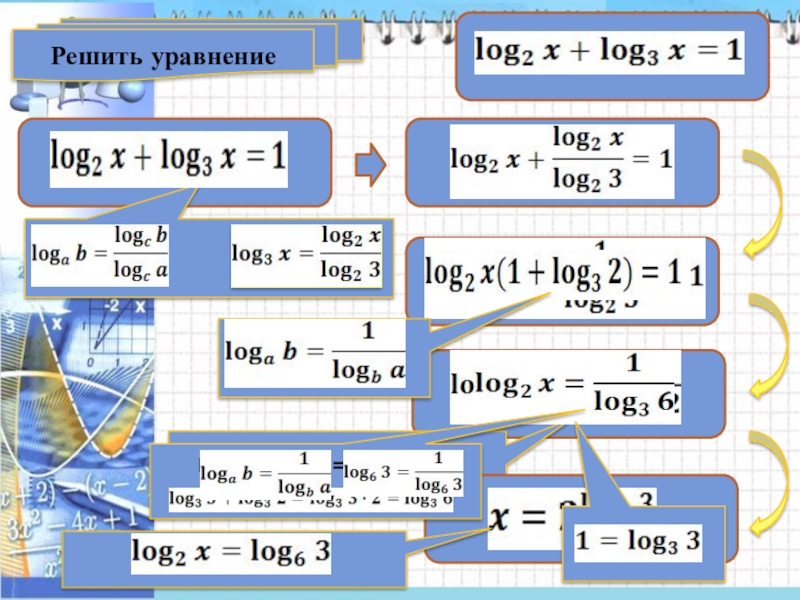
Решить уравнение
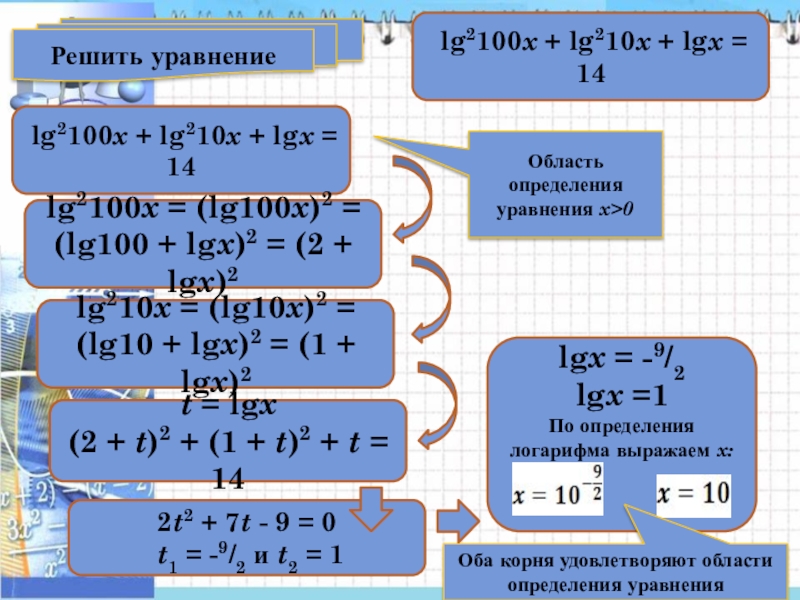
lg2100x + lg210x + lgx = 14
lg2100x + lg210x + lgx = 14
lg2100x = (lg100x)2 = (lg100 +
lg210x = (lg10x)2 = (lg10 + lgx)2 = (1 + lgx)2
t = lgx
(2 + t)2 + (1 + t)2 + t = 14
2t2 + 7t - 9 = 0
t1 = -9/2 и t2 = 1
lgx = -9/2 lgx =1
По определения логарифма выражаем x:
Область определения уравнения x>0
Оба корня удовлетворяют области определения уравнения
Слайд 48
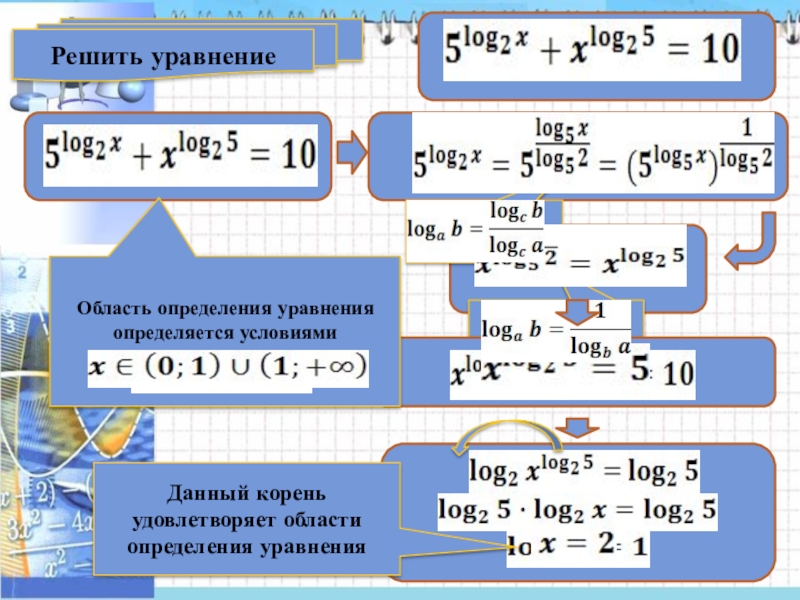
Решить уравнение
Область определения уравнения определяется условиями
Данный корень удовлетворяет области определения уравнения
Слайд 49
Уравнения – это золотой ключ, открывающий все математические сезамы
С. Коваль
Источники
Алгебра и
Соболь Б. В., Виноградова И. Ю., Рашидова Е. В. Пособие для подготовки к ЕГЭ и централизованному тестированию по математике. Изд. 3-е. – Р н/Д: «Феникс», 2003. – 352 с.
http://edu.nstu.ru/courses/dovuz/urner/demo/Log/Teor/Fru_m.htm
http://www.math.md/school/praktikum/logr/logr.html
Слайд 50Учебно-исследовательский проект
«Логарифмы в ЕГЭ
и не только…»
УЧЕНИЦА 11РН КЛАССА
МКОУ СОШ №32
УЧИТЕЛЬ МАТЕМАТИКИ
Оршокдугова Р.М.
Слайд 52Проблема
Дефицит методов решения экзаменационных логарифмических неравенств, предлагаемых в С3.
Ответ на
Слайд 53
Исследование механизма решения задач С3 при помощи нестандартных методов
Выявление интересных фактов логарифмов
Слайд 54План работы
Подборка математической литературы по теме исследования.
Отбор задач
Составление сборника задач и презентации «Логарифмы вокруг нас».
Письменное оформление исследовательской работы.
Выполнение презентации к выступлению на конференции.
Слайд 55 История вопроса
Слово логарифм происходит от
Ежели под геометрическою прогрессиею, начинающеюся с единицы, подписана будет арифметическая прогрессия, начинающаяся с нуля, то числа, внизу подписанные, называются для верхних – логарифмы.
Положим, что даны прогрессии:
геом. 1, 2, 4, 8, 16, 32, 64, 128, 256,
арифм. 0, 1, 2, 3, 4, 5, 6, 7, 8.
Тогда логарифм 1 будет 0;
логарифм 4 будет 2;
а логарифм 32 будет 5 и проч.»
Джон Непер
(Шотландия, 17 век)
Слайд 56 Проектный продукт
Сборник
«
Презентация
«Логарифмы вокруг нас»
Слайд 57Методы решения уравнений
Равносильные переходы и обобщённый метод интервалов
Метод рационализации
Нестандартная подстановка
Задания с
Слайд 60 Содержание презентации
«Логарифмы вокруг нас»
Логарифмическая спираль
Звёзды и логарифмы
Шумы и
Живопись и логарифмы
Слайд 62Логарифмы и живопись
Логарифмические линии в природе замечают не
Слайд 63 Выводы
Поставленная
Гарантией успеха при создании исследовательского проекта для меня стали: значительный школьный опыт, умение добывать информацию из различных источников, проверять ее достоверность, ранжировать ее по значимости.
Кроме непосредственно предметных знаний по математике, расширила свои практические навыки в области информатики, получила новые знания и опыт в области психологии, наладила контакты с одноклассниками, научилась сотрудничать с взрослыми людьми. В ходе проектной деятельности развивались организационные, интеллектуальные и коммуникативные общеучебные умения и навыки.
Слайд 64 Использованная литература
1. Корянов А. Г. ,Прокофьев А. А. Системы неравенств
2. Малкова А. Г. Подготовка к ЕГЭ по математике.
3. Самарова С. С. Решение логарифмических неравенств.
4. Математика. Сборник тренировочных работ под редакцией А.Л. Семёнова и И.В. Ященко. -М.: МЦНМО, 2009. - 72 с.-
5 Математика . Тематические тесты. Часть 2. Подготовка к ЕГЭ -2010.10-11 классы /
Ф. Ф. Лысенко. — Ростов-на-Дону: Легион, 2009. — 176 с. — (Готовимся к ЕГЭ )
6.Самое полное издание типовых вариантов реальных заданий ЕГЭ : 2010: Математика /авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.;
7. Ященко И. В., Шестаков С. А., Захаров П. И. Подготовка к ЕГЭ по математике в 2010 году. Методические рекомендации.
8.Универсальные материалы для подготовки учащихся / ФИПИ — М: Интеллект-Центр, 2010. — 96 с. (Под редакцией А. Л. Семенова и И. В. Ященко)
9. Сайт Дмитрия Гущина «РЕШУ ЕГЭ»