- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа Решение практических задач по теории вероятностей
Содержание
- 1. Презентация по алгебре и началам анализа Решение практических задач по теории вероятностей
- 2. Задача 1. Две фабрики выпускают одинаковые лампочки.
- 3. Задача 1.(продолжение) Две фабрики выпускают одинаковые лампочки.
- 4. Задача 2.Два завода выпускают одинаковые автомобильные предохранители.
- 5. Задача 3.На тренировку пришел 21 школьник, среди
- 6. (продолжение)Теперь найдем РА1(А2) то есть условную вероятность
- 7. Задача 5 В классе 21 шестиклассник, среди
- 8. Задача 6. В случайном эксперименте симметричную монету
- 9. Задача 7. В Волшебной стране бывает два
- 10. Задача 8. В Волшебной стране бывает два
- 11. Задача 9. В торговом центре два одинаковых
- 12. Задача 10. Вероятности поражения цели первым и
- 13. Задача 11Перед началом первого тура чемпионата по
- 14. ПродолжениеИтак, вероятность того, что Василий Зайцев окажется
- 15. Слайд 15
- 16. =
- 17. Ответ: .
- 18. Задание 17. Из ящика, в котором лежат фломастеры,
- 19. Задача 18Павел Иванович совершает прогулку из точки
- 20. Задача 20. Артём гуляет по парку. Он выходит
- 21. Событие A - в автобусе меньше 15
- 22. Задача 21За круглый стол на 101 стул
- 23. Используемая литература:Задачи открытого банка заданий ЕГЭ
Слайд 1Путилина Ж.Н.
БОУ СОШ №3, 09.01.2019
Подготовка к ЕГЭ
Решение задач по теории вероятностей
Задача:
№10
№4 (профильный уровень)
Слайд 2Задача 1. Две фабрики выпускают одинаковые лампочки. Первая фабрика выпускает 60% лампочек,
Слайд 3Задача 1.(продолжение) Две фабрики выпускают одинаковые лампочки. Первая фабрика выпускает 60% лампочек,
Вероятность того, что лампочки выпущены на первой фабрике и они бракованные: 0,03∙0,6=0,018 .
Вероятность того, что лампочки выпущены на второй фабрике и они бракованные : 0,02∙ 0,4 = 0,008.
Поэтому по формуле полной вероятности вероятность того, что случайно купленная в магазине лампочка окажется дефектной. : 0,018 + 0,008 = 0,026
Ответ: 0,026.
Слайд 4Задача 2.
Два завода выпускают одинаковые автомобильные предохранители. Первый завод выпускает 40%
Решение:
По условию задачи первый завод выпускает 40% предохранителей из 100%. Другими словами он выпускает 40/100 = 4/10=0,4 доли от общего производства двух заводов. Второй завод аналогично выпускает 60% = 60/100 = 6/10=0,6 доли от общего числа деталей.
Среди этих 4/10 по условию 4% брака, что значит 4/100 от 4/10, это равно: 4/100 * 4/10 = 16/1000=0,016. То есть от всего объема выпущенных деталей 0.016 бракованных выпускает первый завод.
Аналогично найдем долю брака со второго завода: 3/100 * 6/10 = 18/1000=0,018.
Всего бракованных деталей с обоих заводов будет:
0,016 + 0,018 = 0,034. Это и будет равно вероятности того, что случайно выбранный в магазине предохранитель окажется бракованным.
Ответ: 0,034.
Слайд 5Задача 3.
На тренировку пришел 21 школьник, среди них два брата -
Решение: Нас устроит, если Василий и Павел окажутся в любой из трех команд.
Допустим, событие А - оба попали в 1-ю футбольную команду
событие В - оба попали во 2-ю футбольную команду
событие С - оба попали в 3-ю футбольную команду.
Эти события несовместны и любое из них нас устроит. Найдем Р(А+В+С) = Р(А)+Р(В)+Р(С).
В свою очередь событие А состоит из двух зависимых событий:
А1 - что Василий окажется в 1-ой футбольной команде
А2 - что Павел окажется в 1-ой футбольной команде, ⇔
Р(А) = Р(А1) * РА1(А2).
Вероятность, что Василий попадет в 1-ю футбольную команду Р(А1): m=1, так как один благоприятный исход, а n=3, так как всего возможно три исхода.
Поэтому Р(А1) = 1/3.
Слайд 6(продолжение)
Теперь найдем РА1(А2) то есть условную вероятность того, что Павел попадет в
Число благоприятных условий равно 6, так как одно место в команде уже занято Василием (то есть нас устраивает, если Павел попадет в любое из шести свободных мест в команде и m=6), а общее число всех исходов = 20, так как Василий уже не участвует в выборке (то есть всего претендентов осталось 20 человек и n=20).
Поэтому РА1(А2) = 6/20 = 3/10
Таким образом Р(А) = 1/3 ∙ 3/10 = 1/10.
Аналогично рассуждая, найдем Р(В) = 1/10 и Р(С) = 1/10.
Поэтому Р(А+В+С) = 1/10 + 1/10 + 1/10 = 3/10 = 0,3.
Ответ: 0,3.
Слайд 7Задача 5
В классе 21 шестиклассник, среди них два друга —
Решение.
Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся одноклассников, а остальные 14 будут в других группах. Вероятность того, что второй друг окажется среди этих 14 человек, равна 14 : 20 = 0,7.
Ответ: 0,7.
Слайд 8Задача 6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность
А) что наступит исход РОР (в первый и третий разы выпадает решка, во второй — орёл).
Б) что выпадет хотя бы две решки. (РР)
Решение.
Всего возможных исходов — восемь. Двоичный код.
Обозначим 1-решка, 0-орел.
А) Благоприятным является один: решка-орел-решка.
Следовательно, искомая вероятность равна
1 : 8 = 0,125. Ответ: 0,125
Б) Благоприятными являются четыре: решка-решка-решка, решка-решка-орел, решка-орел-решка, орел-решка-решка. Следовательно, искомая вероятность равна 4 : 8 = 0,5.
Ответ: 0,5.
Слайд 9Задача 7. В Волшебной стране бывает два типа погоды: хорошая и
Решение. Рассмотрим всевозможные случаи. Пусть 0-отличная погода, 1-хорошая погода.
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) =
=0,128 + 0,128 + 0,008 + 0,128 = 0,392.
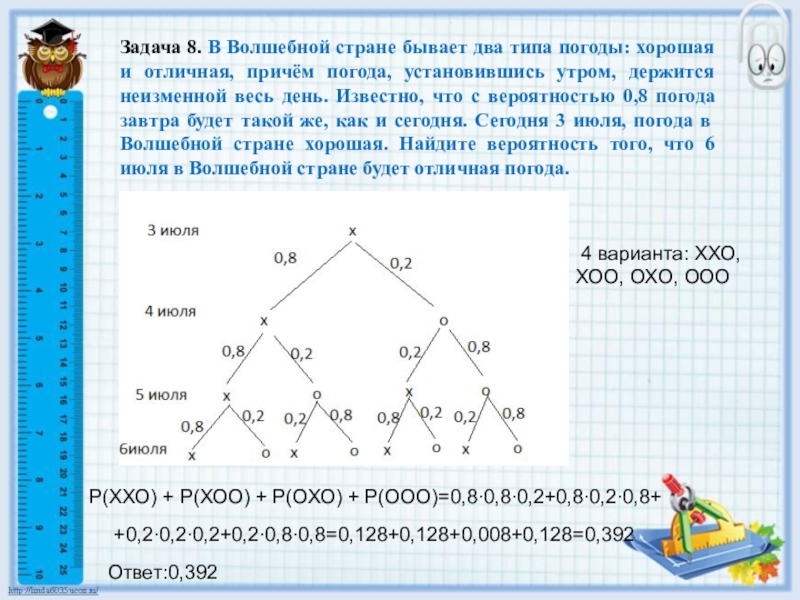
Слайд 10Задача 8. В Волшебной стране бывает два типа погоды: хорошая и
4 варианта: ХХО, ХОО, ОХО, ООО
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО)=0,8∙0,8∙0,2+0,8∙0,2∙0,8+
+0,2∙0,2∙0,2+0,2∙0,8∙0,8=0,128+0,128+0,008+0,128=0,392
Ответ:0,392
Слайд 11Задача 9. В торговом центре два одинаковых автомата продают кофе. Вероятность
А – кофе закончится в первом автомате; В – кофе закончится во втором автомате.
По условию задачи,
отметим, что эти события не являются независимыми, в противном случае
Вероятность противоположного события «кофе останется в обоих автоматах» равна
Ответ:0,52
Слайд 12Задача 10. Вероятности поражения цели первым и вторым орудиями равны, соответственно,
Решение. Поскольку вероятности поражения цели орудиями (события А и В соответственно) не зависят от результатов стрельбы каждого из напарников, то эти события независимы. Искомая вероятность рассчитывается по формуле
Р(А + В) = Р(А) + Р(В) -Р(А)Р(В) = 0,8 + 0,9 - 0,72 = 0,98.
В случае полной группы событий Alt A2, ..., А„ сумма их вероятностей равна единице:
P(At) + P(A2) + + P(A) = 1.
Другое условие задачи : Оба орудия поразят цель
Р(А * В) = Р(А) * Р(В)=0,8 * 0,9 =0,72
Слайд 13Задача 11
Перед началом первого тура чемпионата по шахматам участников разбивают на
Решение:
В первом туре участвуют 16 шахматистов, они разбиты на пары. Всего пар 8 (16:2=8).
Допустим, Василий Зайцев окажется в первой паре шахматистов. Вероятность этого найдем по определению вероятности: 2/16 = 1/8.
Вероятность того, что вторым окажется россиянин посчитаем тоже по определению вероятности: 3/15 = 1/5 (так как благоприятных исходов - 3, а всего возможно исходов 15, так как Василий уже выбран).
1) Вероятность события А - это отношение числа исходов, благоприятствующих его наступлению к числу всех исходов (несовместных, единственно возможных и равновозможных). Р(А)= m/n, где m - число благоприятных исходов, а n - число всех исходов.
Значит, вероятность того, что Василий Зайцев окажется с россиянином в паре будет равна
1/8 * 1/5 = 1/40 =0,025(по формуле поиска вероятности произведения событий).
2) Теорема: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило: Р(А*В) = Р(А) * РА(В).)
Слайд 14Продолжение
Итак, вероятность того, что Василий Зайцев окажется с россиянином в паре
1/8 * 1/5 = 1/40 =0,025(по формуле поиска вероятности произведения событий).
Но заметим, что нас устроило бы, что Василий будет в любой из 8 пар вместе со вторым россиянином. Поэтому искомая вероятность будет равна: 1/40 + 1/40 + 1/40+ 1/40+ 1/40+ 1/40 + 1/40+ 1/40 = 1/40 * 8 = 1/5 = 0,2 (по формуле поиска вероятности суммы несовместных событий)
4) Теорема: Вероятность суммы несовместных событий А и В равна сумме вероятностей этих событий Р(А+В) = Р(А)+Р(В).
Ответ: 0,2.
Слайд 18Задание 17. Из ящика, в котором лежат фломастеры, не глядя достали два
Решение.
Изначально в ящике 12+13=25 фломастеров. При выборе первого фломастера вероятность того, что он будет синего цвета, равна 12/25. Если первый выбранный фломастер действительно оказался синего цвета, то в ящике остается 24 фломастера и из них 11 синих. Поэтому вероятность выбора второго синего фломастера, равна 11/24. Так как и первый и второй фломастеры должны быть синими, получаем произведение этих вероятностей:
Рассмотрим вторую ситуацию, когда оба фломастера могут быть красными.
Подобными рассуждениями получаем вероятность
Так как нас интересует наступление или первого или второго исхода (при несовместности этих событий), получаем значение искомой вероятности:
Ответ: 0,48.
Слайд 19Задача 18
Павел Иванович совершает прогулку из точки А по дорожкам парка.
Решение:
Теорема: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:
Р(А*В) = Р(А) * РА(В).)
Ответ: 0,125.
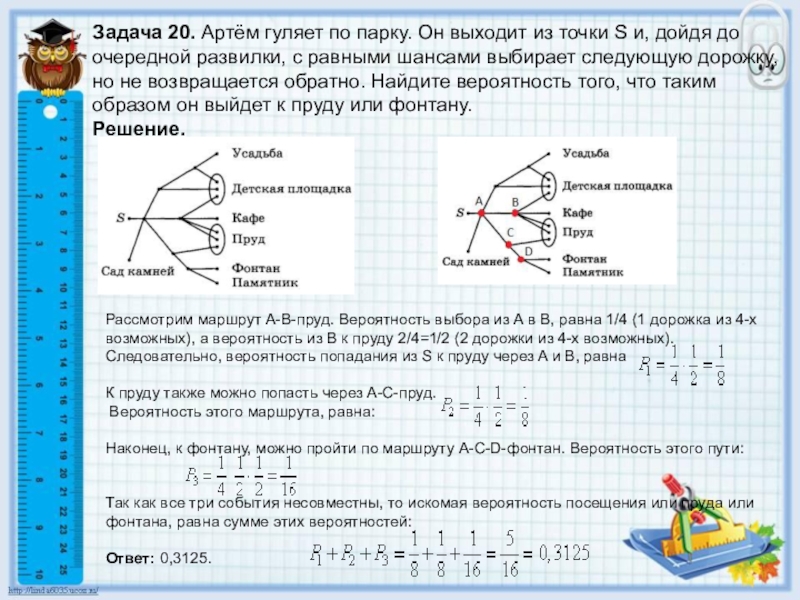
Слайд 20Задача 20. Артём гуляет по парку. Он выходит из точки S и,
Решение.
Рассмотрим маршрут A-B-пруд. Вероятность выбора из A в B, равна 1/4 (1 дорожка из 4-х возможных), а вероятность из В к пруду 2/4=1/2 (2 дорожки из 4-х возможных). Следовательно, вероятность попадания из S к пруду через A и B, равна
К пруду также можно попасть через A-C-пруд.
Вероятность этого маршрута, равна:
Наконец, к фонтану, можно пройти по маршруту A-C-D-фонтан. Вероятность этого пути:
Так как все три события несовместны, то искомая вероятность посещения или пруда или фонтана, равна сумме этих вероятностей:
Ответ: 0,3125.
Слайд 21Событие A - в автобусе меньше 15 пассажиров
Событие В -
Событие A + B - в автобусе меньше 20 пассажиров
События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
P(В) = 0,94 − 0,56 = 0,38.
Ответ:0,38
Слайд 22Задача 21
За круглый стол на 101 стул в случайном порядке рассаживаются
Решение.
Пусть первой за стол сядет девочка, тогда для каждого из оставшихся ребят (в том числе и для второй девочки ) вероятность оказаться на любом из оставшихся стульев равна А мест, удовлетворяющих условию задачи, только
два. Таким образом вероятность, что между двумя девочками будет сидеть один мальчик равна
Ответ 0,02
Слайд 23Используемая литература:
Задачи открытого банка заданий ЕГЭ по математике 2019.
2. В.
3. «ЕГЭ, математика 2019г.», И.В. Ященко (базовый, профильный уровень).
4. Интернет – ресурсы.
5. Д.Д. Гущин, Решу ЕГЭ, 2019г.