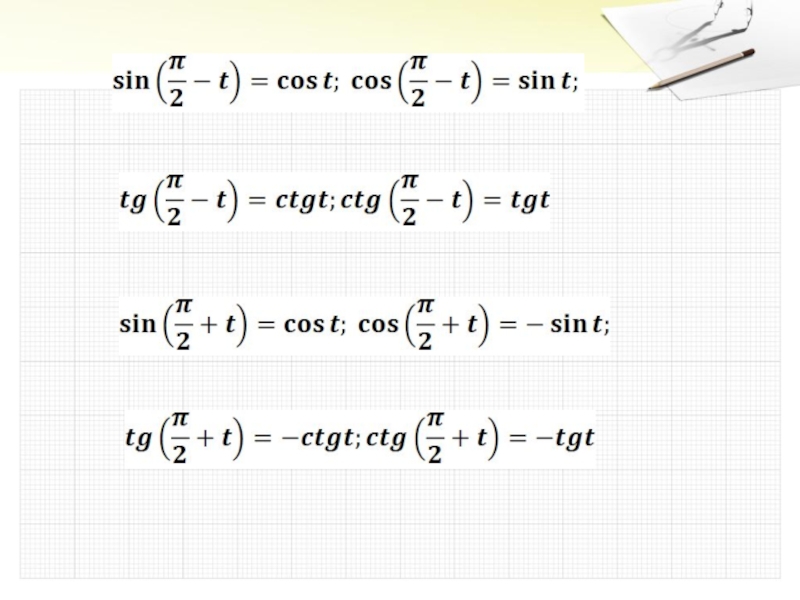- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа на тему Формулы приведения (10 класс)
Содержание
Любое выражение вида , где n – произвольное целое число, можно привести к более простому виду, при котором под знаком тригонометрической функции будет содержаться только аргумент t.
Слайд 1Тригонометрические функции
Формулы приведения
Нигматуллин Радий Радиевич
МБОУ СШ №24 а. Шенджий,
Республика Адыгея
Слайд 2Любое выражение вида , где
n – произвольное целое число, можно привести к более простому виду, при котором под знаком тригонометрической функции будет содержаться только аргумент t.
Слайд 7Алгоритм формул приведения
Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов
вида π-t, π+t, 2π-t, 2π+t, то наименование тригонометрической функции сохраняется.
Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π/2-t, π.2+t, 3π/2-t, 3π/2+t, то наименование тригонометрической функции изменяется на кофункцию (sin <−> cos, tg <−> ctg).
Перед полученной функцией аргумента t надо поставить тот знак, который имеет преобразуемая функция по положению ее на единичной окружности.
Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π/2-t, π.2+t, 3π/2-t, 3π/2+t, то наименование тригонометрической функции изменяется на кофункцию (sin <−> cos, tg <−> ctg).
Перед полученной функцией аргумента t надо поставить тот знак, который имеет преобразуемая функция по положению ее на единичной окружности.