- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа на тему ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ и НЕРАВЕНСТВА
Содержание
- 1. Презентация по алгебре и началам анализа на тему ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ и НЕРАВЕНСТВА
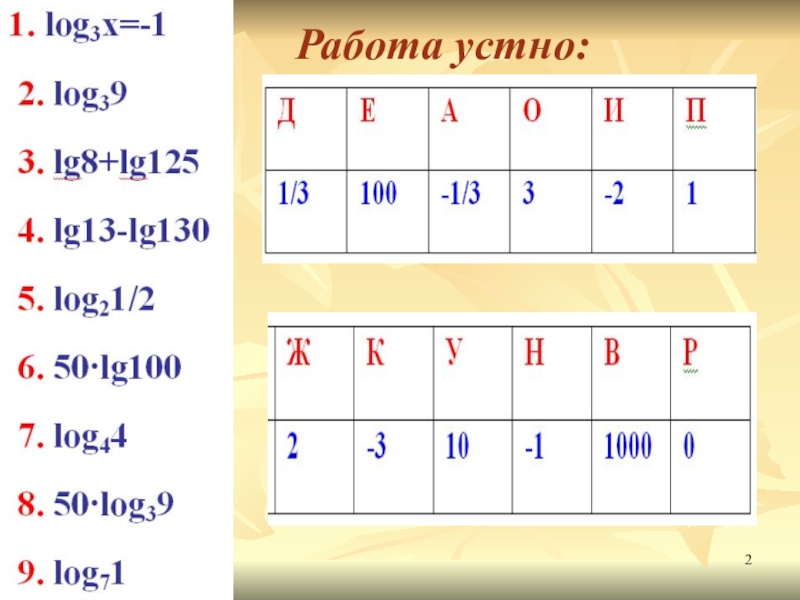
- 2. Работа устно:
- 3. Джон НЕПЕР (1550 - 1617)Известный шотландский
- 4. повторить свойства логарифма и логарифмической функциипознакомиться с
- 5. Определение логарифма. Логарифмом положительного числа b по
- 6. ЗАПОМНИ !Сладкая парочка!Два в одном!Два берега у
- 7. Работа у доски по карточкам с проверкой
- 8. Работа у доски по карточкам с проверкой
- 9. xy01231248- 1- 2График функции y = loga
- 10. Слайд 10
- 11. Задание №1Найдите наибольшее и наименьшее значения функции
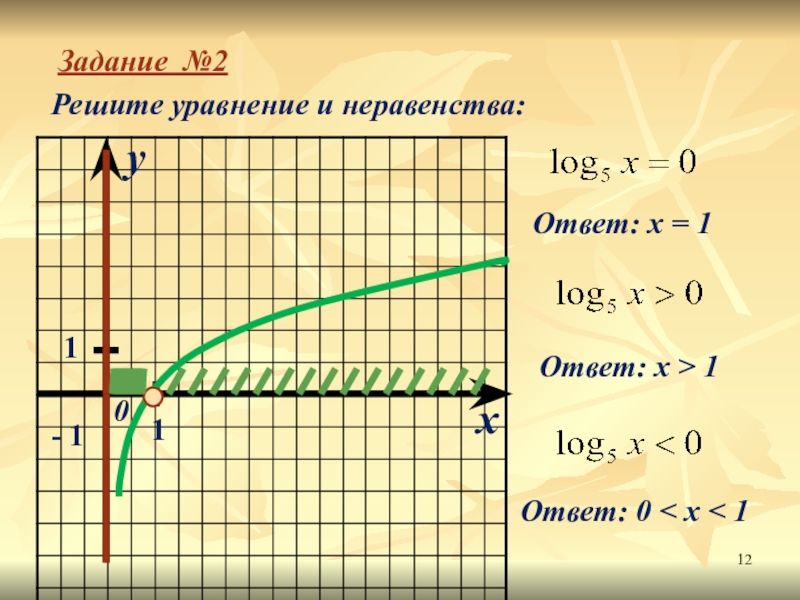
- 12. Задание №2Решите уравнение и неравенства:xy011- 1 Ответ:
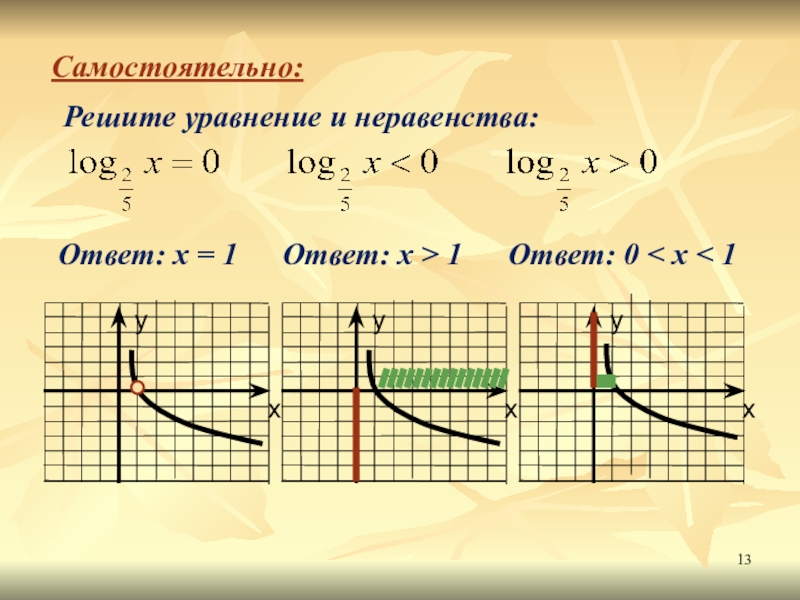
- 13. Самостоятельно:Решите уравнение и неравенства:Ответ: х = 1Ответ: х > 1Ответ: 0 < х < 1
- 14. Слайд 14
- 15. В записанных формулах найти и исправить ошибки
- 16. Решите логарифмические уравнения: Работа в группах1)
- 17. Решение логарифмических уравнений: 1) log2
- 18. Решение логарифмических уравнений: 2) lg
- 19. Решение логарифмических уравнений: 3) lg
- 20. Решение логарифмических уравнений: 4) Log x
- 21. Слайд 21
- 22. Слайд 22
- 23. повторить свойства логарифма и логарифмической функциипознакомиться с
- 24. Слайд 24
- 25. Домашнее задание§44-45№ 44.13(а,б), № 44.17(в), № 45.11(в,г)
- 26. Вот вы когда-нибудь слыхалиО логарифмической спирали?
- 27. По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника
- 28. По логарифмической спирали свёрнуты раковины многих улиток и моллюсков.
- 29. По логарифмическим спиралям выстраиваются рога многих животных
- 30. По логарифмической спирали формируется тело циклона
- 31. Даже пауки, сплетая паутину, закручивают нити вокруг центра по логарифмической спирали.
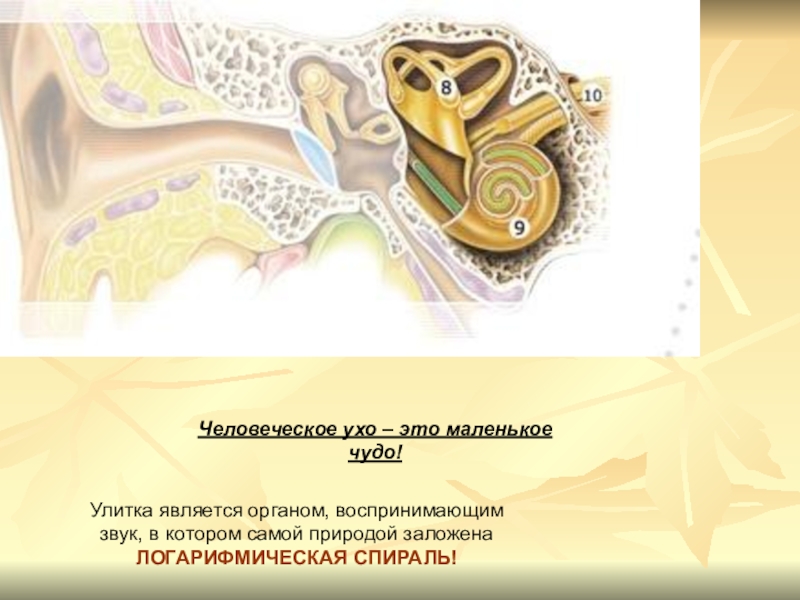
- 32. Улитка является органом, воспринимающим звук, в котором самой природой заложенаЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ!Человеческое ухо – это маленькое чудо!
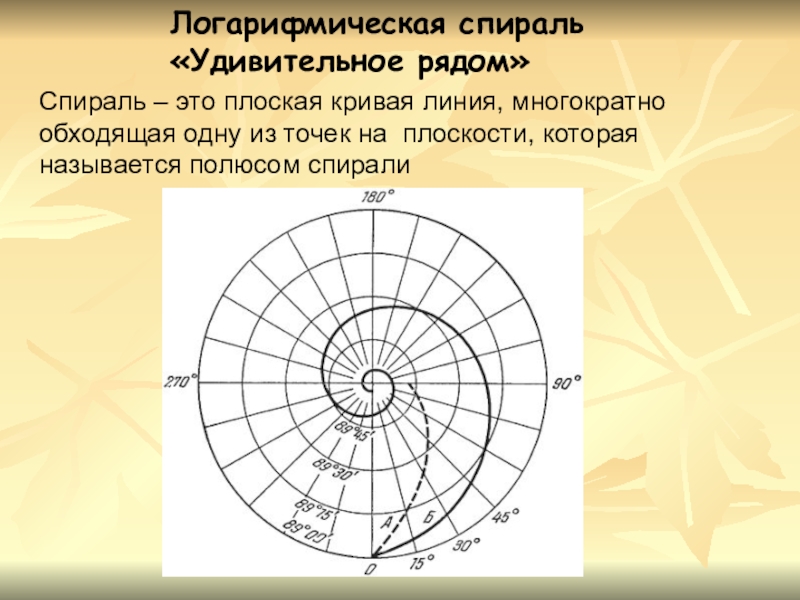
- 33. Логарифмическая спираль «Удивительное рядом»Спираль – это
Работа устно:
Слайд 3
Джон НЕПЕР (1550 - 1617)
Известный шотландский математик,
вошел в историю
математики как изобретатель
логарифмов, он составитель первой
таблицы логарифмов, которой посвятил
20 лет своей жизни.
Свой знаменитый труд
“Описание удивительных таблиц
логарифмов” опубликовал
лишь в 1614 году.
логарифмов, он составитель первой
таблицы логарифмов, которой посвятил
20 лет своей жизни.
Свой знаменитый труд
“Описание удивительных таблиц
логарифмов” опубликовал
лишь в 1614 году.
Слайд 4
повторить свойства логарифма и логарифмической функции
познакомиться с историей логарифмов и их
использованием в деятельности человека и в природе
применять полученные знания при выполнении практических заданий
проверять правильность полученных решений
Цели урока
Слайд 5Определение логарифма.
Логарифмом положительного числа b по положительному и отличному от
1 основанию a - называют показатель степени, в которую нужно возвести число a, что бы получить число b
Слайд 6
ЗАПОМНИ !
Сладкая парочка!
Два в одном!
Два берега у одной реки!
Два сапога –
пара!
Близки и неразлучны!
Нам не жить
друг без
друга!
Логарифм и ОДЗ
вместе
трудятся
везде!
ОН
- ЛОГАРИФМ!
ОНА
-
ОДЗ!
Слайд 7Работа у доски по карточкам с проверкой на экране
Решение:
По определению
логарифма:
4+x=5^2
4+x=25
x=21
Ответ: x = 21.
Ответ: x = 21.
Решение:
По определению логарифма:
8+x=2^3
8+x=8
x=0
Ответ: x = 0.
Слайд 8Работа у доски по карточкам с проверкой на экране
Решение:
По определению
логарифма:
9+x=3^4
9+x=81
x=72
Ответ: x = 72.
Ответ: x = 72.
Решение:
По определению логарифма:
3+x=2^7
3+x=128
x=125
Ответ: x = 125.
Слайд 9x
y
0
1
2
3
1
2
4
8
- 1
- 2
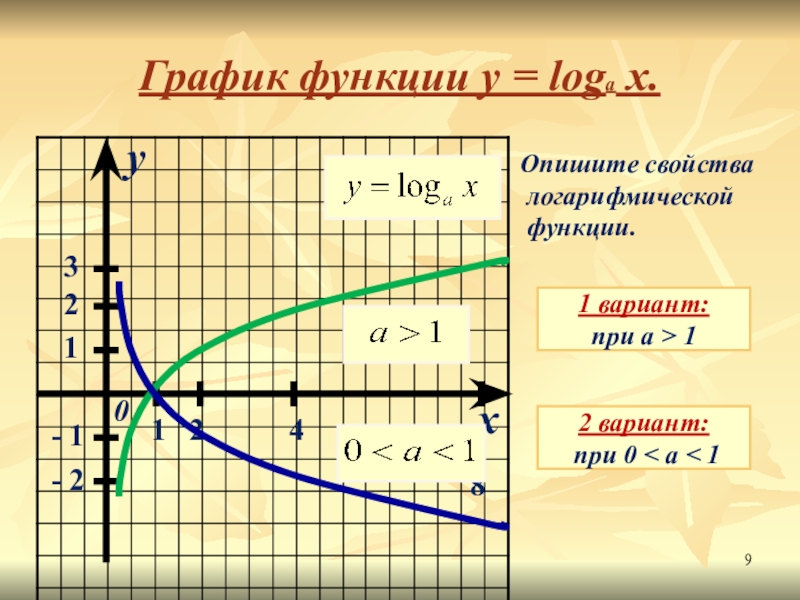
График функции y = loga x.
Опишите свойства
логарифмической
функции.
1 вариант:
при a > 1
2 вариант:
при 0 < a < 1
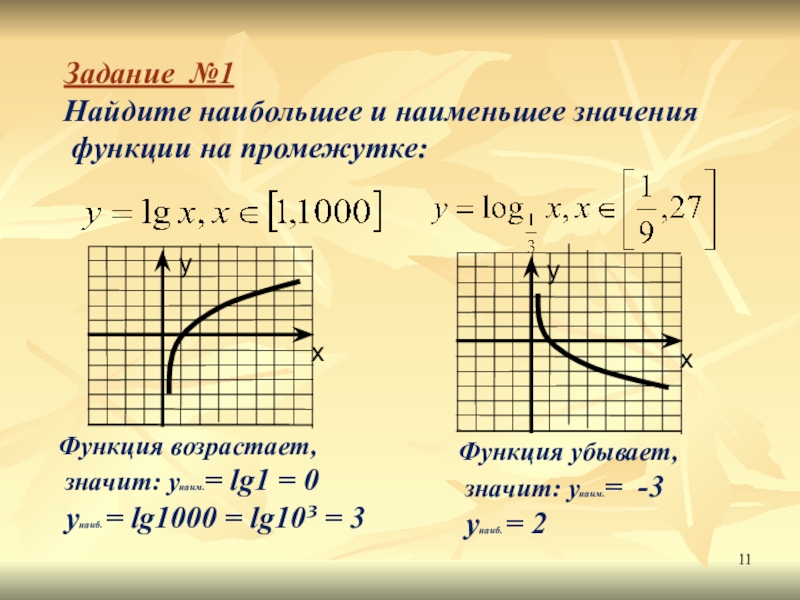
Слайд 11Задание №1
Найдите наибольшее и наименьшее значения
функции на промежутке:
Функция возрастает,
значит:
yнаим.= lg1 = 0
yнаиб. = lg1000 = lg10³ = 3
yнаиб. = lg1000 = lg10³ = 3
Функция убывает,
значит: yнаим.= -3
yнаиб. = 2
Слайд 16Решите логарифмические уравнения:
Работа в группах
1) log2 (2+log3 (3+x) )= 0
2) lg(3x-2)-1/2lg(x+2)=2-lg50
3) lg 2 x-5lgx+6=0
4) logх4+logХ264=5
Слайд 17Решение логарифмических уравнений:
1) log2 (2+log3 (3+x) )= 0
Решение:
2+ log3 (3+x) =1 ОДЗ: 3+x>0,
log3( 3+x)= -1 2+log3 (3+x)> 0
3+x= 1\3
x= -2 2\3
Ответ: -2 2\3
Слайд 18Решение логарифмических уравнений:
2) lg (3x -2) - lg√(x+2)=lg100 –
lg50
lg (3x-2)\ √(x+2) = lg 2
(3x-2)\ √(x+2) = 2
(3x-2)= 2 √(x+2)
9х2 - 16х --4= 0
D = 400,
х1= 2, х2= -2\9 - посторонний корень
ОДЗ : 3x-2>0, x+2>0
Ответ: 2
lg (3x-2)\ √(x+2) = lg 2
(3x-2)\ √(x+2) = 2
(3x-2)= 2 √(x+2)
9х2 - 16х --4= 0
D = 400,
х1= 2, х2= -2\9 - посторонний корень
ОДЗ : 3x-2>0, x+2>0
Ответ: 2
Слайд 19Решение логарифмических уравнений:
3) lg 2 x-5lgx+6=0
lg x = t
t2 - 5t + 6 = 0 t1 = 2 t2= 3
lg x = 2 lg x = 3
x= 100 x= 1000
ОДЗ : x>0,
Ответ: 100, 1000.
t2 - 5t + 6 = 0 t1 = 2 t2= 3
lg x = 2 lg x = 3
x= 100 x= 1000
ОДЗ : x>0,
Ответ: 100, 1000.
Слайд 20Решение логарифмических уравнений:
4) Log x 4+1\2log X 64 =5
log x 32 = 5
x=2
ОДЗ x> 0, X≠1
Ответ:2.
x=2
ОДЗ x> 0, X≠1
Ответ:2.
Слайд 23
повторить свойства логарифма и логарифмической функции
познакомиться с историей логарифмов и их
использованием в деятельности человека и в природе
применять полученные знания при выполнении практических заданий
проверять правильность полученных решений
Цели урока
Слайд 24
Рефлексия
1. Сегодня на уроке я узнал… 2. Было интересно… 3. Было трудно… 4. Я выполнял задания… 5. Я понял, что… 6. Теперь я могу… 7. Я почувствовал, что… 8. Я приобрел… 9. Я научился… 10. У меня получилось… 11. Я смог… 12. Я попробую… 13. Меня удивило 14. Мне захотелось… 15. Урок дал мне для жизни…
1. Сегодня на уроке я узнал… 2. Было интересно… 3. Было трудно… 4. Я выполнял задания… 5. Я понял, что… 6. Теперь я могу… 7. Я почувствовал, что… 8. Я приобрел… 9. Я научился… 10. У меня получилось… 11. Я смог… 12. Я попробую… 13. Меня удивило 14. Мне захотелось… 15. Урок дал мне для жизни…
Слайд 32Улитка является органом, воспринимающим звук, в котором самой природой заложена
ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ!
Человеческое
ухо – это маленькое чудо!
Слайд 33Логарифмическая спираль
«Удивительное рядом»
Спираль – это плоская кривая линия, многократно обходящая
одну из точек на плоскости, которая называется полюсом спирали
