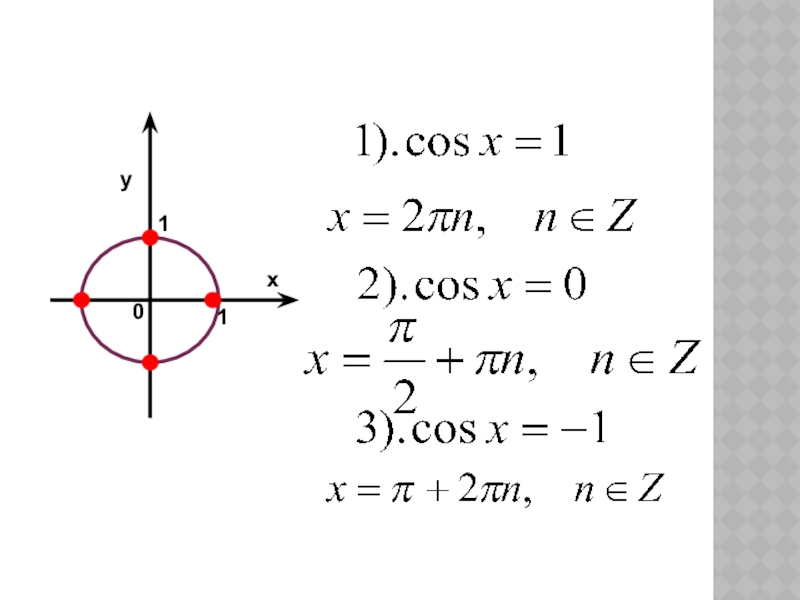- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа 11 класс по темеТригонометрия
Содержание
- 1. Презентация по алгебре и началам анализа 11 класс по темеТригонометрия
- 2. ТРИГОНОМЕТРИЯТригонометрия-это часть геометрии, где с помощью тригонометрических
- 3. ЭТАПЫ РАЗВИТИЯ ТРИГОНОМЕТРИИТригонометрия в древности являлась вспомогательным
- 4. ОПРЕДЕЛЕНИЕ SIN,COS,TG,CTGСинусом угла α называется отношение ординаты
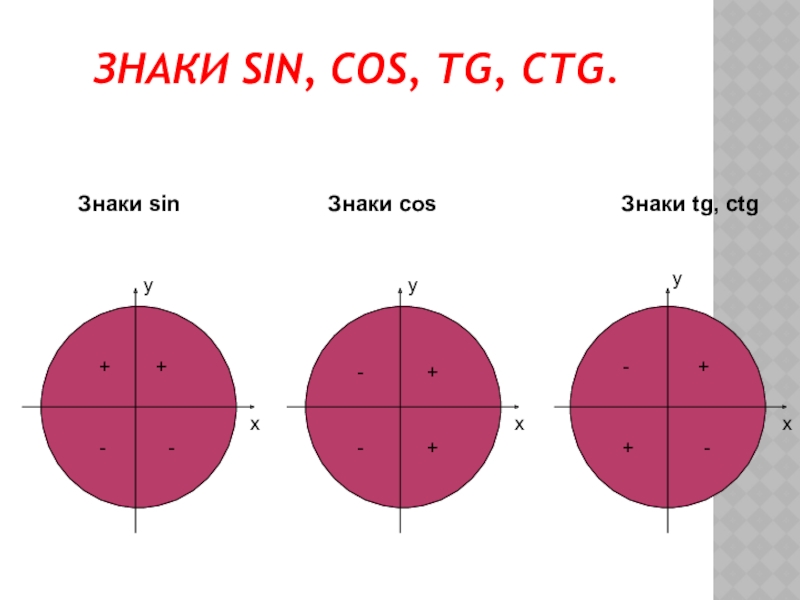
- 5. ЗНАКИ SIN, COS, TG, CTG.xxxyyyЗнаки sin
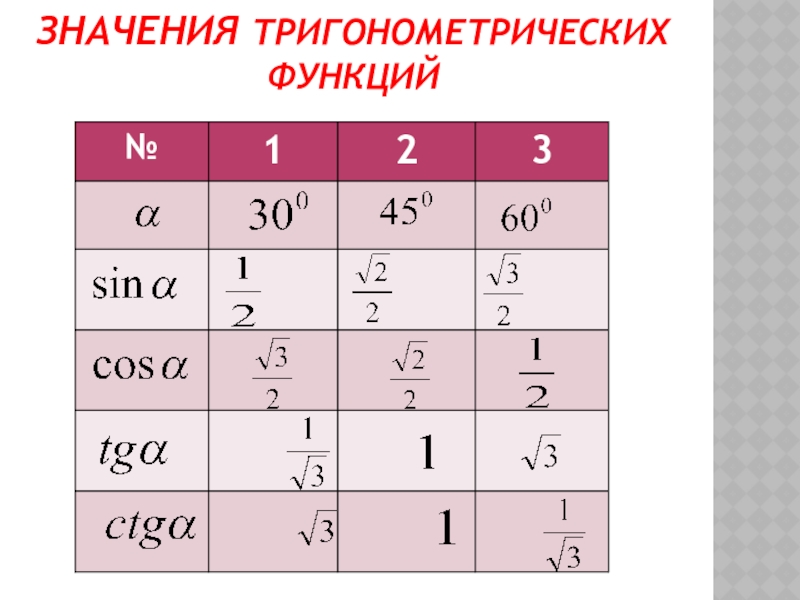
- 6. ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
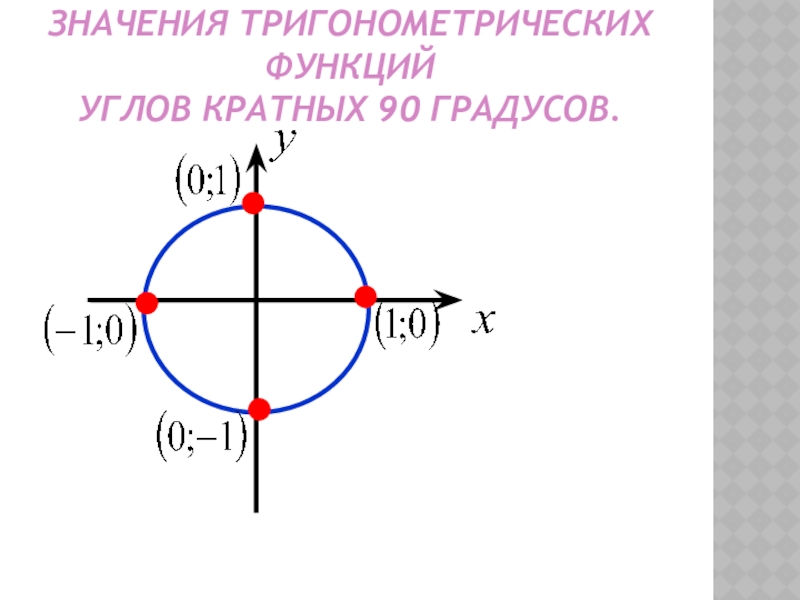
- 7. ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙУГЛОВ КРАТНЫХ 90 ГРАДУСОВ.
- 8. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА sin² α + cos²
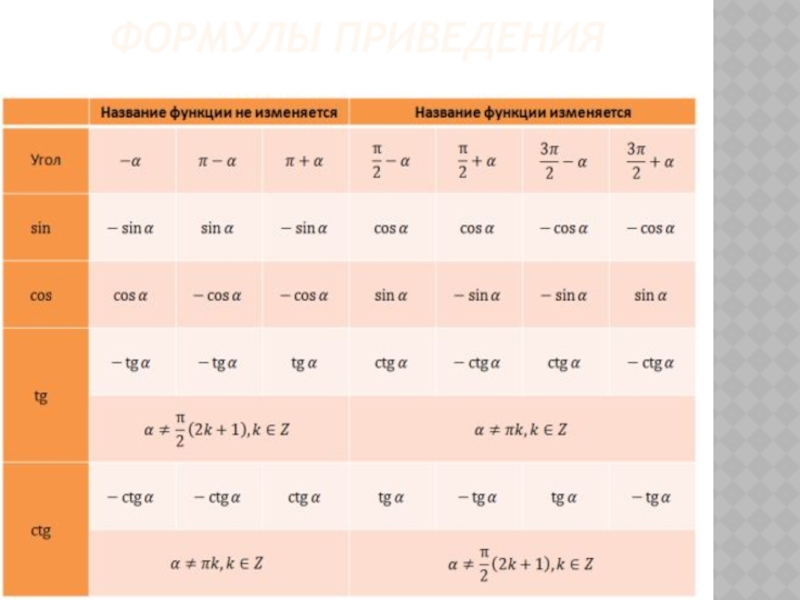
- 9. ФОРМУЛЫ ПРИВЕДЕНИЯ
- 10. ФОРМУЛЫ СЛОЖЕНИЯsin (α + β) = sin
- 11. ФОРМУЛЫ ДВОЙНОГО УГЛАcos 2α = cos² α
- 12. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИИЙ
- 13. УРАВНЕНИЯcost = asint = a
- 14. ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
- 15. УРАВНЕНИЕ COST = A0xy2. Отметить точку а
- 16. УРАВНЕНИЕ SINT = A0xy2. Отметить точку а
- 17. ЧАСТНЫЕ СЛУЧАИ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ 11ху0
- 18. 11ху0
- 19. 0ху01-1
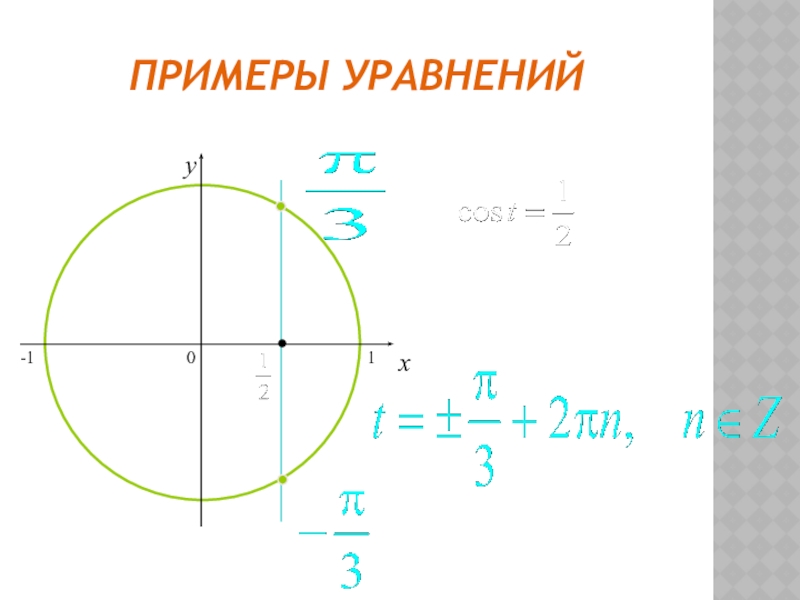
- 20. ПРИМЕРЫ УРАВНЕНИЙ0xy-11
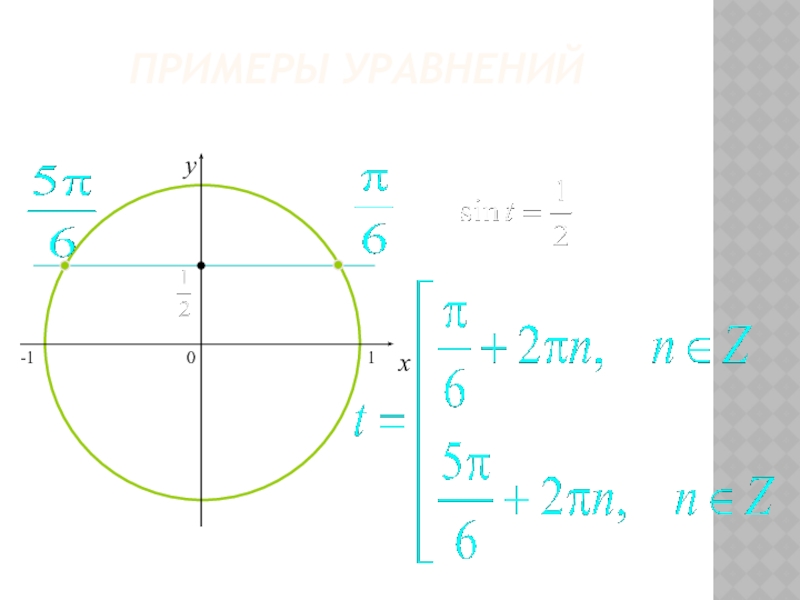
- 21. ПРИМЕРЫ УРАВНЕНИЙ0xy-11
- 22. НЕРАВЕНСТВАcost >a, cost ≤ a sint >a, sint ≤ a
- 23. НЕРАВЕНСТВО COST > A0xy1. Отметить на оси
- 24. НЕРАВЕНСТВО COST ≤ A0xy1. Отметить на оси
- 25. НЕРАВЕНСТВО SINT > A0xy1. Отметить на оси
- 26. НЕРАВЕНСТВО SINT ≤ A0xy1. Отметить на оси
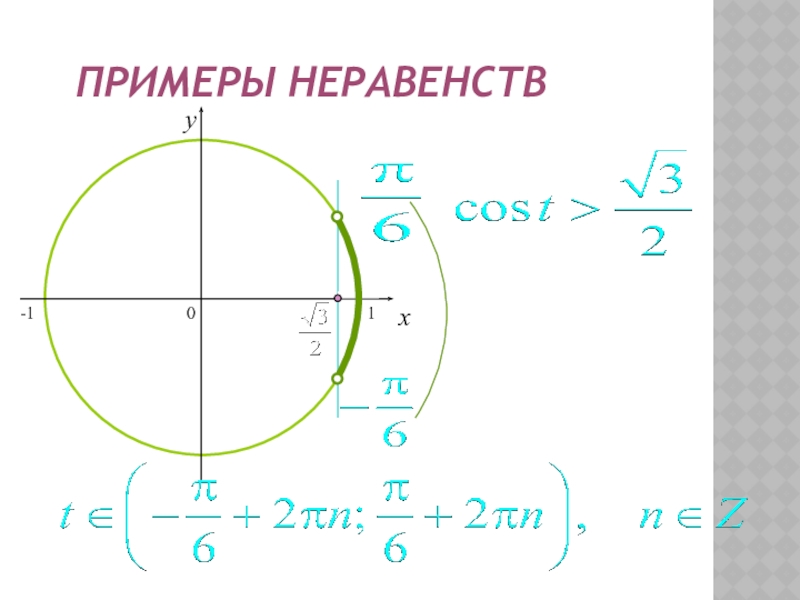
- 27. ПРИМЕРЫ НЕРАВЕНСТВ0xy-11
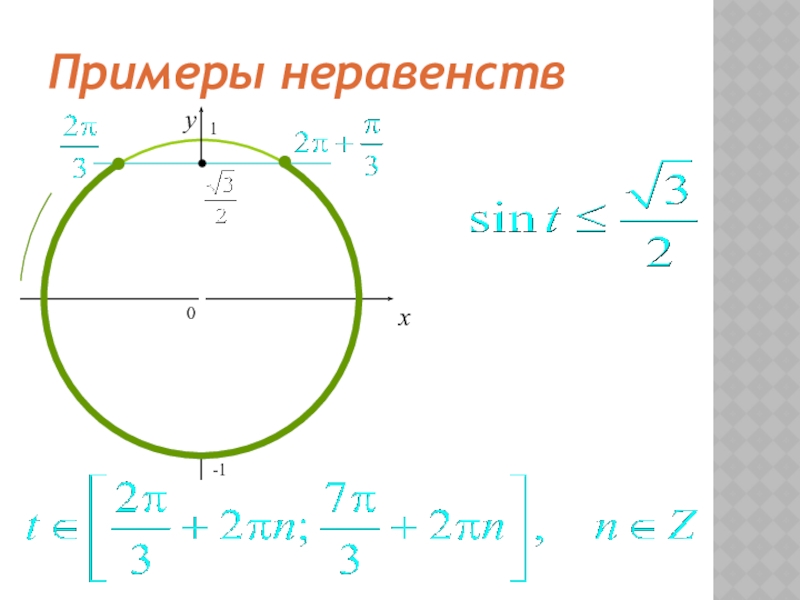
- 28. Примеры неравенств0xy-11
Слайд 2ТРИГОНОМЕТРИЯ
Тригонометрия-это часть геометрии, где с помощью тригонометрических функций связываются элементы треугольника.
Тригонометрия-это объект математического анализа, где тригонометрические уравнения изучаются методами алгебры.
Слайд 3ЭТАПЫ РАЗВИТИЯ ТРИГОНОМЕТРИИ
Тригонометрия в древности являлась вспомогательным разделом астрономии. Древнегреческие ученые
Древнеиндийские ученые заменили хорды синусами.
В VIII веке математики Востока превратили тригонометрию в самостоятельную математическую дисциплину. Ими были введены другие тригонометрические функции и составлены таблицы.
Окончательный вид тригонометрия приобрела в XVIII веке в трудах Л.Эйлера.
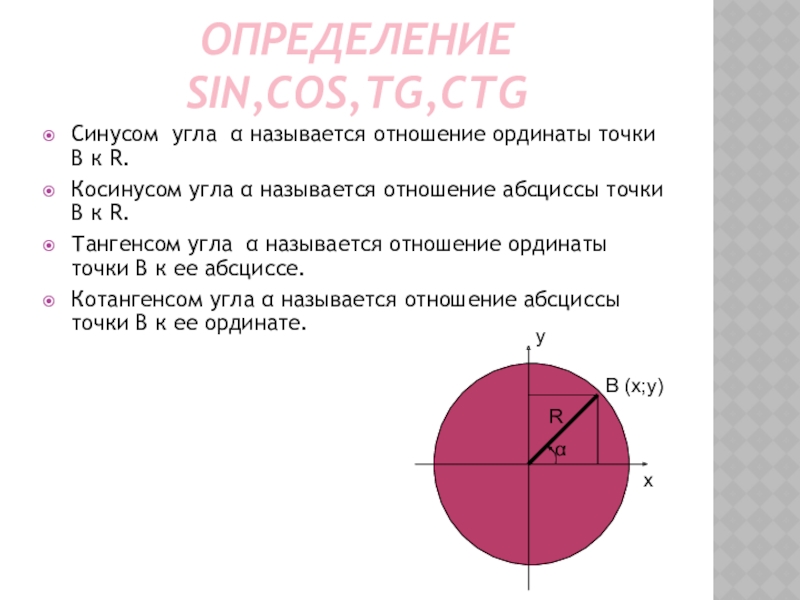
Слайд 4ОПРЕДЕЛЕНИЕ SIN,COS,TG,CTG
Синусом угла α называется отношение ординаты точки В к R.
Косинусом
Тангенсом угла α называется отношение ординаты точки В к ее абсциссе.
Котангенсом угла α называется отношение абсциссы точки В к ее ординате.
R
α
R
B (x;y)
y
x
Слайд 8ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА
sin² α + cos² α = 1
tg α
tg α = sin α ÷ cos α
ctg α = cos α ÷ sin α
1 + tg² α = 1 ÷ cos² α
1 + ctg² α = 1 ÷ sin² α
Слайд 10ФОРМУЛЫ СЛОЖЕНИЯ
sin (α + β) = sin α · cos β
sin (α - β) = sin α · cos β - sin β · cos α
cos (α + β) = cos α · cos β - sin α · sin β
cos (α - β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
Слайд 11ФОРМУЛЫ ДВОЙНОГО УГЛА
cos 2α = cos² α - sin² α
cos 2α
cos 2α = 1 - 2sin² α
sin 2α = 2sin α · cos α
tg 2α = (2tg α) ÷ (1 - tg² α)
ctg 2α = (ctg² α - 1) ÷ (2ctg α)
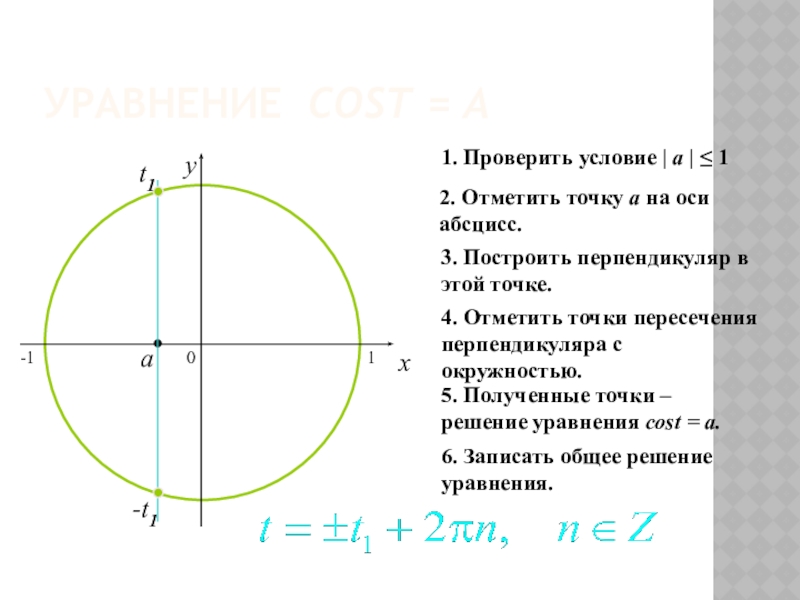
Слайд 15УРАВНЕНИЕ COST = A
0
x
y
2. Отметить точку а на оси абсцисс.
3. Построить
4. Отметить точки пересечения перпендикуляра с окружностью.
5. Полученные точки – решение уравнения cost = a.
6. Записать общее решение уравнения.
1. Проверить условие | a | ≤ 1
a
t1
-t1
-1
1
Слайд 16УРАВНЕНИЕ SINT = A
0
x
y
2. Отметить точку а на оси ординат.
3. Построить
4. Отметить точки пересечения перпендикуляра с окружностью.
5. Полученные точки – решение уравнения sint = a.
6. Записать общее решение уравнения.
1. Проверить условие | a | ≤ 1
a
t1
π-t1
-1
1
Слайд 23НЕРАВЕНСТВО COST > A
0
x
y
1. Отметить на оси абсцисс интервал x >
2. Выделить дугу окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
t1
-t1
-1
1
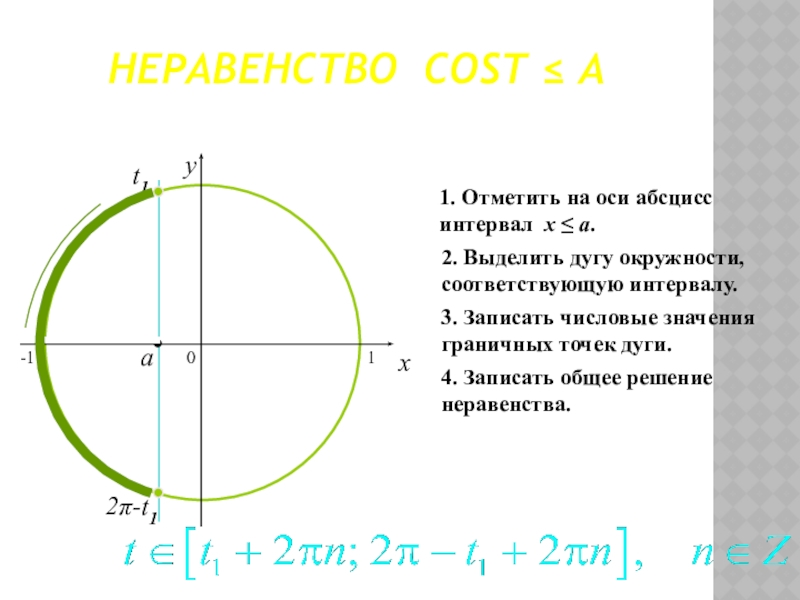
Слайд 24НЕРАВЕНСТВО COST ≤ A
0
x
y
1. Отметить на оси абсцисс интервал x ≤
2. Выделить дугу окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
t1
2π-t1
-1
1
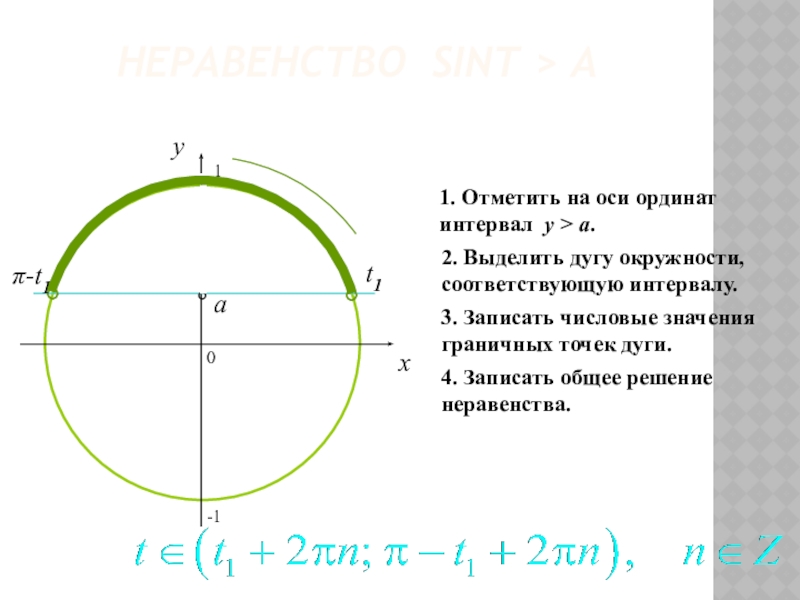
Слайд 25НЕРАВЕНСТВО SINT > A
0
x
y
1. Отметить на оси ординат интервал y >
2. Выделить дугу окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
t1
π-t1
-1
1
Слайд 26НЕРАВЕНСТВО SINT ≤ A
0
x
y
1. Отметить на оси ординат интервал y≤a.
2. Выделить
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
3π-t1
t1
-1
1