курсе «Уравнения и неравенства»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа на тему Уравнения с параметром в элективном курсе Уравнения и неравенства (10 - 11 класс)
Содержание
- 1. Презентация по алгебре и началам анализа на тему Уравнения с параметром в элективном курсе Уравнения и неравенства (10 - 11 класс)
- 2. Актуальность темыЗадачи с параметром встречаются волимпиадных заданияхвариантах
- 3. Грачев Василий Федорович, учитель высшей категории МОУ
- 4. Тематическое планированиеИррациональные преобразования выражений (5 ч)Рациональные выражения
- 5. Пояснительная запискаОдним их самых трудных материалов с
- 6. Цели методической разработкиЗнакомство учащихся с конкретными методами
- 7. Задачи методической разработкиПовышение математического и логического уровня
- 8. Технология деятельностного, исследовательского методов, алгоритмизации обучения. 1.
- 9. ТЕХНОЛОГИЯ ДЕЯТЕЛЬНОСТНОГО, ИССЛЕДОВАТЕЛЬСКОГО МЕТОДОВ, АЛГОРИТМИЗАЦИИ ОБУЧЕНИЯ. 2.
- 10. Технология деятельностного, исследовательского методов, алгоритмизации обучения. 3.
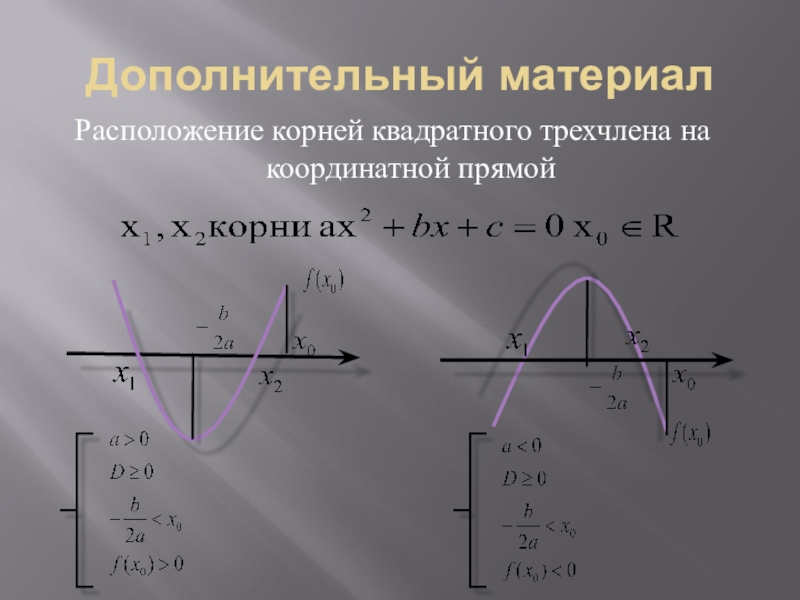
- 11. Дополнительный материалРасположение корней квадратного трехчлена на координатной прямой
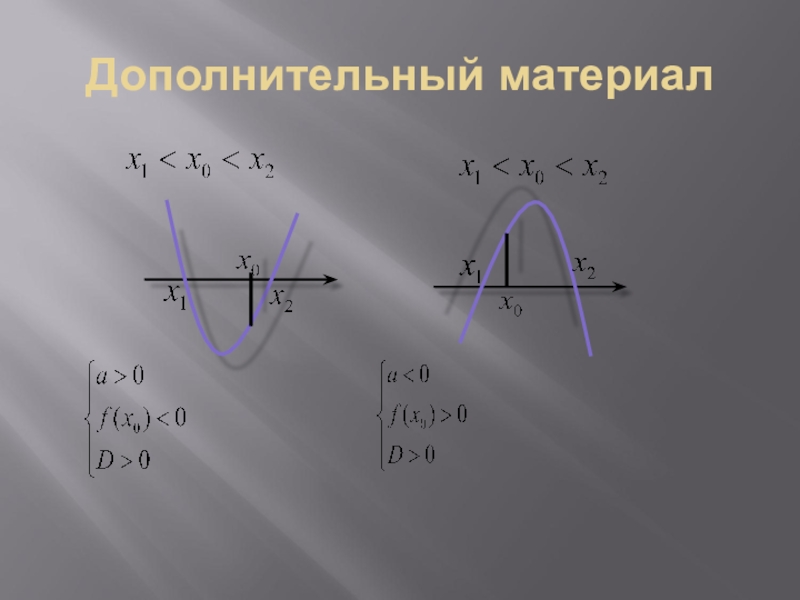
- 12. Дополнительный материал
- 13. Дополнительный материал
- 14. ПримерНайти все значения а, при которых неравенство
- 15. ПримерПри каких значениях параметра к уравнениеИмеет 4
- 16. Заданиенайдите все значения а, при каждом их
- 17. ЗаданиеНайдите все значения а, такие что для
- 18. Дополнительный материалПрименение знакопостоянства производной при решении уравнений с параметром
- 19. ПримерПри каких а, функция
- 20. Дополнительный материал
- 21. Пример
- 22. Дополнительный материалИспользование уравнения касательной при решении уравнений с параметром:
- 23. ПримерПри каких значениях а уравнение
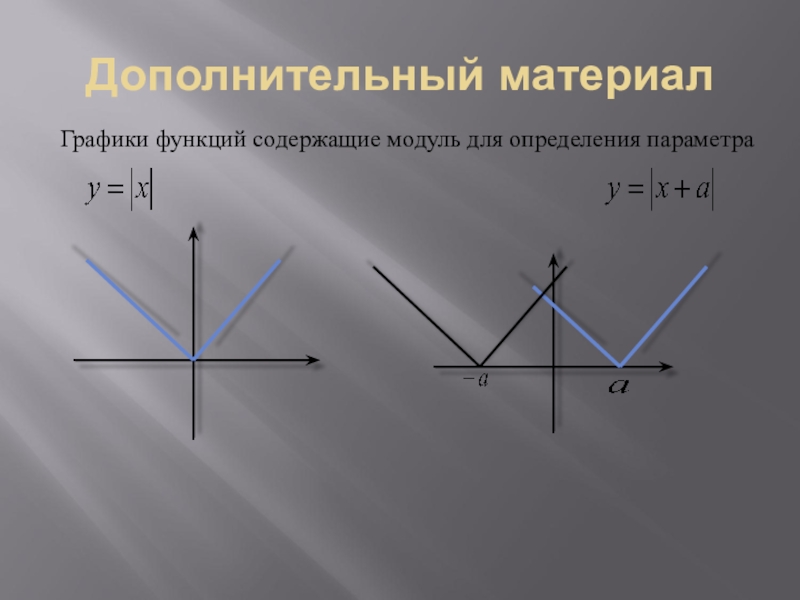
- 24. Дополнительный материалГрафики функций содержащие модуль для определения параметра
- 25. ПримерНайти все значения в, при каждом из
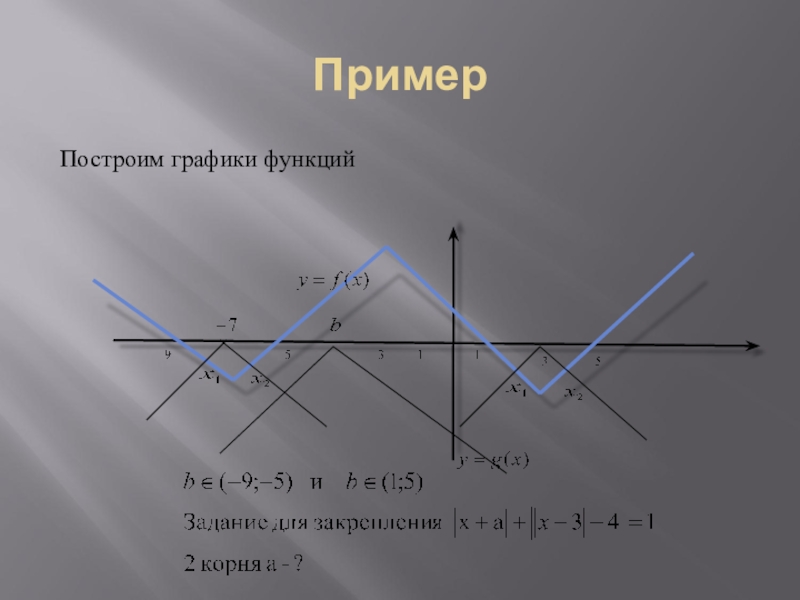
- 26. ПримерПостроим графики функций
- 27. ПримерГрафический способ решения уравнений с параметром1) При
- 28. Задание При каких значениях параметра а существует единственная
- 29. «Голова, наполненная отрывочными, бессвязными знаниями, похожа на
Актуальность темыЗадачи с параметром встречаются волимпиадных заданияхвариантах ЕГЭвступительных заданиях в вузПроблемыоднотипные задания в учебникахтрудности при изучении темыневысокое качество знаний
Слайд 2Актуальность темы
Задачи с параметром встречаются в
олимпиадных заданиях
вариантах ЕГЭ
вступительных заданиях в вуз
Проблемы
однотипные
задания в учебниках
трудности при изучении темы
невысокое качество знаний
трудности при изучении темы
невысокое качество знаний
Слайд 3Грачев Василий Федорович, учитель высшей категории МОУ СОШ №17
г. Саров
Образование:
Арзамасский государственный педагогический институт имени А.П.Гайдара (1983)
Специальность: Физика, Математика
Квалификация: учитель математики
Категория: Высшая 2005г.
Стаж работы в МОУ СОШ №17: 17 лет
Награды: 1. Почетная грамота администрации г. Саров
2. Почетная грамота департамента образования
г. Саров
3. Благодарственное письмо департамента образования
г. Саров
Специальность: Физика, Математика
Квалификация: учитель математики
Категория: Высшая 2005г.
Стаж работы в МОУ СОШ №17: 17 лет
Награды: 1. Почетная грамота администрации г. Саров
2. Почетная грамота департамента образования
г. Саров
3. Благодарственное письмо департамента образования
г. Саров
Краткая характеристика
Слайд 4Тематическое планирование
Иррациональные преобразования выражений (5 ч)
Рациональные выражения (6 ч)
Рациональные неравенства (6)
Зачетная
работа (2 ч)
Показательные уравнения (6 ч)
Показательные неравенства (6 ч)
Зачетная работа (2 ч)
Логарифмические уравнения (6 ч)
Логарифмические неравенства (6 ч)
Зачетная работа (2 ч)
Иррациональные уравнения (6 ч)
Иррациональные неравенства (6 ч)
Зачетная работа (2 ч)
Итоговое тестирование (2 ч)
Резерв (1 ч)
Показательные уравнения (6 ч)
Показательные неравенства (6 ч)
Зачетная работа (2 ч)
Логарифмические уравнения (6 ч)
Логарифмические неравенства (6 ч)
Зачетная работа (2 ч)
Иррациональные уравнения (6 ч)
Иррациональные неравенства (6 ч)
Зачетная работа (2 ч)
Итоговое тестирование (2 ч)
Резерв (1 ч)
Слайд 5Пояснительная записка
Одним их самых трудных материалов с которыми приходиться встречаться выпускникам
на ЕГЭ – это задания с параметром.
Научиться подбирать необходимые приемы решения примеров с параметрами позволяет данная методическая разработка.
Можно утверждать, что если выпускник сознательно усвоит приемы решения примеров, то его знание существенно улучшиться, а это, в свою очередь благотворно скажется на суммарной оценке по математике.
Научиться подбирать необходимые приемы решения примеров с параметрами позволяет данная методическая разработка.
Можно утверждать, что если выпускник сознательно усвоит приемы решения примеров, то его знание существенно улучшиться, а это, в свою очередь благотворно скажется на суммарной оценке по математике.
Слайд 6Цели методической разработки
Знакомство учащихся с конкретными методами решения уравнений с параметром
Подготовка
выпускников к заданию С-5 ЕГЭ
Освоение учащимися алгебры на повышенном уровне
Освоение учащимися алгебры на повышенном уровне
Слайд 7Задачи методической разработки
Повышение математического и логического уровня мышления учащихся
Развитие навыков исследовательской
деятельности
Подготовка к сдаче ЕГЭ по математике
Подготовка к сдаче ЕГЭ по математике
Слайд 8Технология деятельностного, исследовательского методов, алгоритмизации обучения.
1. Технология деятельстного метода
Основные принципы:
Принцип
деятельности
Принцип непрерывности
Принцип целостного представления о мире
Принцип психологической комфортности
Принцип творчества
Принцип вариативности
Принцип непрерывности
Принцип целостного представления о мире
Принцип психологической комфортности
Принцип творчества
Принцип вариативности
Слайд 9ТЕХНОЛОГИЯ ДЕЯТЕЛЬНОСТНОГО, ИССЛЕДОВАТЕЛЬСКОГО МЕТОДОВ, АЛГОРИТМИЗАЦИИ ОБУЧЕНИЯ.
2. Исследовательский метод
Основные этапы организации
учебно-исследовательской деятельности:
мотивация к проведению исследования;
постановка общей проблемы;
постановка задачи-исследования;
сбор информации: изучение учебной литературы, проведение эксперимента;
создание базы собранных данных;
выдвижение на ее основе гипотезы;
проверка гипотезы: доказательство или опровержение;
формулирование выводов;
демонстрация актуальности проведенного исследования и возможностей применения его результатов.
мотивация к проведению исследования;
постановка общей проблемы;
постановка задачи-исследования;
сбор информации: изучение учебной литературы, проведение эксперимента;
создание базы собранных данных;
выдвижение на ее основе гипотезы;
проверка гипотезы: доказательство или опровержение;
формулирование выводов;
демонстрация актуальности проведенного исследования и возможностей применения его результатов.
Слайд 10Технология деятельностного, исследовательского методов, алгоритмизации обучения.
3. Алгоритмизация в обучении
Свойства алгоритма:
детерминированность;
однозначность;
массовость;
дискретность;
понятность.
Основные этапы при формировании алгоритма.
I. Введение алгоритма.
1) Актуализация знаний учащихся.
2) Открытие алгоритма.
3) Формулировка алгоритма.
II. Усвоение.
III. Применение алгоритма.
однозначность;
массовость;
дискретность;
понятность.
Основные этапы при формировании алгоритма.
I. Введение алгоритма.
1) Актуализация знаний учащихся.
2) Открытие алгоритма.
3) Формулировка алгоритма.
II. Усвоение.
III. Применение алгоритма.
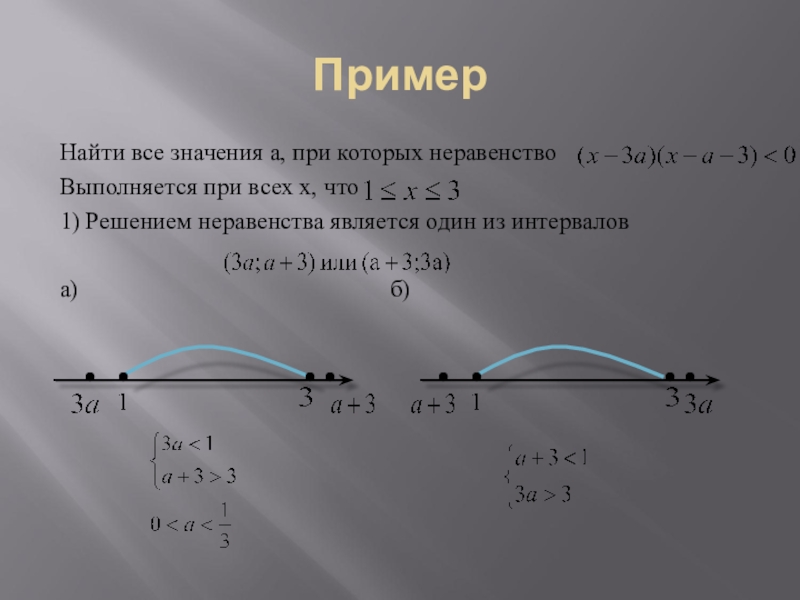
Слайд 14Пример
Найти все значения а, при которых неравенство
Выполняется при всех х,
что
1) Решением неравенства является один из интервалов
а) б)
1) Решением неравенства является один из интервалов
а) б)
Слайд 15Пример
При каких значениях параметра к уравнение
Имеет 4 корня:
1)
а)
б)
к=0 4 корня
1Задание для самостоятельного решения: к=? 2 корня
к=0 4 корня
1
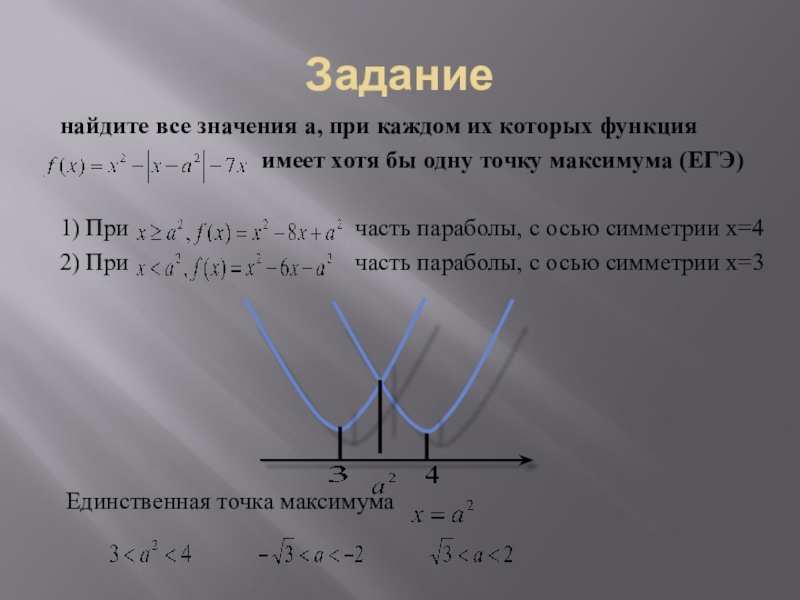
Слайд 16Задание
найдите все значения а, при каждом их которых функция
имеет хотя бы одну точку максимума (ЕГЭ)
1) При часть параболы, с осью симметрии х=4
2) При часть параболы, с осью симметрии х=3
Единственная точка максимума
1) При часть параболы, с осью симметрии х=4
2) При часть параболы, с осью симметрии х=3
Единственная точка максимума
Слайд 17Задание
Найдите все значения а, такие что для любого х, выполняется неравенство
1)
убывающая
2)
возрастающая
Наименьшее значение функции равно f(-a) или f(-1)
Слайд 18Дополнительный материал
Применение знакопостоянства производной при решении уравнений с параметром
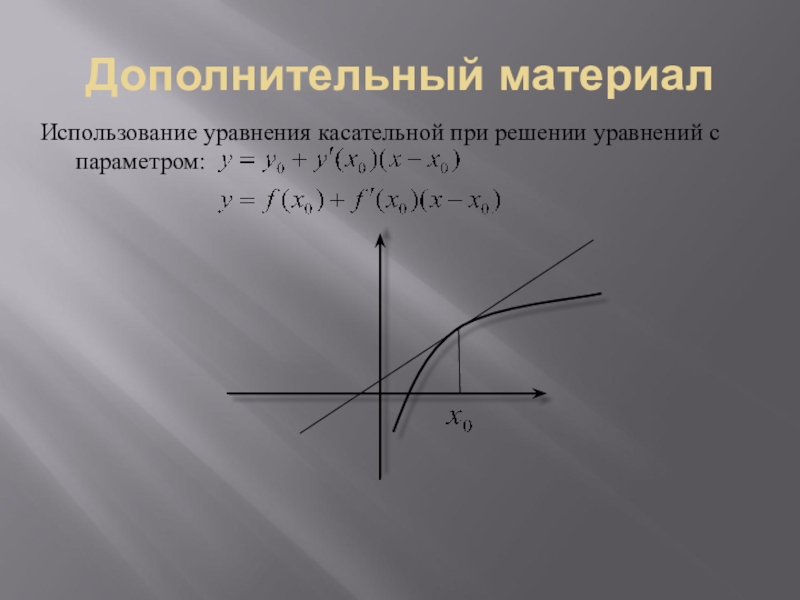
Слайд 22Дополнительный материал
Использование уравнения касательной при решении уравнений с параметром:
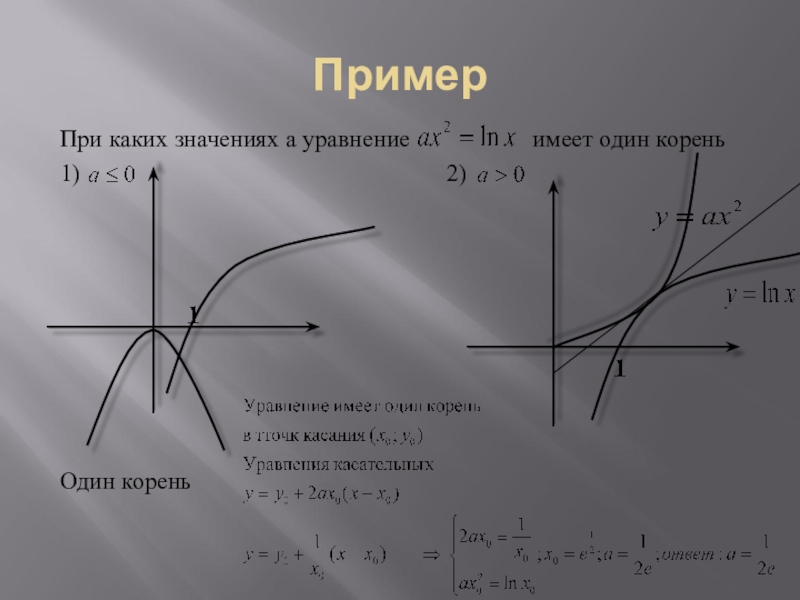
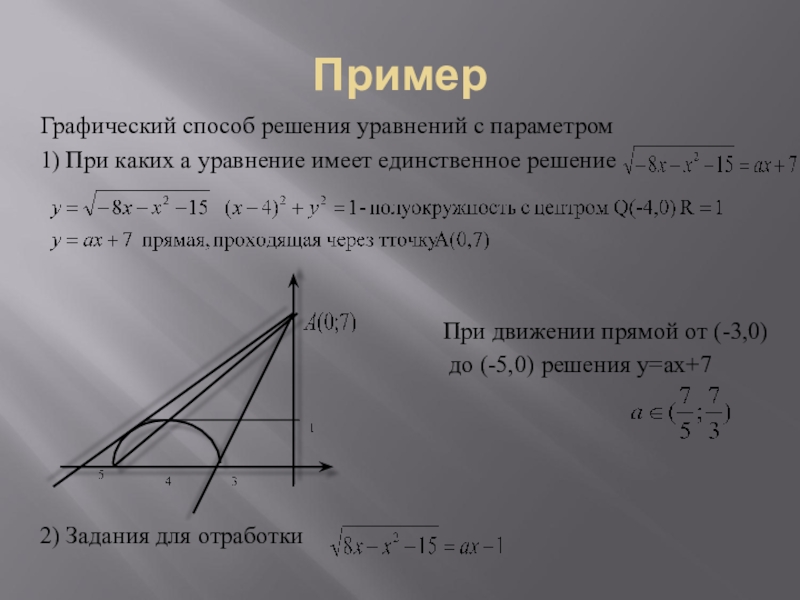
Слайд 27Пример
Графический способ решения уравнений с параметром
1) При каких а уравнение имеет
единственное решение
При движении прямой от (-3,0)
до (-5,0) решения у=ах+7
2) Задания для отработки
При движении прямой от (-3,0)
до (-5,0) решения у=ах+7
2) Задания для отработки
Слайд 28Задание
При каких значениях параметра а существует единственная пара чисел (х,у), удовлетворяющих
уравнению
Запишем уравнение относительно у:
Так как решение единственное, то D=0
Ответ: при а=0, а=2, х=3, у=-1
Замечание: при а=0
система имеет бесконечное множество решений
Запишем уравнение относительно у:
Так как решение единственное, то D=0
Ответ: при а=0, а=2, х=3, у=-1
Замечание: при а=0
система имеет бесконечное множество решений
1)
2)
Слайд 29«Голова, наполненная отрывочными, бессвязными знаниями, похожа на кладовую, в которой все
в беспорядке и где сам хозяин ничего не отыщет; голова, где только система без знаний, похожа на лавку, в которой на всех ящиках есть надписи, а в ящиках пусто. Истинная педагогика, избегая обеих крайностей, дает ученикам прежде материал и по мере накопления этого материала приводит его в систему. Чем больше и разнообразнее накопляется материал, тем выше становится система и, наконец, достигает до отвлеченности логических и философских положений».
К.Д. Ушинский.
Спасибо за внимание!
К.Д. Ушинский.
Спасибо за внимание!