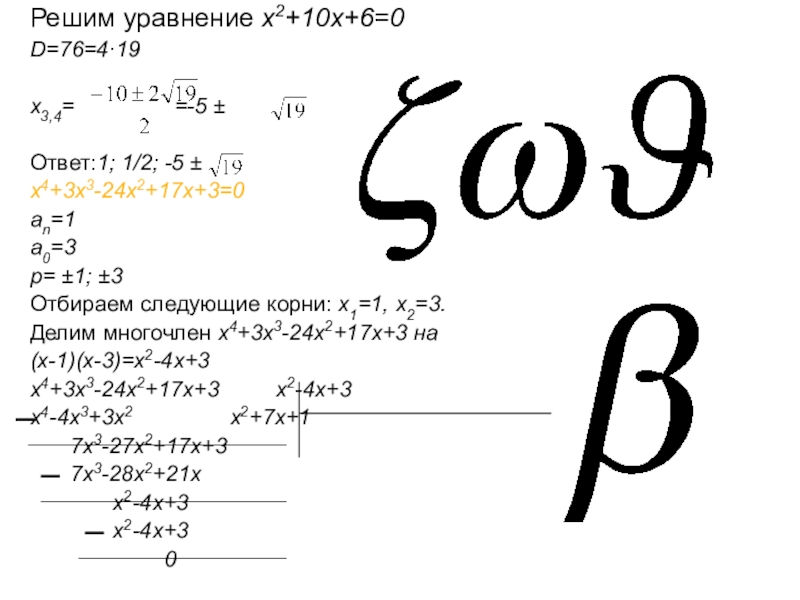Подготовила учитель
высшей категории МБОУ гимназии № 42
Тронина Л.Ю.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа по теме Решение уравнений (11 класс)
Содержание
- 1. Презентация по алгебре и началам анализа по теме Решение уравнений (11 класс)
- 2. Готовимся к ЕГЭ
- 3. Решение уравненийЦели урока. Повторить и закрепить ранее
- 4. Задание по группам1 группа2 группа3 группа4 группа
- 5. Проверка 1 группаа)610x-1=36 610x-1=6210x-1=2x=0,3x Є (0;1) (3)б)log x2=log (9x-20)x2=9x-20x2-9x+20=0x1=4; x2=5x1+x2=9 (4)
- 6. 2 группа а) 4x-2=(1/2)1-x
- 7. 3 группаа) 3x+2+3x+1+3x=39 3x·32+3x·3+3x=39
- 8. 4 группаа) 49·72x-50·7x+1=0 7x=t, t>0
- 9. Слайд 9
- 10. Решая уравнения 3,4 и более высоких степеней,
- 11. II. Отыскание рациональных корней уравнений с целыми
- 12. 2x4+17x3-17x2-8x+6=0a0=6p= ±1, ±2, ±3, ±6an=2q=1;2p/q= ±1, ±2,
- 13. Решим уравнение x2+10x+6=0D=76=4·19x3,4= =-5 ±Ответ:1; 1/2;
- 14. Решаем уравнение x2+7x+1=0D=45, x3,4=Ответ:1;3; Надо отметить следующее, что
- 15. Рассмотрим уравнение тестового задания ЕГЭ из части
- 16. Подставляем эти числа в уравнение, отбираем следующие
- 17. IV. Задание на дом2x4-5x3-x2+3x+1=0;X4+2x3-11x2+4x+4=0;X4+3x3-4x2+x+1=0;logx(x -9x+92·3x-1-101+2·33-x)=1,2
Готовимся к ЕГЭ
Слайд 1Открытый урок по алгебре и началам анализа в 11 классе физико-математического
профиля по теме «Решение уравнений (в рамках подготовки к экзамену)».
Слайд 3Решение уравнений
Цели урока. Повторить и закрепить ранее изученный материал (показательные и
логарифмические уравнения).
Познакомить учащихся с решением уравнений высших степеней, используя деление многочлена на многочлен.
Вырабатывать навыки решения уравнений высших степеней.
Воспитывать культуру математической речи.
Познакомить учащихся с решением уравнений высших степеней, используя деление многочлена на многочлен.
Вырабатывать навыки решения уравнений высших степеней.
Воспитывать культуру математической речи.
Ход урока
I.Повторение
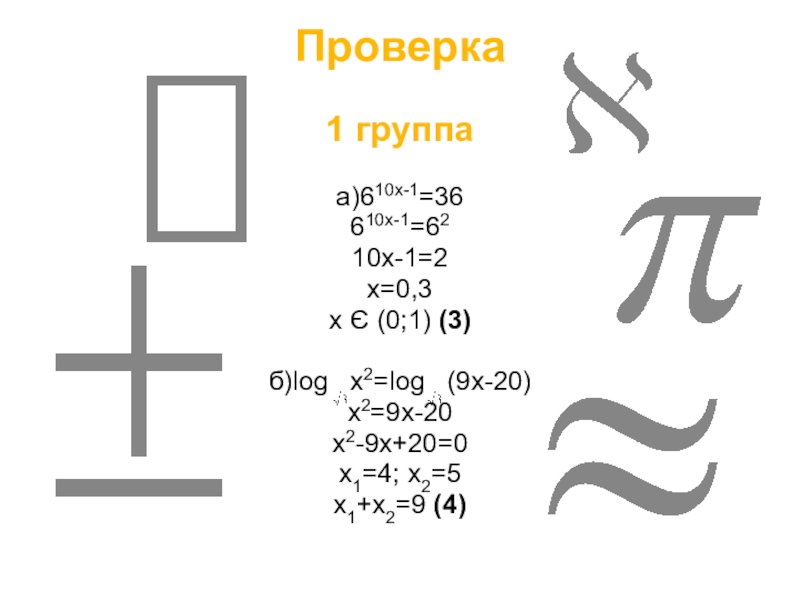
Слайд 5Проверка
1 группа
а)610x-1=36
610x-1=62
10x-1=2
x=0,3
x Є (0;1) (3)
б)log x2=log (9x-20)
x2=9x-20
x2-9x+20=0
x1=4; x2=5
x1+x2=9
(4)
Слайд 6
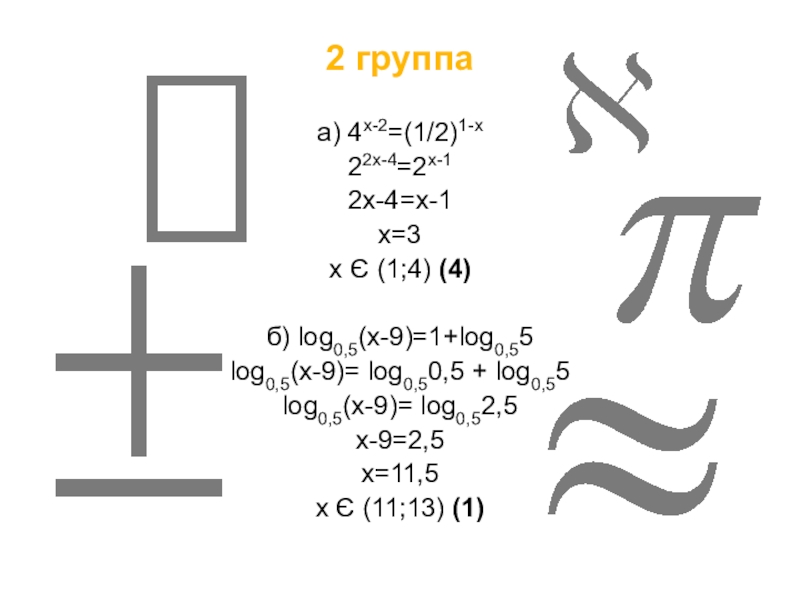
2 группа
а) 4x-2=(1/2)1-x
22x-4=2x-1
2x-4=x-1
x=3
x Є (1;4) (4)
б) log0,5(x-9)=1+log0,55
log0,5(x-9)= log0,50,5 + log0,55
log0,5(x-9)= log0,52,5
x-9=2,5
x=11,5
x Є (11;13) (1)
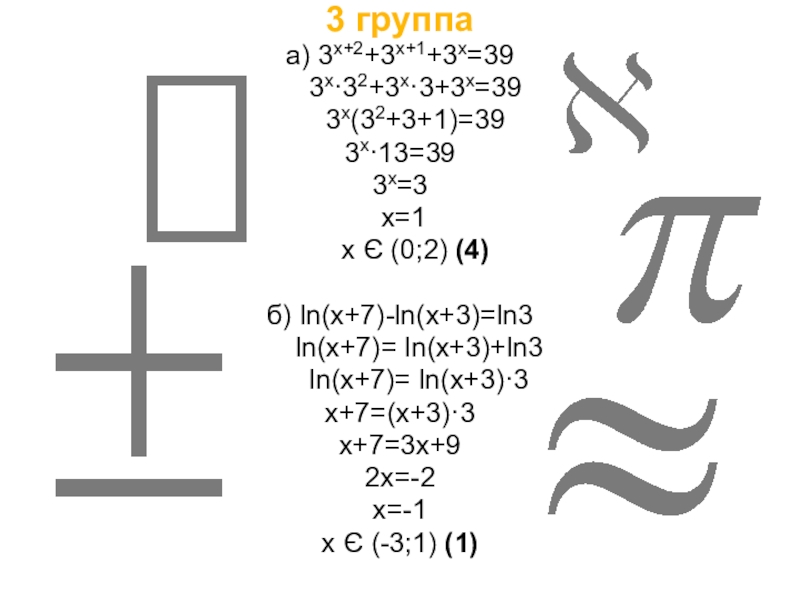
Слайд 73 группа
а) 3x+2+3x+1+3x=39
3x·32+3x·3+3x=39
3x(32+3+1)=39
3x·13=39
3x=3
x=1
x Є (0;2) (4)
б) ln(x+7)-ln(x+3)=ln3
ln(x+7)= ln(x+3)+ln3
ln(x+7)= ln(x+3)·3
x+7=(x+3)·3
x+7=3x+9
2x=-2
x=-1
x Є (-3;1) (1)
Слайд 8
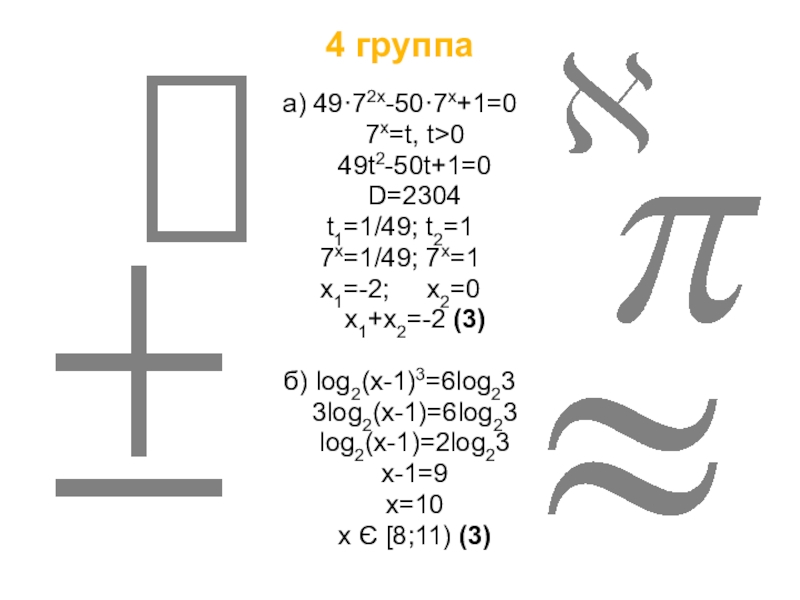
4 группа
а) 49·72x-50·7x+1=0
7x=t, t>0
49t2-50t+1=0
D=2304
t1=1/49; t2=1
7x=1/49;
7x=1
x1=-2; x2=0
x1+x2=-2 (3)
б) log2(x-1)3=6log23
3log2(x-1)=6log23
log2(x-1)=2log23
x-1=9
x=10
x Є [8;11) (3)
x1=-2; x2=0
x1+x2=-2 (3)
б) log2(x-1)3=6log23
3log2(x-1)=6log23
log2(x-1)=2log23
x-1=9
x=10
x Є [8;11) (3)
Слайд 9
X3-3x2-3x+1=0
(x3+1)-(3x2+3x)=0
(x+1)(x2-x+1)-3x(x+1)=0
(x+1)(x2-x+1-3x)=0
(x+1)(x2-4x+1)=0
x+1=0 или x2-4x+1=0
x1=-1
D=12
x2,3=2±
Ответ: -1; 2±
x2,3=2±
Ответ: -1; 2±
Все уравнения, которые были решены, являются достаточно простыми. Для того, чтобы успешно справиться с тестовыми заданиями второй части экзамена, нужно уметь решать уравнения более сложные, в которых переменная содержится в степени, большей 2.
Например,
Слайд 10 Решая уравнения 3,4 и более высоких степеней, мы стремимся многочлены, которые
в них встречаются, разложить на множители. В данном примере это удалось, мы воспользовались ранее известными нам способами разложения на множители. Как быть в том случае, когда нельзя вынести общий множители за скобки, сгруппировать слагаемые или применить формулы сокращенного умножения?
Сегодня мы знакомимся с темой:
Сегодня мы знакомимся с темой:
Слайд 11II. Отыскание рациональных корней уравнений с целыми коэффициентами
Уравнение anxn+an-1xn-1+…+a0=c,
имеющее рациональные коэффициенты, равносильно уравнению того же вида, имеющему целые коэффициенты.
Например, 3/5x3-2/3x2-1/6=0 равносильно уравнению 18x3-20x2-5=0
Для того, чтобы несократимая дробь p/q была корнем уравнения anxn+an-1xn-1+…+a0=0 (1), необходимо, чтобы числитель p этой дроби был делителем свободного члена a0, а знаменатель q – делителем коэффициента an при старшем члене.
Таким образом, чтобы найти рациональные корни p/q уравнения (1), надо:
найти все целые делители свободного члена (положительные и отрицательные);
найти все натуральные делители коэффициента an при старшем члене;
составить дроби с найденными возможными значениями числителя и знаменателя;
из найденных дробей отобрать те, которые удовлетворяют заданному уравнению.
Если уравнение (1) приведенное, т.е. an=1, то все рациональные корни уравнения являются целыми числами – делителями свободного члена a0.
Например, 3/5x3-2/3x2-1/6=0 равносильно уравнению 18x3-20x2-5=0
Для того, чтобы несократимая дробь p/q была корнем уравнения anxn+an-1xn-1+…+a0=0 (1), необходимо, чтобы числитель p этой дроби был делителем свободного члена a0, а знаменатель q – делителем коэффициента an при старшем члене.
Таким образом, чтобы найти рациональные корни p/q уравнения (1), надо:
найти все целые делители свободного члена (положительные и отрицательные);
найти все натуральные делители коэффициента an при старшем члене;
составить дроби с найденными возможными значениями числителя и знаменателя;
из найденных дробей отобрать те, которые удовлетворяют заданному уравнению.
Если уравнение (1) приведенное, т.е. an=1, то все рациональные корни уравнения являются целыми числами – делителями свободного члена a0.
Слайд 122x4+17x3-17x2-8x+6=0
a0=6
p= ±1, ±2, ±3, ±6
an=2
q=1;2
p/q= ±1, ±2, ±3, ±6; ±1/2; ±3/2
x1=1;
x2=1/2.
Многочлен 2x4+17x3-17x2-8x+6 делится на
2(x-1)(x-1/2)=2x2-3x+1.
2x4+17x3-17x2-8x+6 2x2-3x+1
2x4-3x3+x2 x2+10x+6
20x3-18x2-8x+6
20x3-30x2+10x
12x2-18x+6
12x2-18x+6
0
2(x-1)(x-1/2)( x2+10x+6)=0
Многочлен 2x4+17x3-17x2-8x+6 делится на
2(x-1)(x-1/2)=2x2-3x+1.
2x4+17x3-17x2-8x+6 2x2-3x+1
2x4-3x3+x2 x2+10x+6
20x3-18x2-8x+6
20x3-30x2+10x
12x2-18x+6
12x2-18x+6
0
2(x-1)(x-1/2)( x2+10x+6)=0
Слайд 13Решим уравнение x2+10x+6=0
D=76=4·19
x3,4= =-5 ±
Ответ:1; 1/2; -5 ±
x4+3x3-24x2+17x+3=0
an=1
a0=3
p= ±1; ±3
Отбираем
следующие корни: x1=1, x2=3.
Делим многочлен x4+3x3-24x2+17x+3 на
(x-1)(x-3)=x2-4x+3
x4+3x3-24x2+17x+3 x2-4x+3
x4-4x3+3x2 x2+7x+1
7x3-27x2+17x+3
7x3-28x2+21x
x2-4x+3
x2-4x+3
0
Делим многочлен x4+3x3-24x2+17x+3 на
(x-1)(x-3)=x2-4x+3
x4+3x3-24x2+17x+3 x2-4x+3
x4-4x3+3x2 x2+7x+1
7x3-27x2+17x+3
7x3-28x2+21x
x2-4x+3
x2-4x+3
0
Слайд 14Решаем уравнение x2+7x+1=0
D=45, x3,4=
Ответ:1;3;
Надо отметить следующее, что любой целый корень уравнения
с целыми коэффициентами является делителем его свободного члена.
III. Решить самостоятельно:
гр. 2x3-7x2+5x-1=0
гр. 8x3-4x+1=0
гр. 2x4-5x3+5x2-2=0
гр. 2x3-3x2-4x-1=0
III. Решить самостоятельно:
гр. 2x3-7x2+5x-1=0
гр. 8x3-4x+1=0
гр. 2x4-5x3+5x2-2=0
гр. 2x3-3x2-4x-1=0
Слайд 15Рассмотрим уравнение тестового задания ЕГЭ из части С, для решения которого
нужно будет воспользоваться выше указанным способом.
logx(x +2x+2+25·21-x-27-3·0,25x-1,5)=4/3
Так как x-основание логарифма, то x >0 и x≠1.
logx(x +2x+2+25·21-x-27-3·(2-2)x-1,5)=logxx4/3
X4/3+4·2x+50·1/2x -27-24·1/22x=x4/3
4·2x+50·1/2x -27-24·1/22x=0 ·22x
4·23x-27· 22x +50· 2x -24=0
2x=t, t>0
4t3-27t2+50t-24=0
a0=-24
p= ±1; ±2; ±3; ±4; ±6; ±8; ±12; ±24;
an=4
q=1;2;4
p/q=±1; ±2; ±3; ±4; ±6; ±8; ±12; ±24; ±1/2; ±3/2; ±3/4
logx(x +2x+2+25·21-x-27-3·0,25x-1,5)=4/3
Так как x-основание логарифма, то x >0 и x≠1.
logx(x +2x+2+25·21-x-27-3·(2-2)x-1,5)=logxx4/3
X4/3+4·2x+50·1/2x -27-24·1/22x=x4/3
4·2x+50·1/2x -27-24·1/22x=0 ·22x
4·23x-27· 22x +50· 2x -24=0
2x=t, t>0
4t3-27t2+50t-24=0
a0=-24
p= ±1; ±2; ±3; ±4; ±6; ±8; ±12; ±24;
an=4
q=1;2;4
p/q=±1; ±2; ±3; ±4; ±6; ±8; ±12; ±24; ±1/2; ±3/2; ±3/4
Слайд 16Подставляем эти числа в уравнение, отбираем следующие корни: t1=2, t2=3/4.
Разделим многочлен
4t3-27t2+50t-24 на
4(t-2)(t-3/4)=4t2-11t+6
4t3-27t2+50t-24 4t2-11t+6
4t3-11t2+6t t-4
-16t2+44t-24
-16t2+44t-24
0
Решаем уравнение t-4=0
t3=4
Таким образом, 2x=2; 2x=3/4; 2x=4
Из первого уравнения x1=1 О.Д.З.
Из второго уравнения x2=log23/4
x2=log23-log24<0
Из третьего уравнения x3=2
Ответ:2
4(t-2)(t-3/4)=4t2-11t+6
4t3-27t2+50t-24 4t2-11t+6
4t3-11t2+6t t-4
-16t2+44t-24
-16t2+44t-24
0
Решаем уравнение t-4=0
t3=4
Таким образом, 2x=2; 2x=3/4; 2x=4
Из первого уравнения x1=1 О.Д.З.
Из второго уравнения x2=log23/4
x2=log23-log24<0
Из третьего уравнения x3=2
Ответ:2