«Лицей №51 имени Капустина Бориса Владиславовича»
Овчар Людмила Леонидовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа 11 класс на тему Решение систем уравнений
Содержание
- 1. Презентация по алгебре и началам анализа 11 класс на тему Решение систем уравнений
- 2. Исторические сведенияУравнение с двумя неизвестными, входящее в
- 3. Исторические сведенияИздавна применялись приемы исключения неизвестных из
- 4. Исторические сведения
- 5. Исторические сведения
- 6. Способы решения систем уравнений Графический – оба
- 7. Способы решения систем уравнений (аналитические методы)
- 8. Способы решения систем уравнений (аналитические методы)
- 9. Способы решения систем уравнений (аналитические методы)
- 10. Способы решения систем уравнений (аналитические методы)
- 11. ответы
- 12. Система maximaMaxima - программа для выполнения математических
- 13. Система maxima для решения систем уравненийДля решения
- 14. Результат решенной системы в программе maxima№1
- 15. Результат решенной системы в программе maxima№6
- 16. Возможности применения системы maxima при решении систем
- 17. Спасибо за внимание!
Исторические сведенияУравнение с двумя неизвестными, входящее в систему, выражает зависимость между двумя величинами , имеет бесчисленное множество решений и является неопределенным.Решением таких уравнений занимались в древности китайцы, греки, вавилоняне и индийцы.В «Арифметике» Диофанта приведено много задач,
Слайд 1Решение систем рациональных уравнений
Автор: учитель математики высшей категории МБОУ города Ростова-на-Дону
Слайд 2Исторические сведения
Уравнение с двумя неизвестными, входящее в систему, выражает зависимость между
двумя величинами , имеет бесчисленное множество решений и является неопределенным.
Решением таких уравнений занимались в древности китайцы, греки, вавилоняне и индийцы.
В «Арифметике» Диофанта приведено много задач, решаемых им с помощью неопределенных уравнений.
Дата рождения и смерти не установлены
Место рождения: Александрия, Египет
Страна: Древний Рим
Научная сфера: Теория чисел
Известен, как «отец алгебры»
Решением таких уравнений занимались в древности китайцы, греки, вавилоняне и индийцы.
В «Арифметике» Диофанта приведено много задач, решаемых им с помощью неопределенных уравнений.
Дата рождения и смерти не установлены
Место рождения: Александрия, Египет
Страна: Древний Рим
Научная сфера: Теория чисел
Известен, как «отец алгебры»
Диофант
≈200-300 гг. нашей эры
Слайд 3Исторические сведения
Издавна применялись приемы исключения неизвестных из линейных уравнений. В ⅩⅤⅠⅠ
-ⅩⅤⅠⅠⅠ вв. их разрабатывали Ферма, Ньютон, Лейбниц, Эйлер, Безу, Лагранж…
Благодаря Ферма и Декарту, создавшим метод координат, стало возможным геометрическое решение уравнений системы.
Благодаря Ферма и Декарту, создавшим метод координат, стало возможным геометрическое решение уравнений системы.
Этьен Безу
(1730-1783)
Жозеф Луи Лагранж
(1736-1813)
Слайд 6Способы решения систем уравнений
Графический – оба графика уравнений строят в
одной системе координат, решением системы являются координаты точек пересечения графиков.(удобен при уравнениях, выражающих явно функции)
Подстановки – из одного уравнения выражают одну из переменных (обычно первую степень) и подставляют во второе уравнение; находят одну переменную, затем вторую.
Сложения – уравниваем при одной из переменной коэффициенты и складываем уравнения, исключая одну из переменных. Затем находим одну и вторую переменную.
Подстановки – из одного уравнения выражают одну из переменных (обычно первую степень) и подставляют во второе уравнение; находят одну переменную, затем вторую.
Сложения – уравниваем при одной из переменной коэффициенты и складываем уравнения, исключая одну из переменных. Затем находим одну и вторую переменную.
Слайд 12Система maxima
Maxima - программа для выполнения математических вычислений, символьных преобразований и
построения графиков. С каждой новой версией в Maxima появляются новые функциональные возможности и виды решаемых задач.
Целая и дробная часть десятичных дробей разделяются символом точка. Перед отрицательными числами ставится знак минус. Числитель и знаменатель обыкновенных дробей разделяется при помощи символа / (прямой слэш).
Арифметические операции
Обозначение арифметических операций в Maxima ничем не отличается от классического представления: + , - , * , /. Возведение в степень можно обозначать несколькими способами: ^ , ^^ , **. Извлечение корня степени n записываем, как степень 1/n. Введем еще одну полезную операцию - нахождение факториала числа. Эта операция обозначается восклицательным знаком, например 5!.
Для увеличения приоритета операции, как и в математике, используются круглые скобки: ().
Целая и дробная часть десятичных дробей разделяются символом точка. Перед отрицательными числами ставится знак минус. Числитель и знаменатель обыкновенных дробей разделяется при помощи символа / (прямой слэш).
Арифметические операции
Обозначение арифметических операций в Maxima ничем не отличается от классического представления: + , - , * , /. Возведение в степень можно обозначать несколькими способами: ^ , ^^ , **. Извлечение корня степени n записываем, как степень 1/n. Введем еще одну полезную операцию - нахождение факториала числа. Эта операция обозначается восклицательным знаком, например 5!.
Для увеличения приоритета операции, как и в математике, используются круглые скобки: ().
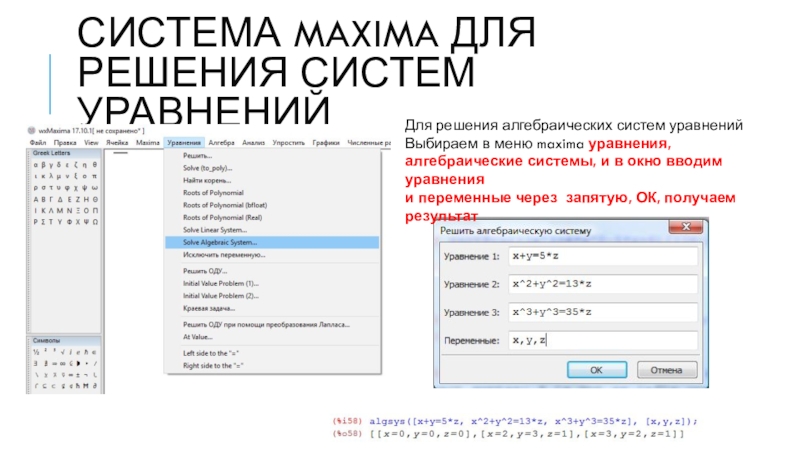
Слайд 13Система maxima для решения систем уравнений
Для решения алгебраических систем уравнений
Выбираем в
меню maxima уравнения,
алгебраические системы, и в окно вводим уравнения
и переменные через запятую, ОК, получаем результат
алгебраические системы, и в окно вводим уравнения
и переменные через запятую, ОК, получаем результат
Слайд 14Результат решенной системы в программе maxima
№1
algsys([2*x^2-x*y+3*y^2-7*x-12*y+1, x-y+1], [x,y]);
[[x=4,y=5],[x=-1/2,y=1/2]]
№2 algsys([x*y-x+y-7, x*y+x-y-13], [x,y]);
[[x=5,y=2],[x=-2,y=-5]]
№3 algsys([x^2-4*y^2-x*y+5-1, x^2+3*y^2-x*y-4*y+1], [x,y]);
[[x=1,y=1],[x=-(sqrt(631)*%i+3)/14,y=-3/7],[x=(sqrt(631)*%i-3)/14,y=-3/7],[x=0,y=1]] находятся в том числе и комплексные корни
№4 algsys([x^2+2*x*y-8*y^2-6*x+18*y-7, 2*x^2-5*x*y-10*y^2-3*x+9*y+7], [x,y]);
[[x=-1,y=2],[x=3,y=1],[x=1,y=1],[x=-3,y=-1]]
№5 algsys([x^3+4*y-y^3-16*x, 1+y^2-5*(1+x^2)], [x,y]);
[[x=-(8*%i)/sqrt(31),y=-(14*%i)/sqrt(31)],[x=(8*%i)/sqrt(31),y=(14*%i)/sqrt(31)],[x=-1,y=3],[x=1,y=-3],[x=0,y=2],[x=0,y=-2]]
[[x=4,y=5],[x=-1/2,y=1/2]]
№2 algsys([x*y-x+y-7, x*y+x-y-13], [x,y]);
[[x=5,y=2],[x=-2,y=-5]]
№3 algsys([x^2-4*y^2-x*y+5-1, x^2+3*y^2-x*y-4*y+1], [x,y]);
[[x=1,y=1],[x=-(sqrt(631)*%i+3)/14,y=-3/7],[x=(sqrt(631)*%i-3)/14,y=-3/7],[x=0,y=1]] находятся в том числе и комплексные корни
№4 algsys([x^2+2*x*y-8*y^2-6*x+18*y-7, 2*x^2-5*x*y-10*y^2-3*x+9*y+7], [x,y]);
[[x=-1,y=2],[x=3,y=1],[x=1,y=1],[x=-3,y=-1]]
№5 algsys([x^3+4*y-y^3-16*x, 1+y^2-5*(1+x^2)], [x,y]);
[[x=-(8*%i)/sqrt(31),y=-(14*%i)/sqrt(31)],[x=(8*%i)/sqrt(31),y=(14*%i)/sqrt(31)],[x=-1,y=3],[x=1,y=-3],[x=0,y=2],[x=0,y=-2]]
Слайд 15Результат решенной системы в программе maxima
№6 algsys([y^3+z^3-7*x^3, y-z-3*x, z-x-y+2], [x,y,z]);
[[x=1/2,y=1,z=-1/2],[x=1/2,y=(sqrt(111)*%i+5)/8,z=(sqrt(111)*%i-7)/8],[x=1/2,y=-(sqrt(111)*%i-5)/8,z=-(sqrt(111)*%i+7)/8]]
№7
algsys([x^2+3*x*y+y^2-61, x*y-12], [x,y]);
[[x=-3,y=-4],[x=-4,y=-3],[x=4,y=3],[x=3,y=4]]
№8 algsys([x^3+y^3-6, x*y-2], [x,y]);
[[x=1.259921095381759,y=1.587400917813934],[x=-1.091123635971722*%i-0.6299605249474369,y=1.374729636998602*%i-0.7937005259840997],[x=1.091123635971722*%i-0.6299605249474369,y=-1.374729636998602*%i-0.7937005259840997],[x=1.587400917813934,y=1.259921095381759],[x=-1.374729636998603*%i-0.7937005259840998,y=1.091123635971721*%i-0.6299605249474366],[x=1.374729636998603*%i-0.7937005259840998,y=-1.091123635971721*%i-0.6299605249474366]]
[[x=-3,y=-4],[x=-4,y=-3],[x=4,y=3],[x=3,y=4]]
№8 algsys([x^3+y^3-6, x*y-2], [x,y]);
[[x=1.259921095381759,y=1.587400917813934],[x=-1.091123635971722*%i-0.6299605249474369,y=1.374729636998602*%i-0.7937005259840997],[x=1.091123635971722*%i-0.6299605249474369,y=-1.374729636998602*%i-0.7937005259840997],[x=1.587400917813934,y=1.259921095381759],[x=-1.374729636998603*%i-0.7937005259840998,y=1.091123635971721*%i-0.6299605249474366],[x=1.374729636998603*%i-0.7937005259840998,y=-1.091123635971721*%i-0.6299605249474366]]
Слайд 16Возможности применения системы maxima при решении систем уравнений
maxima для школьников является
незаменимым помощником в изучении математики, физики, информатики, освобождая учащихся от рутинных расчетов и сосредотачивая их внимание на сущности метода решения той или иной задачи. Применение maxima позволяет решать целый спектр новых трудоемких, но интересных задач: от упрощения громоздких алгебраических выражений, аналитического решения уравнений и систем с параметрами, графических построений до анимации графиков и пошаговой визуализации самого процесса решения. Учащимся предоставляется возможность выполнять более содержательные задания и получать наглядные результаты. Это способствует закреплению знаний и умений, приобретенных ими при изучении других школьных дисциплин, помогает в полной мере проявлять свои творческие и исследовательские способности.












![Презентация по алгебре и началам анализа 11 класс на тему Решение систем уравнений Результат решенной системы в программе maxima№1 algsys([2*x^2-x*y+3*y^2-7*x-12*y+1, x-y+1], [x,y]); Результат решенной системы в программе maxima№1 algsys([2*x^2-x*y+3*y^2-7*x-12*y+1, x-y+1], [x,y]);](/img/tmb/7/687325/d51225673c7ae5483697adb1031cad4a-800x.jpg)
![Презентация по алгебре и началам анализа 11 класс на тему Решение систем уравнений Результат решенной системы в программе maxima№6 algsys([y^3+z^3-7*x^3, y-z-3*x, z-x-y+2], [x,y,z]);[[x=1/2,y=1,z=-1/2],[x=1/2,y=(sqrt(111)*%i+5)/8,z=(sqrt(111)*%i-7)/8],[x=1/2,y=-(sqrt(111)*%i-5)/8,z=-(sqrt(111)*%i+7)/8]]№7 algsys([x^2+3*x*y+y^2-61, x*y-12], [x,y]);[[x=-3,y=-4],[x=-4,y=-3],[x=4,y=3],[x=3,y=4]]№8 algsys([x^3+y^3-6, x*y-2], [x,y]);[[x=1.259921095381759,y=1.587400917813934],[x=-1.091123635971722*%i-0.6299605249474369,y=1.374729636998602*%i-0.7937005259840997],[x=1.091123635971722*%i-0.6299605249474369,y=-1.374729636998602*%i-0.7937005259840997],[x=1.587400917813934,y=1.259921095381759],[x=-1.374729636998603*%i-0.7937005259840998,y=1.091123635971721*%i-0.6299605249474366],[x=1.374729636998603*%i-0.7937005259840998,y=-1.091123635971721*%i-0.6299605249474366]] Результат решенной системы в программе maxima№6 algsys([y^3+z^3-7*x^3, y-z-3*x, z-x-y+2], [x,y,z]);[[x=1/2,y=1,z=-1/2],[x=1/2,y=(sqrt(111)*%i+5)/8,z=(sqrt(111)*%i-7)/8],[x=1/2,y=-(sqrt(111)*%i-5)/8,z=-(sqrt(111)*%i+7)/8]]№7 algsys([x^2+3*x*y+y^2-61, x*y-12], [x,y]);[[x=-3,y=-4],[x=-4,y=-3],[x=4,y=3],[x=3,y=4]]№8 algsys([x^3+y^3-6, x*y-2],](/img/thumbs/bac27e2f7f535caed6c17f676c6bb982-800x.jpg)