криволинейной трапеции«Первообразная. Интеграл. Площадь криволинейной трапеции»
10-11 классы
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и началам анализа на тему Первообразная. Интеграл. Площадь криволинейной трапеции (10-11 классы)
Содержание
- 1. Презентация по алгебре и началам анализа на тему Первообразная. Интеграл. Площадь криволинейной трапеции (10-11 классы)
- 2. Содержание1. Первообразная.1.1. Таблица первообразных.1.2. Справочный материал.1.3. Правило
- 3. Первообразная
- 4. Таблица первообразных
- 5. Функция F называется первообразной для
- 6. Правило нахождения первообразнойЕсли F есть первообразная для
- 7. Образцы решения 1.Найдите общий вид первообразных для
- 8. 2. Найдите для функции первообразную, график которой
- 9. Интеграл
- 10. Дата рождения: 4 января 1643 годаМесто рождения: Вулсторп (графство
- 11. Дата рождения: 1 июля 1646Место рождения: Лейпциг, ГерманияДата смерти: 14
- 12. Если f- непрерывная на [a;в], а F
- 13. Алгоритм вычисления интеграловНайдите первообразную F(x) подынтегральной функции
- 14. Образцы решения
- 15. Площадь криволинейной трапеции
- 16. Справочный материалПусть F(x) непрерывная и неотрицательная на
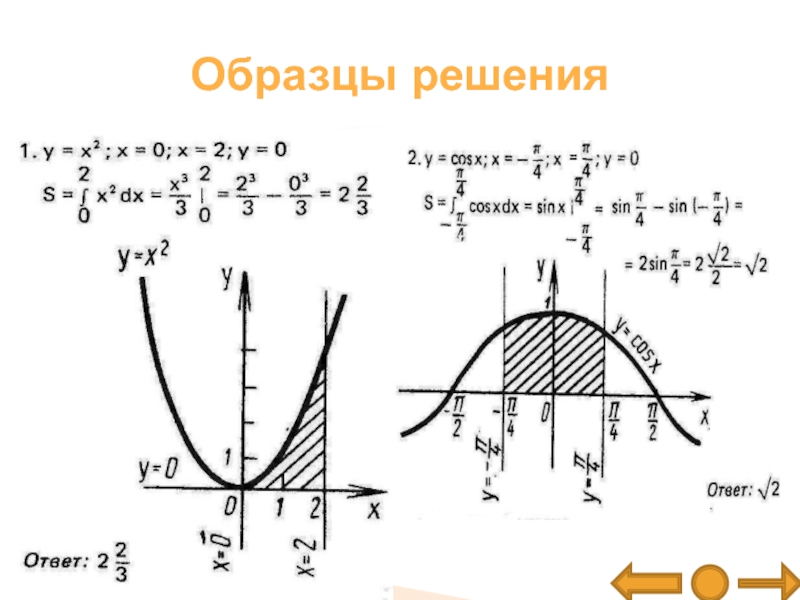
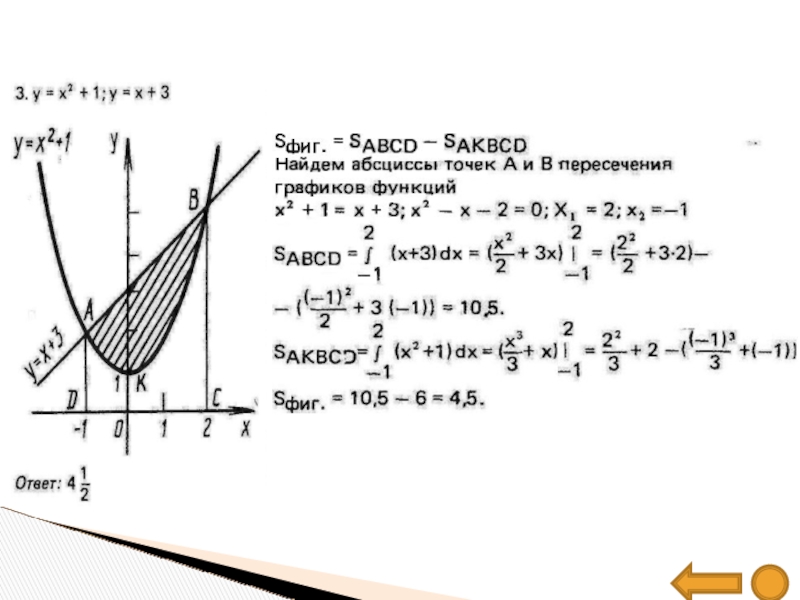
- 17. Образцы решения
- 18. Слайд 18
Содержание1. Первообразная.1.1. Таблица первообразных.1.2. Справочный материал.1.3. Правило нахождения.1.4. Образцы решения.2. Интеграл.2.1. Исаак Ньютон.2.2. Готфрид Вильгельм фон Лейбниц.2.3. Справочный материал.2.4. Алгоритм вычисления интегралов. 2.5. Образцы решения.3. Площадь криволинейной трапеции.3.1. Справочный материал.3.2. Образцы решения.
Слайд 1Презентация по алгебре и началам анализа на тему:
«Первообразная.«Первообразная. Интеграл.«Первообразная. Интеграл. Площадь
Слайд 2Содержание
1. Первообразная.
1.1. Таблица первообразных.
1.2. Справочный материал.
1.3. Правило нахождения.
1.4. Образцы решения.
2. Интеграл.
2.1.
Исаак Ньютон.
2.2. Готфрид Вильгельм фон Лейбниц.
2.3. Справочный материал.
2.4. Алгоритм вычисления интегралов.
2.5. Образцы решения.
3. Площадь криволинейной трапеции.
3.1. Справочный материал.
3.2. Образцы решения.
2.2. Готфрид Вильгельм фон Лейбниц.
2.3. Справочный материал.
2.4. Алгоритм вычисления интегралов.
2.5. Образцы решения.
3. Площадь криволинейной трапеции.
3.1. Справочный материал.
3.2. Образцы решения.
Слайд 5 Функция F называется первообразной для функции f на заданном
промежутке, если для всех х из этого промежутке F' (x)=f (x).
a) Функция есть первообразная для на промежутке (-∞ ; +∞), так как
б) Функция F(x)=sin x–8 есть первообразная для f(x)=cos x на промежутке (-∞ ; +∞), так как F'(x)=(sinx – 8)'=cosx=f(x).
a) Функция есть первообразная для на промежутке (-∞ ; +∞), так как
б) Функция F(x)=sin x–8 есть первообразная для f(x)=cos x на промежутке (-∞ ; +∞), так как F'(x)=(sinx – 8)'=cosx=f(x).
Справочный материал
Слайд 6Правило нахождения первообразной
Если F есть первообразная для f, а G –
первообразная для g, то F+G есть первообразная для f+g.
Если F есть первообразная для f, a k – постоянная, то kF есть первообразная для kf.
Если F(x) есть первообразная для f(x), а к и в – постоянные, причем к ≠ 0, то 1/к F (кх+в) есть первообразная для функции f (кх+в).
Если F есть первообразная для f, a k – постоянная, то kF есть первообразная для kf.
Если F(x) есть первообразная для f(x), а к и в – постоянные, причем к ≠ 0, то 1/к F (кх+в) есть первообразная для функции f (кх+в).
Слайд 7Образцы решения
1.Найдите общий вид первообразных для функций:
а)
(правило 1)
б) f(x)=5cosx; F(x)=5sinx+C
(правило 2)
в)
(правило 3)
г)
(правило 4)
б) f(x)=5cosx; F(x)=5sinx+C
(правило 2)
в)
(правило 3)
г)
(правило 4)
Слайд 82. Найдите для функции
первообразную, график которой проходит через точку М
(1;2).
С находим из условия F(1)=2.
Ответ:
С находим из условия F(1)=2.
Ответ:
Слайд 10Дата рождения:
4 января 1643 года
Место рождения:
Вулсторп (графство Линкольншир)
Дата смерти:
31 марта 1727
года
Место смерти:
Лондон, Англия
Научная сфера:
физика, математика, астрономия
Место смерти:
Лондон, Англия
Научная сфера:
физика, математика, астрономия
Исаак Ньютон
Слайд 11Дата рождения:
1 июля 1646
Место рождения:
Лейпциг, Германия
Дата смерти:
14 ноября 1716
Место смерти:
Ганновер, Германия
Научная
сфера:
Метафизика, эпистемологя, наука, математика, теодицея.
Метафизика, эпистемологя, наука, математика, теодицея.
Готфрид Вильгельм фон Лейбниц
Слайд 12Если f- непрерывная на [a;в], а F – первообразная
для f на
этом промежутке, то
(Формула Ньютона – Лейбница)
F(в)-F(а) есть приращение функции F на [а;в].
Сокращенно записывается
(Формула Ньютона – Лейбница)
F(в)-F(а) есть приращение функции F на [а;в].
Сокращенно записывается
Справочный материал
![Если f- непрерывная на [a;в], а F – первообразнаядля f на этом промежутке, то (Формула Ньютона –](/img/thumbs/dd78083e034e57e1a89ca517b0e2866d-800x.jpg "Презентация по алгебре и началам анализа на тему Первообразная. Интеграл. Площадь криволинейной трапеции (10-11 классы) Если f- непрерывная на [a;в], а F – первообразнаядля f на")
Слайд 13Алгоритм вычисления интегралов
Найдите первообразную F(x) подынтегральной функции f(x).
Найдите приращение первообразной на
[a;b]. Для этого найдите значение первообразной в точке b и вычтите из него значение первообразной в точке а.
Запишите ответ.
Запишите ответ.
![Алгоритм вычисления интеграловНайдите первообразную F(x) подынтегральной функции f(x).Найдите приращение первообразной на [a;b]. Для этого найдите значение первообразной](/img/thumbs/5e3875a03a38033872d6e236b3481b4f-800x.jpg "Презентация по алгебре и началам анализа на тему Первообразная. Интеграл. Площадь криволинейной трапеции (10-11 классы) Алгоритм вычисления интеграловНайдите первообразную F(x) подынтегральной функции f(x).Найдите приращение первообразной на")
Слайд 16Справочный материал
Пусть F(x) непрерывная и неотрицательная на отрезке [a;b]функция, S –
площадь соответствующей криволинейной трапеции. Если F есть первообразная для f на [a;b], то
![Справочный материалПусть F(x) непрерывная и неотрицательная на отрезке [a;b]функция, S – площадь соответствующей криволинейной трапеции. Если F](/img/thumbs/1f33350b66ee21c4f4a4b924332a3872-800x.jpg "Презентация по алгебре и началам анализа на тему Первообразная. Интеграл. Площадь криволинейной трапеции (10-11 классы) Справочный материалПусть F(x) непрерывная и неотрицательная на отрезке [a;b]функция, S –")
