- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и начала анализа на тему Показательная функция. Решение показательных неравенств (10 класс)
Содержание
- 1. Презентация по алгебре и начала анализа на тему Показательная функция. Решение показательных неравенств (10 класс)
- 2. 2.Основные свойства показательной функции. (5минут) (фронтальная работа с классом)1ху0у=ах при 0
- 3. 3.Устная работа по решению простейших задач
- 4. 2) На рисунке изображён график одной из функций.Укажите номер этой функции.ху011 1.у=-(1/2)х2.у=-log2x3.y=-2x4.y= log1/2x
- 5. 3)Указать характер монотонности функций:а)у=5х, б)у=(1/2)х; в)у=(√5)х; г)у=(tgπ/3)х;д)у=(sin 30°)х; е)у=( tg80°)х
- 6. 4)Найти область определения функции: а) у=32/х-2; б)у=(1/6)1/х
- 7. 5) Какое число не входит в множество
- 8. 4.Повторение теоретического материала по теме«Решение показательных неравенств»
- 9. хух1х2ах1ах2а>1х1< х2ах1< ах2у-возрастаетх1х2ах1ах2х1< х2ах1 > ах2у-убываетху0
- 10. 3.Показательное неравенство аf(x) > a g(x)
- 11. б) ( 0,1)5х-9 < 0,001 Решение. ( 0,1)5х-9 12х >12/5х >2,4Ответ: х >2,4.Подведение итога.Д/з: п.45, №
- 12. Х2+2х
- 13. г)3х+1·21-х+33·2-х
- 14. д)22х+2>6х+2·32х+2Решение.22х+2>6х+2·32х+2Разделим обе части неравенства на 32х22х+2
- 15. Разноуровневая самостоятельная работа (15 минут)Каждый получает карточку
- 16. 2-я группаКарточка №1а)Решить неравенство: (5)7-2х
- 17. 3-я группа.а)Решите неравенство 0,52х-1>0,253х+21)(4;+∞)
- 18. Подведение итогов, выставление оценок.Д/3: п.42, № 40.44-40.46 (в,г)
Слайд 1Тема урока:
Обобщающий урок по теме «Показательная функция. Решение
10 класс
Слайд 22.Основные свойства показательной функции. (5минут)
(фронтальная работа с классом)
1
х
у
0
у=ах при 0
1.Область определения
D(y)=(─∞;∞)
2.Множество значений
Е(у)=(0;∞)
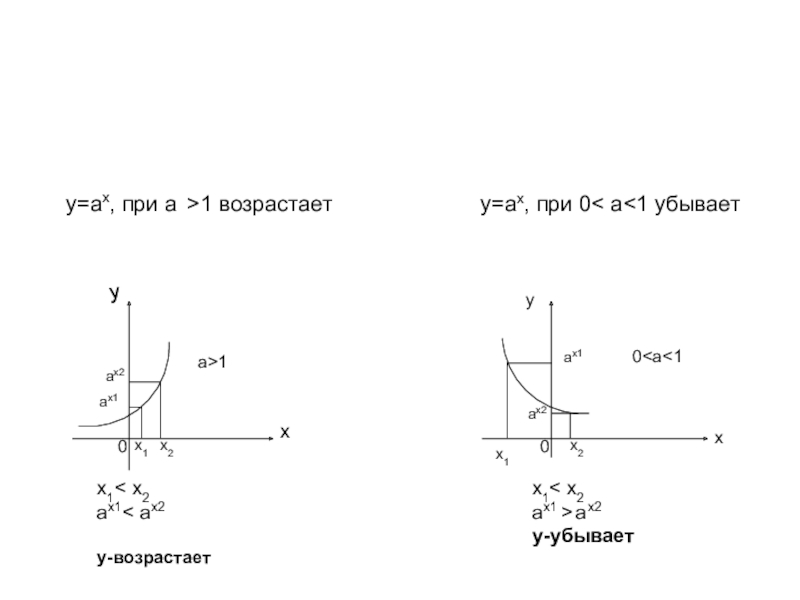
3.Если 0<а<1,
то у убывает на D(y)
1.Область определения
D(y)=(─∞;∞)
2.Множество значений
Е(у)=(0;∞)
3.Если а>1,
то у возрастает на D(y)
График функции у=ах проходит через точку с координатами (0;1)
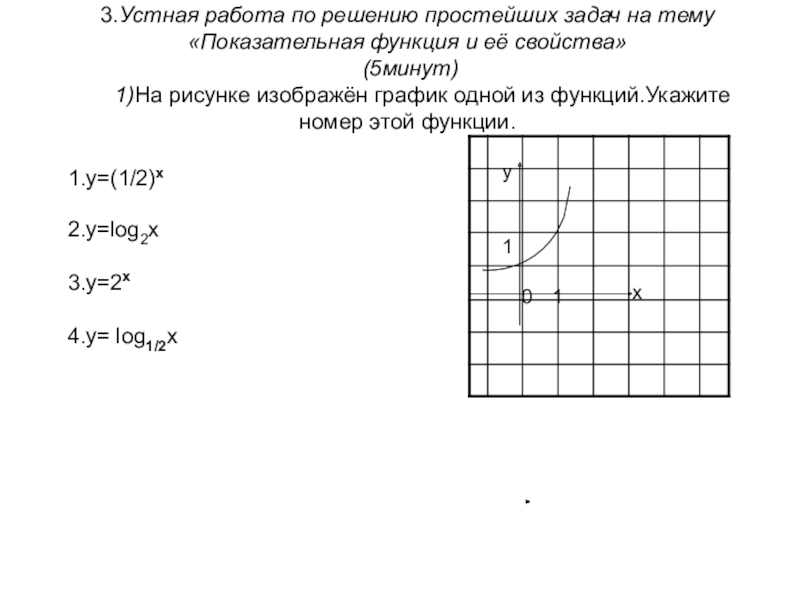
Слайд 3 3.Устная работа по решению простейших задач на тему «Показательная функция и
х
у
0
1
1
1.у=(1/2)х
2.у=log2x
3.y=2x
4.y= log1/2x
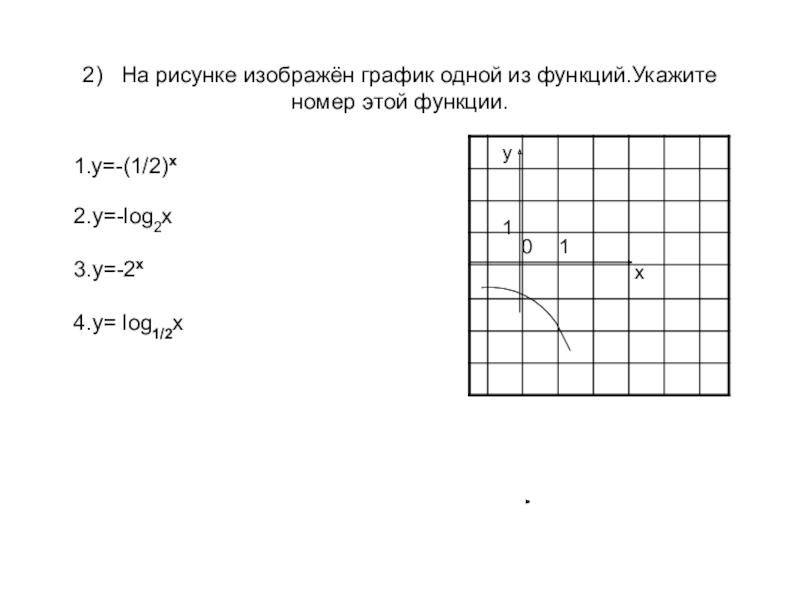
Слайд 4 2) На рисунке изображён график одной из функций.Укажите номер этой
х
у
0
1
1
1.у=-(1/2)х
2.у=-log2x
3.y=-2x
4.y= log1/2x
Слайд 53)Указать характер монотонности функций:
а)у=5х, б)у=(1/2)х; в)у=(√5)х;
д)у=(sin 30°)х; е)у=( tg80°)х
Слайд 75) Какое число не входит в множество значений функции?
f(x)=(5/2)x – 1
1)2 2)-1 3)0 4)-0,5
6) Найдите наименьшее целое значение функции
у=ех+1
1)0 2)1 3)-1 4)2
Слайд 84.Повторение теоретического материала по теме
«Решение показательных неравенств» (10 минут)
(фронтальная работа)
1.Какие
Это неравенства вида аf(x)>аg(x),где а >0,а≠1, и неравенства, сводящиеся к этому виду.
2. Какие свойства показательной функции используются при этом?
Неравенства решаются с помощью свойств возрастания и убывания показательной функции.
Слайд 103.Показательное неравенство аf(x) > a g(x) равносильно неравенству того же
Показательное неравенство аf(x) > a g(x) равносильно неравенству противоположного смысла f(x)
4.Работа в группах под руководством консультанта-ученика (с последующей проверкой) 10 минут
Решить неравенство а) 2 3х+7 <2 2х-1
Решение.
2 3х+7 <2 2х-1, 2>1, неравенство равносильно неравенству того же смысла
3х+7 <2х-1
3х-2х < -7-1
х <-8. Ответ: х<-8.
Слайд 11б) ( 0,1)5х-9 < 0,001
Решение.
( 0,1)5х-9
5х-9>3
5х >12
х >12/5
х >2,4
Ответ: х >2,4.
Подведение итога.
Д/з: п.45, №
Слайд 12 Х2+2х 3
в)6
Решение.
Это неравенство равносильно неравенству того же смысла (т.к.6>1)
х2+2х > 3
х2+2х -3>0
Корни квадратного трёхчлена х2+2х -3:
х1=-3, х2=1
Построим схематически параболу у=х2+2х-3
-3
1
х
Решение неравенства х2+2х -3 >0:
х<-3, х >1.
Ответ: х<-3; х >1.
Слайд 13
г)3х+1·21-х+33·2-х
7·3х 21
2х 2
3х 3
2х 2
3 Х 3 1 3
2 2 2
+
1, неравенство равносильно неравенству
того же смысла
х<1
Ответ: х<1
Слайд 14
д)22х+2>6х+2·32х+2
Решение.
22х+2>6х+2·32х+2
Разделим обе части неравенства на 32х
22х+2 6х
32х 32х 32х
2 2х х х
3
·4-
2
3
-18>0, пусть 2
3
=t, где t>0
4(t+2) (t-9/4)>0
С учётом t>0,получим:
9/4
t
t
t>9/4
2 х
3
2 Х -2
3
9
4
2
3
,2
3
1, поэтому х‹-2. Ответ: х‹-2.
0
-2
Слайд 15
Разноуровневая самостоятельная работа (15 минут)
Каждый получает карточку с заданиями.
1-я группа (слабомотивированные
Карточка №1
а)2х≥4
1)[2;+∞) 2)(-∞;2] 3) (-4;+∞) 4) [4;+∞)
б)5 5-х >25
1)(-3;+∞) 2) )(-∞;3) 3)(-∞;-20) 4) (3;+∞)
в)Расположите числа в порядке возрастания: 21/2,2-0,2,23,2-1
1) 21/2,2-0,2,23,2-1; 2) 21/2,2-0,2,2-1,23; 3)2-1;2-0,2;21/2; 4) 2-0,2,2-1,23; 21/2.
г).Укажите множество значений функции у=(1/5)х-4
1) (4;+∞) 2) (-4;+∞) 3) [-4;+∞) 4) (-∞;-4)
д).Укажите характер монотонности функции у=(3)х
1)убывает 2)возрастает 3)ни возрастает ни убывает
е).Найдите область определения функции у=1/2х
1)(0;+∞) 2)(1/2;+∞) 3) [0;+∞) 4) [1/2;+∞)
Слайд 162-я группа
Карточка №1
а)Решить неравенство: (5)7-2х
в)Найдите область определения функции у=(х+2)/(0,5х-2)
г)Решить неравенство: 2х+2х+2≤ 20
д)Укажите характер монотонности функции у=(1/π)х
е)Найдите наибольшее и наименьшее значения функции
у=3х-1+8 на отрезке [-3;1].
Слайд 173-я группа.
а)Решите неравенство 0,52х-1>0,253х+2
1)(4;+∞)
б)Решите неравенство х·42х-1+16·42х-1>0
1)(16;+∞) 2)(1/2;+∞) 3)(-16;+∞) 4)(- ∞;-16)
√32х+7-27
в)Укажите область определения функции у=
х
1)[-2;0) (0 ;+∞); 2) (-2;+∞); 3) )[-2;+∞); 4) (- ∞;-2)
г)Найти на каком отрезке функция у=2х принимает наибольшее значение, равное 32, и наименьшее, равное ½.
1)[-5;-1] 2)[-1;5] 3)(-1;5) 4)(-5;-1)
д)Укажите число, не принадлежащее множеству значений функции
sin2x+1
y=(1/4); 1)1/4; 2)1/8; 3)1/16; 4)1.
е)Найти решение неравенства: 5√2х+1 +5< 5√2х+1 +1+ 5√2х+1
(подробное решение)











![Презентация по алгебре и начала анализа на тему Показательная функция. Решение показательных неравенств (10 класс) Разноуровневая самостоятельная работа (15 минут)Каждый получает карточку с заданиями.1-я группа (слабомотивированные Разноуровневая самостоятельная работа (15 минут)Каждый получает карточку с заданиями.1-я группа (слабомотивированные учащиеся)Карточка №1а)2х≥41)[2;+∞) 2)(-∞;2]](/img/thumbs/4d88e380dcbc40e0cfd204fb2f9aa4f4-800x.jpg)








