- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре и математическому анализу на тему Производная функции (10 класс)
Содержание
- 1. Презентация по алгебре и математическому анализу на тему Производная функции (10 класс)
- 2. f ' (x0) = lim (∆
- 3. Если функция у = f (х)
- 4. Правило №1 Если функции u и v
- 5. Правило №3 Если функции и
- 6. С помощью производной функции устанавливают промежутки монотонности,
- 7. Определение. Внутренняя точка области определения, в которой
- 8. Правило нахождения наибольшего и наименьшего значения функции
- 9. 1. Область определения; 2. Область значения;
- 10. Пример №1. Построить график функцииf(x) = x3
- 11. 0f(x)- 227. Нужно решить неравенство: 3
- 12. Слайд 12
Слайд 2 f ' (x0) = lim (∆ f / ∆x)
Пусть х - произвольная точка, лежащая в некоторой окрестности точки Х0 (окрестность точки Х0 - это интервал (а; b), Х0 (а; b)).
Разность х- Х0 называется приращением аргумента:
∆x = х- Х0. Отсюда x = Х0 + ∆x.
Разность f(x)-f(Х0 ) называется приращением функции:
∆f = f(x) - f(x0) или
∆ f = f(x0+∆x) – f(x0).
Отсюда
f (x0 +∆x) = f (x0 ) + ∆ f.
Рис.1
Определение производной
Геометрический смысл приращений ∆х и ∆ f показан на рис.1.
Производной функции y = f(x) в точке x0 называется предел отношения приращения функции ∆f к приращению аргумента ∆x, стремящегося к "нулю“.
Обозначается f ' (x0).
Итак,
Слайд 3 Если функция у = f (х) имеет производную в точке
Нахождение производной данной функции называется дифференцированием.
Слайд 4Правило №1
Если функции u и v дифференцируемы в точке x0,
( + )'=' + '
Правило №2
Если функции u и v дифференцируемы в точке x0, то их произведение также дифференцируемо в точке x0, причем
( ∙ )' = ' + '
Правила дифференцирования
Слайд 5Правило №3
Если функции и дифференцируемы в точке х0
(/)' = (' - ') / ²
Правило №4
Если функция u дифференцируема в точке x0 и с = const, то их произведение также дифференцируемо в точке x0 , причем
(сu)' = сu'.
Правило №5
Если f (g(х)) - сложная функция, то ее производная равна произведению производных внешней и внутренней функций, т.е.
[f(g(x))]'= f '(g) ◦ g'(x)
Правила дифференцирования
Слайд 6С помощью производной функции устанавливают промежутки монотонности, точки экстремума, наибольшее и
При этом используются следующие теоремы:
Теорема №1
Если f ' (х) > 0 в каждой точке интервала I, то функция возрастает на I. Если f ' (х) < 0 в каждой точке интервала I, то функция убывает на I.
Теорема №2
Теорема Ферма (необходимое условие экстремума):
если x0- точка экстремума и в этой точке существует производная, то она равна нулю.
Слайд 7Определение.
Внутренняя точка области определения, в которой производная равна нулю или
Теорема №3
Достаточное условие экстремума:
если функция f (x) непрерывна в точке x0, а f '(х) > 0 на интервале (а; x0) и
f '(х) < 0 на интервале (x0; b), то точка x0 является точкой максимума.
Обозначается Xmax
Слайд 8Правило нахождения наибольшего и наименьшего значения функции на [а; b]:
а) убедиться,
б) найти критические точки, принадлежащие [а; b];
в) вычислить значения функции в этих точках и на концах отрезка;
г) сравнением установить наибольшее и наименьшее значение,
обозначается max f(X) = f(X1), min f(X) = f(X2)
[а; b ] [а; b]
Примечания
1. Если рассматривают функцию не на отрезке, а на интервале (а; b), то вычисляют вместо значений функции на концах пределы
lim f(x) и lim f(x). x→а х→b
2. Не следует путать наименьшее и наибольшее значение функции с минимумом и максимумом функции.
С помощью пределов исследуют "поведение" функции на бесконечности, а также вблизи точек разрыва, устанавливают наличие асимптот.
Слайд 9 1. Область определения;
2. Область значения;
3. Чётность (нечётность);
4.
5. Координаты точек пересечения графика с осью Ох;
6. Координаты точек пересечения графика с осью Оу;
7. Промежутки возрастания графика функции;
8. Промежутки убывания графика функции;
9. Точки минимума и максимума функции;
10. Значение функции в точках минимума и максимума;
11. Дополнительные точки (если они нужны).
Схема исследования функций
для построения её графика
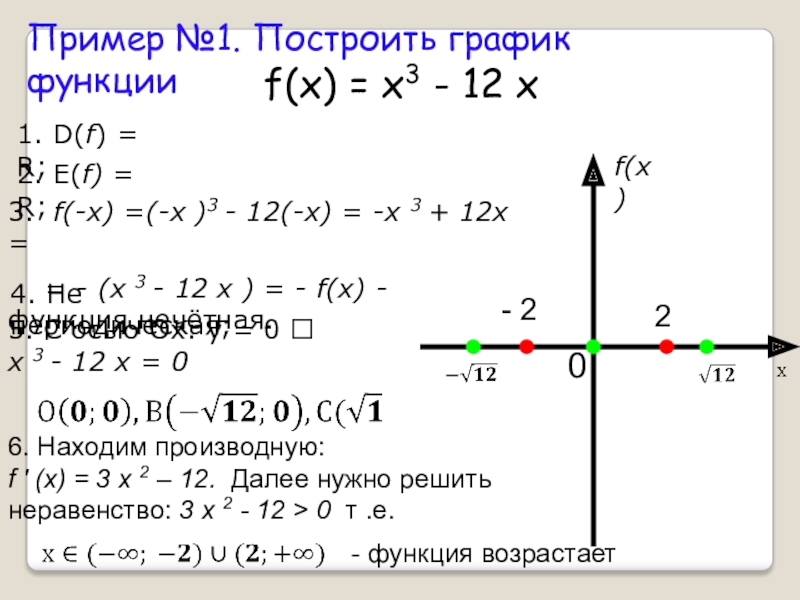
Слайд 10Пример №1. Построить график функции
f(x) = x3 - 12 x
1.
2. E(f) = R;
f(x)
0
3. f(-x) =(-x )3 - 12(-x) = -x 3 + 12x =
= - (x 3 - 12 x ) = - f(x) - функция нечётная.
4. Не периодическая;
5. С осью Ох: у = 0
x 3 - 12 x = 0
6. Находим производную: f ' (x) = 3 x 2 – 12. Далее нужно решить неравенство: 3 x 2 - 12 > 0 т .е.
- 2
2
- функция возрастает
Слайд 110
f(x)
- 2
2
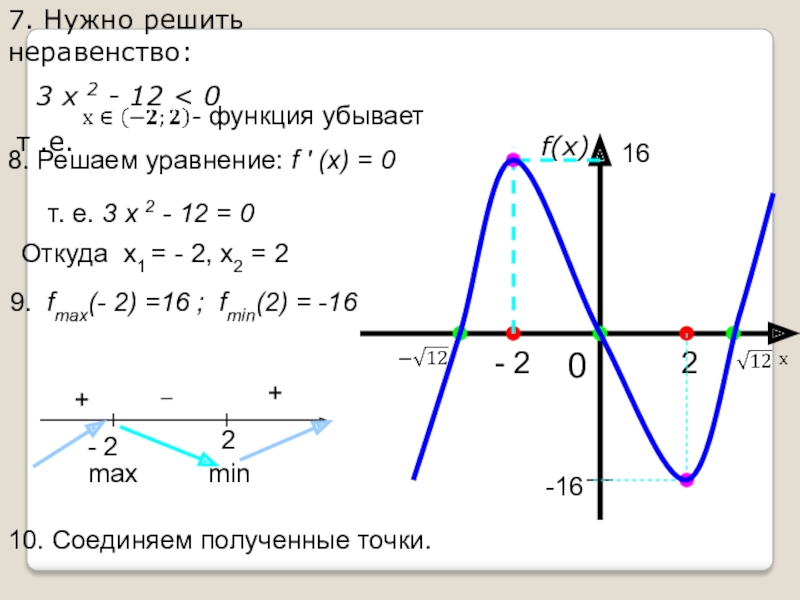
7. Нужно решить неравенство:
3 x 2 - 12
т .е.
8. Решаем уравнение: f ' (x) = 0
т. е. 3 x 2 - 12 = 0
Откуда х1 = - 2, х2 = 2
- 2
2
_
max
min
9. fmax(- 2) =16 ; fmin(2) = -16
16
-16
10. Соединяем полученные точки.
+
+
- функция убывает







![Презентация по алгебре и математическому анализу на тему Производная функции (10 класс) Правило нахождения наибольшего и наименьшего значения функции на [а; b]:а) убедиться, Правило нахождения наибольшего и наименьшего значения функции на [а; b]:а) убедиться, что функция у = f(x) непрерывна](/img/thumbs/14132b3dbd21307f3072bb086ab52bfc-800x.jpg)