- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Экстремумы функции
Содержание
- 1. Презентация по алгебре Экстремумы функции
- 2. Максимум функцииf(х)y=f(x)
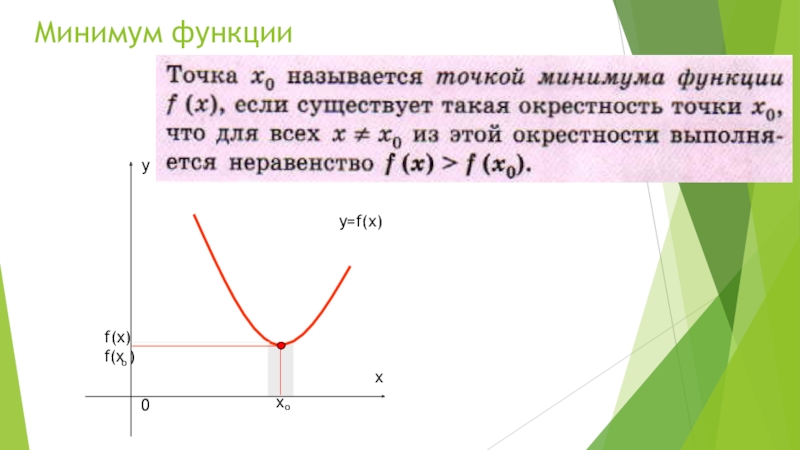
- 3. Минимум функцииf(х)y=f(x)
- 4. Точки минимума и максимуманазываются точками экстремума функции.
- 5. Точки, в которых производная функции равна 0,
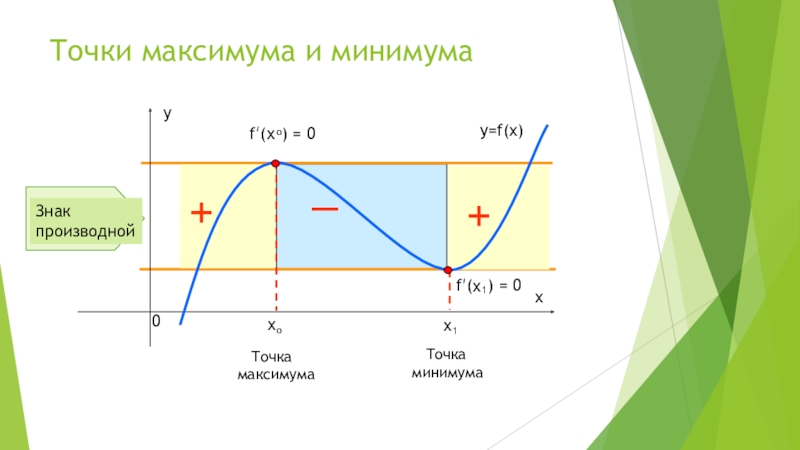
- 6. Точки максимума и минимума_ Точка максимума Точка минимума
- 7. Точки, в которых функция имеет производную, равную
- 8. На рисунке изображён график дифференцируемой функции y=f(x), определённой
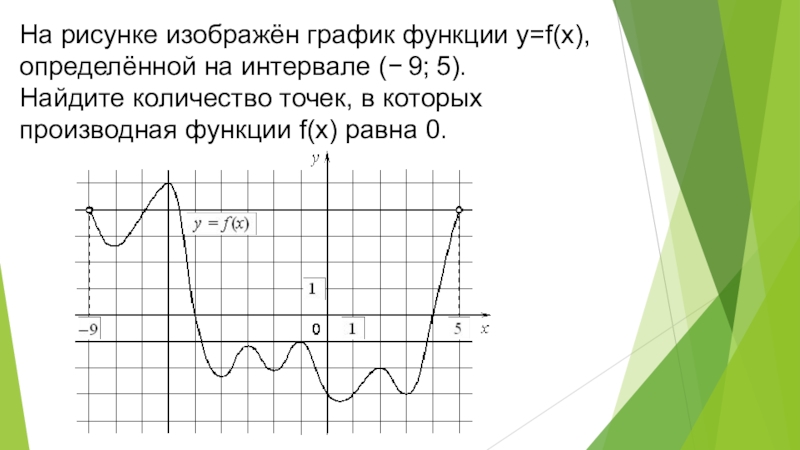
- 9. На рисунке изображён график функции y=f(x), определённой на
- 10. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].
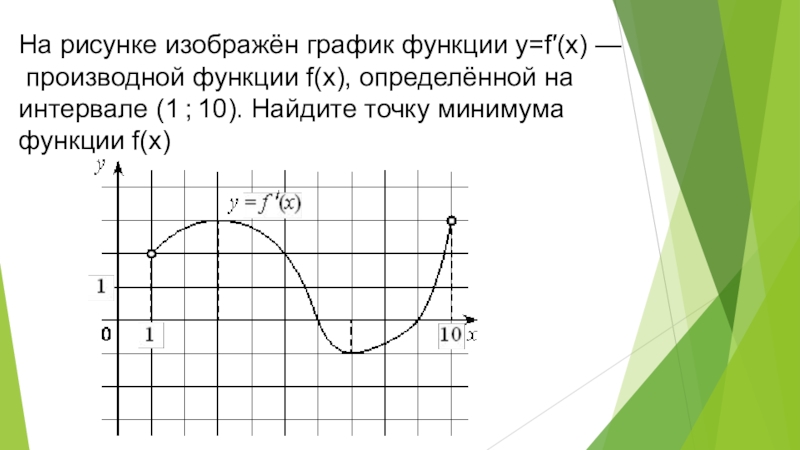
- 11. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (1 ; 10). Найдите точку минимума функции f(x)
- 12. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 5 ; 5). Найдите точку максимума функции f(x).
- 13. На рисунке изображён график y = f '(x) — производной функции f(x),
- 14. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3 ; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 2 ; 15].
- 15. 1)функция возрастает на отрезке [− 1; 1]2)функция убывает на отрезке [− 1; 1]3)функция
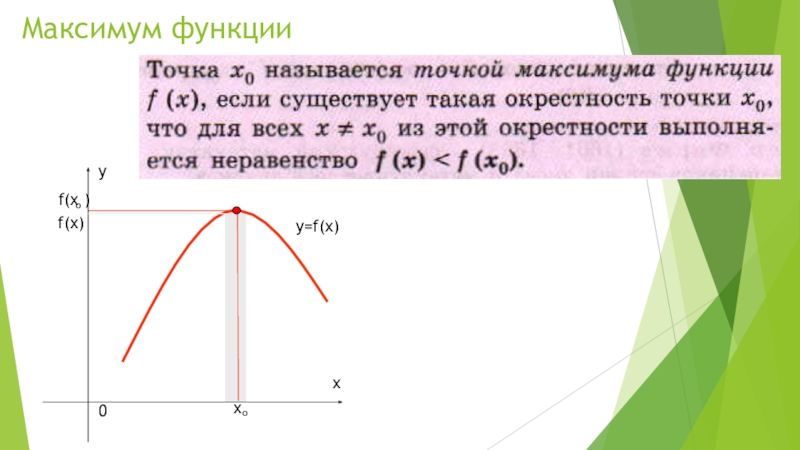
Максимум функцииf(х)y=f(x)
Слайд 4Точки минимума и максимума
называются точками экстремума функции.
Если х0 - точка
экстремума
дифференцируемой функции f(х),
то производная функции в
этой точке f'(х0) = 0. Необходимый признак экстремума (теорема Ферма)
дифференцируемой функции f(х),
то производная функции в
этой точке f'(х0) = 0. Необходимый признак экстремума (теорема Ферма)
Слайд 5Точки, в которых производная функции равна 0, называют стационарными точками.
х=0
– точка , в которой производная равна 0, но она не является точкой экстремума.
Слайд 7Точки, в которых функция имеет производную, равную 0 или не имеет
производной, называют критическими точками.
х=0 – точка минимума, а производной в этой точке нет.
Слайд 8На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (2 ; 13).
Найдите точку
из отрезка [8 ; 12],
в которой производная функции f(x) равна 0.
Слайд 9На рисунке изображён график функции y=f(x),
определённой на интервале (− 9; 5).
Найдите количество точек,
в которых
производная функции f(x) равна 0.
производная функции f(x) равна 0.
Слайд 10На рисунке изображён график y=f′(x) —
производной функции f(x), определённой
на интервале (−9; 8). Найдите точку экстремума
функции f(x) на отрезке [−3; 3].
Слайд 11На рисунке изображён график функции y=f′(x) —
производной функции f(x), определённой на
интервале (1 ; 10). Найдите точку
минимума
функции f(x)
Слайд 12На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 5 ; 5). Найдите точку
максимума функции f(x).
Слайд 13На рисунке изображён график y = f '(x) —
производной функции f(x), определённой на
интервале (− 11 ; 6). Найдите
количество точек
минимума функции f(x), принадлежащих
отрезку [− 6 ; 4].
минимума функции f(x), принадлежащих
отрезку [− 6 ; 4].
Слайд 14На рисунке изображён график y=f '(x) —
производной функции f(x), определённой на
интервале (− 3 ; 19). Найдите количество точек
максимума функции f(x), принадлежащих
отрезку [− 2 ; 15].
Слайд 151)функция возрастает на отрезке [− 1; 1]
2)функция убывает на отрезке [− 1; 1]
3)функция имеет точку минимума на
отрезке [− 1; 1]
4)функция имеет точку максимума на отрезке [− 1; 1]
4)функция имеет точку максимума на отрезке [− 1; 1]
А)
Б)
В)
Г)




![Презентация по алгебре Экстремумы функции На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (2 ; 13). Найдите точку На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (2 ; 13). Найдите точку из отрезка [8 ; 12], в которой производная функции f(x) равна](/img/thumbs/868894285f1e15c4bea015ce41d862c7-800x.jpg)
![Презентация по алгебре Экстремумы функции На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3]. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].](/img/thumbs/33acb712dfaa6fc73491f555de9c9acf-800x.jpg)

![Презентация по алгебре Экстремумы функции На рисунке изображён график y = f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите На рисунке изображён график y = f '(x) — производной функции f(x), определённой на интервале (− 11 ; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 6 ; 4].](/img/thumbs/b5b981b8f77b227ab788685af4060391-800x.jpg)
![Презентация по алгебре Экстремумы функции На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3 ; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 2 ; 15]. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 3 ; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 2 ; 15].](/img/thumbs/d1d308a1ce03918ce014763c6edb451b-800x.jpg)
![Презентация по алгебре Экстремумы функции 1)функция возрастает на отрезке [− 1; 1]2)функция убывает на отрезке [− 1; 1]3)функция имеет точку минимума на 1)функция возрастает на отрезке [− 1; 1]2)функция убывает на отрезке [− 1; 1]3)функция имеет точку минимума на отрезке [− 1; 1]4)функция имеет точку максимума на отрезке [− 1; 1]А)Б)В)Г)](/img/thumbs/0047c5b177460aafb37e3f94bf0af3bb-800x.jpg)





