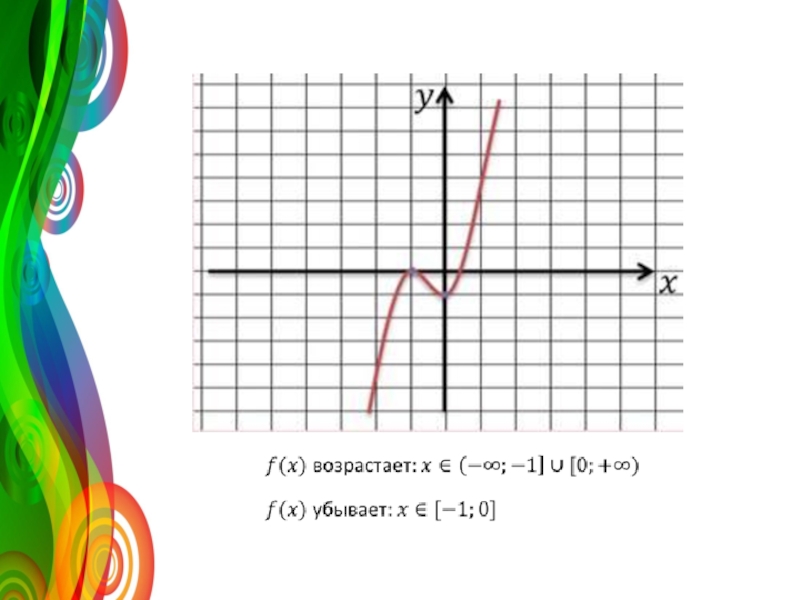- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Экстремум функции (10 класс)
Содержание
- 1. Презентация по алгебре Экстремум функции (10 класс)
- 2. Слайд 2
- 3. Посмотрим на точки (-1; 0) и (0;
- 4. Чем-то он похож на предыдущий график. В
- 5. ОпределениеТочку x = x1 называют точкой минимума
- 6. ОпределениеТочку x = x1 называют точкой максимума
- 7. Точки минимума и максимума функции объединяют общим
- 8. Теорема Если функция y = f (x)
- 9. Обратим внимание, что при переходе через точку
- 10. Теорема . Пусть функция y = f
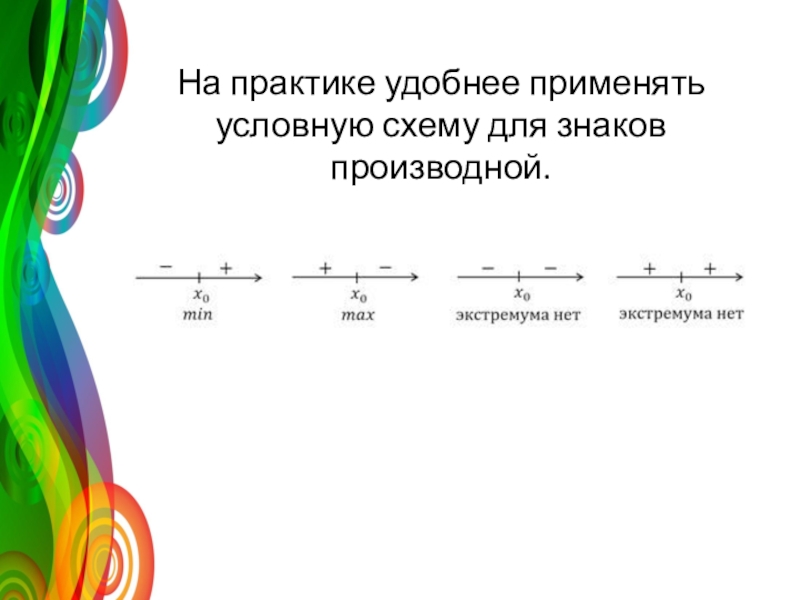
- 11. На практике удобнее применять условную схему для знаков производной.
- 12. Пример
- 13. Алгоритм исследования непрерывной функции y = f (x) на монотонность и экстремумы
- 14. Пример
- 15. Пример
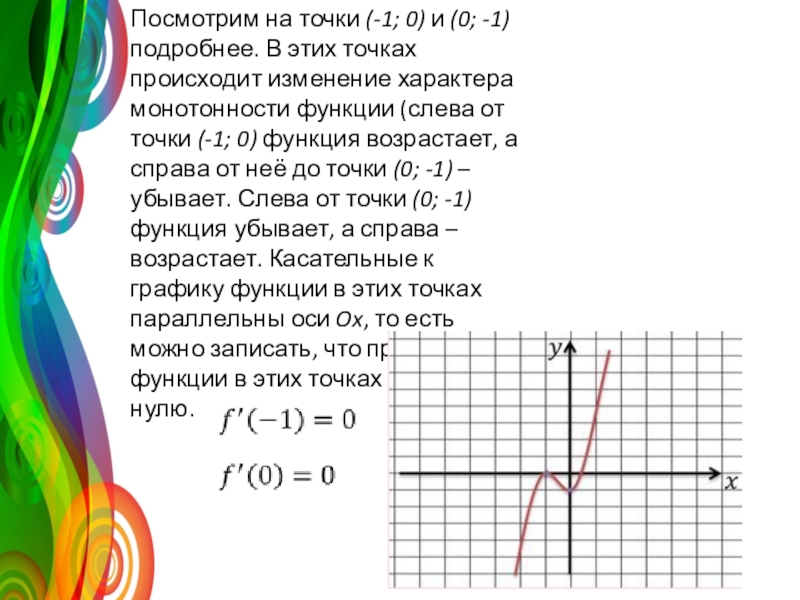
Слайд 3Посмотрим на точки (-1; 0) и (0; -1) подробнее. В этих
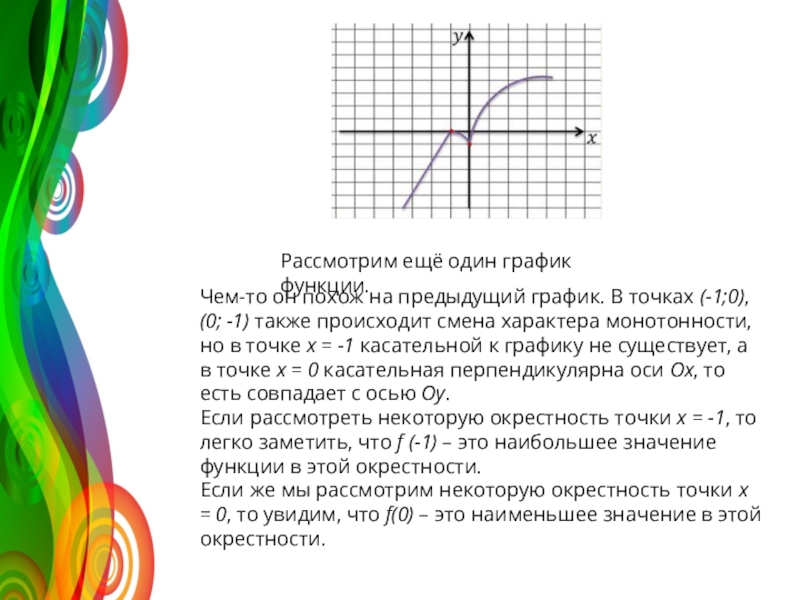
Слайд 4Чем-то он похож на предыдущий график. В точках (-1;0), (0; -1)
Если рассмотреть некоторую окрестность точки x = -1, то легко заметить, что f (-1) – это наибольшее значение функции в этой окрестности.
Если же мы рассмотрим некоторую окрестность точки x = 0, то увидим, что f(0) – это наименьшее значение в этой окрестности.
Рассмотрим ещё один график функции.
Слайд 5Определение
Точку x = x1 называют точкой минимума функции y = f(x),
Функции, графики которых мы построили, имеют точку минимума
x = 0. Потому что можно выбрать окрестность, например, (-1/2; ½) или (-0,2; 0,2), для всех точек которой выполняется неравенство f(x) ≥ f (0).
Значение функции в точке минимума обозначают ymin. Не будем путать это значение с наименьшим значением функции. Очевидно, что функции, графики которых изображены на рисунках, не имеют наименьших значений. А ymin существуют.
Слайд 6Определение
Точку x = x1 называют точкой максимума функции y = f(x),
Функции, графики которых мы построили, имеют точку максимума
x = -1. Потому что можно выбрать окрестность, например, (-3/2; -1/2), для всех точек которой выполняется неравенство f (x) ≤ f (-1). Это верно для обеих функций.
Значение функции в точке максимума обычно обозначают ymax. Не будем путать это значение с наибольшим значением функции. Очевидно, что функции, графики которых изображены на рисунках, не имеют наибольших значений. А ymax существует.
Слайд 7Точки минимума и максимума функции объединяют общим термином – точки экстремума
В математике исследование задач на максимум и минимум началось очень давно – двадцать пять веков назад, Долгое время к задачам на отыскание экстремумов не было сколько-нибудь единых подходов. Но примерно триста лет назад – в эпоху формирования математического анализа – были созданы первые общие методы решения и исследования задач на экстремум.
Большую работу в этом направлении проводили Ферма и Эйлер. Правила определения экстремумов функции одной переменной y = f (x) были даны Маклореном.
Слайд 8Теорема
Если функция y = f (x) имеет экстремум в точке
Внутренние точки области определения, в которых производная функции равна нулю, называют стационарными, а внутренние точки области определения, в которых функция непрерывна, но производная не существует, называют критическими.
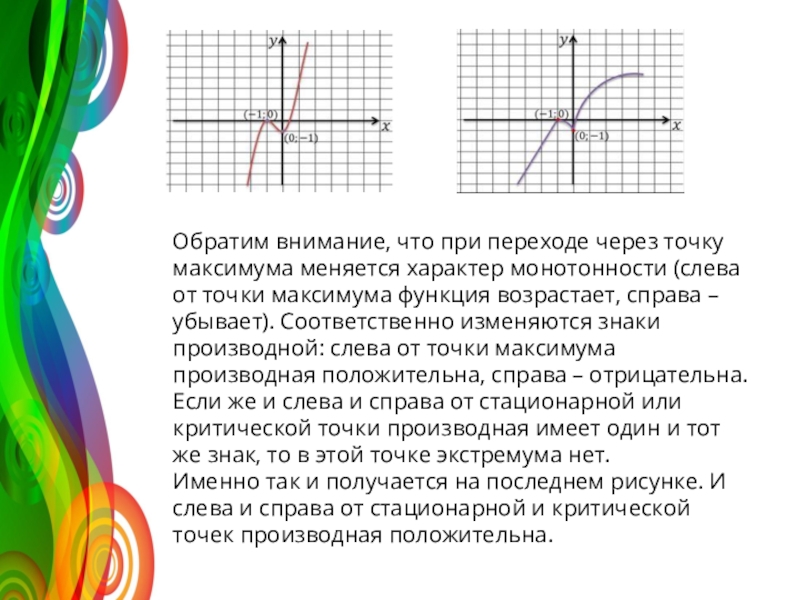
Слайд 9Обратим внимание, что при переходе через точку максимума меняется характер монотонности
Если же и слева и справа от стационарной или критической точки производная имеет один и тот же знак, то в этой точке экстремума нет.
Именно так и получается на последнем рисунке. И слева и справа от стационарной и критической точек производная положительна.