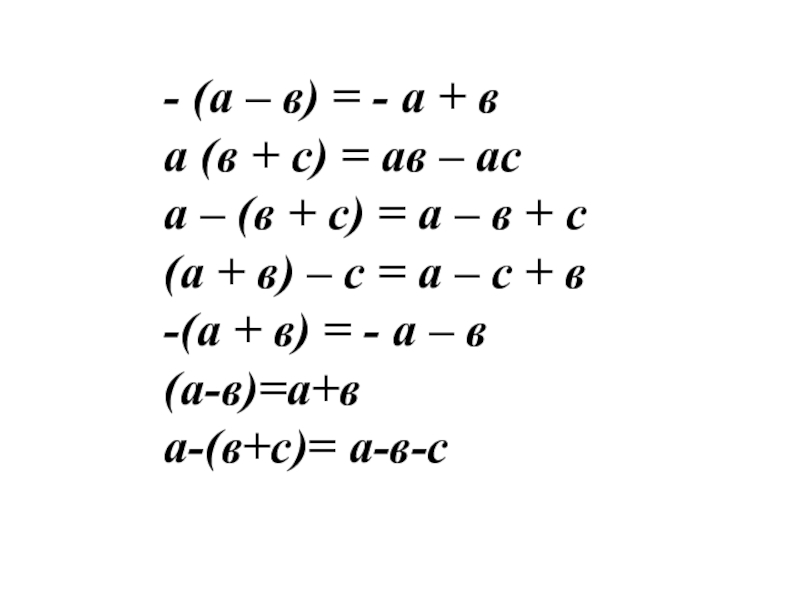у нас,
А сердце умным будет!»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре Доказательство тождеств
Содержание
- 1. Презентация по алгебре Доказательство тождеств
- 2. Доказательство тождеств
- 3. Найдем значение выражений при х=5 и
- 4. ВЫВОД:Мы получили один и тот же результат.
- 5. Рассмотрим теперь выражения 2х+у и 2ху. при
- 6. ВЫВОД:Выражения 3(х+у) и 3х+3у являются тождественно равными,
- 7. ТОЖДЕСТВОРавенство 3(х+у) и 3х+3у верно при любых
- 8. Тождествами являются равенства, выражающие основные свойства действий
- 9. а + 0 = аа *
- 10. Чтобы привести подобные слагаемые, надо сложить их
- 11. Если перед скобками стоит знак «плюс», то
- 12. Если перед скобками стоит знак «минус», то
- 13. - (а – в) = - а
- 14. Что необходимо сделать, чтобы доказать, что равенство является тождеством?
- 15. 10х(5х+4)=5х–45х –7 = 28х–3- х–4–22х(х-5)(х+2)= (х+4)(х–7)+18–(2х – 3)+ (х2 +2х –3)= х211х – 3= 2х +12 + 9х–15–4(3у – 1)+1 =–6(2у – 1) –1 Докажите тождество
- 16. Выписать левую часть равенства, ее преобразовать и
- 17. Самостоятельная работа 2*(у-1)=(-2у-2)даданетдада
- 18. Равенства всякие, братцы, бывают, И каждый об
- 19. Домашнее задание: №715, 745Спасибо за урок!
Доказательство тождеств
Слайд 3Найдем значение выражений
при х=5 и у=4
3(х+у)=
3(5+4)=3*9=27
3х+3у=
3*5+3*4=27
Найдем значение
выражений
при х=6 и у=5
3(х+у)=
3(6+5)=3*11=33
3х+3у=
3*6+3*5=33
3(х+у)=
3(6+5)=3*11=33
3х+3у=
3*6+3*5=33
Слайд 4ВЫВОД:
Мы получили один и тот же результат.
Из распределительного свойства следует,
что вообще при любых значениях переменных значения выражений 3(х+у) и 3х+3у равны.
3(х+у) = 3х+3у
3(х+у) = 3х+3у
Слайд 5Рассмотрим теперь выражения 2х+у и 2ху.
при х=1 и у=2
2х+у=2*1+2=4
2ху=2*1*2=4
принимают равные
значения:
при х=3, у=4
2х+у=2*3+4=10
2ху=2*3*4=24
значения выражений разные
при х=3, у=4
2х+у=2*3+4=10
2ху=2*3*4=24
значения выражений разные
Слайд 6ВЫВОД:
Выражения 3(х+у) и 3х+3у являются тождественно равными, а выражения 2х+у и
2ху не являются тождественно равными.
Определение:
Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Определение:
Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Слайд 7ТОЖДЕСТВО
Равенство 3(х+у) и 3х+3у верно при любых значениях х и у.
Такие равенства называются тождествами.
Определение: Равенство, верное при любых значениях переменных, называется тождеством.
Тождествами считают и верные числовые равенства. С тождествами мы уже встречались.
Определение: Равенство, верное при любых значениях переменных, называется тождеством.
Тождествами считают и верные числовые равенства. С тождествами мы уже встречались.
Слайд 8Тождествами являются равенства, выражающие основные свойства действий над числами.
a + b
= b + a
ab = ba
(a + b) + c = a + (b + c)
a(b + c) = ab + ac
Слайд 9
а + 0 = а
а * 1 = а
а + (-а)
= 0
а * (-b) = - ab
а-b = a + (-b)
(-a) * (-b) = ab
а * (-b) = - ab
а-b = a + (-b)
(-a) * (-b) = ab
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
Слайд 10Чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить
на общую буквенную часть;
Пример 1.
Приведем подобные слагаемые
5х +2х-3х=
х(5+2-3)=4х
Слайд 11Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив
знак каждого слагаемого, заключенного в скобки;
Пример 2.
Раскроем скобки в выражении
2а + (b-3c) =
2a + b – 3c
Слайд 12Если перед скобками стоит знак «минус», то скобки можно опустить, изменив
знак каждого слагаемого, заключенного в скобки.
Пример 3.
Раскроем скобки в выражении
а – (4b – с) =
a – 4b + c
Слайд 13- (а – в) = - а + в
а (в + с) = ав – ас
а – (в + с) = а – в + с
(а + в) – с = а – с + в
-(а + в) = - а – в
(а-в)=а+в
а-(в+с)= а-в-с
Слайд 1510х(5х+4)=5х–4
5х –7 = 28х–3- х–4–22х
(х-5)(х+2)= (х+4)(х–7)+18
–(2х – 3)+ (х2 +2х –3)= х2
11х – 3= 2х +12 + 9х–15
–4(3у – 1)+1 =–6(2у – 1) –1
Докажите тождество
Слайд 16Выписать левую часть равенства, ее преобразовать и убедиться, что она равна
правой.
Выписать правую часть равенства, ее преобразовать и убедиться, что она равна левой.
Преобразовать и левую и правую часть равенства и убедиться в том, что они равны одному и тому же выражению.
Выписать правую часть равенства, ее преобразовать и убедиться, что она равна левой.
Преобразовать и левую и правую часть равенства и убедиться в том, что они равны одному и тому же выражению.
Слайд 18Равенства всякие, братцы, бывают, И каждый об этом, конечно же, знает. Есть –
с переменными, есть – …,
Сложные очень и очень … ,
Но есть среди равенств особенный класс,
О нем поведем свой рассказ мы сейчас.
… равенство это зовется.
Но это еще доказать нам придется.
Для этого нужно нам только лишь взять
И равенство это …
Несложно, конечно, нам будет узнать
Какую придется нам часть изменять,
А, может, придется нам обе менять,
По равенства виду нетрудно …
Ура! Удалось применить наши знания,
Окончено равенства преобразование.
И смело уже говорим мы ответ:
Так тождество это, или все-таки нет!
