- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре для подготовки к ОГЭ Теория вероятности
Содержание
- 1. Презентация по алгебре для подготовки к ОГЭ Теория вероятности
- 2. Задача 11. На экзамене 60 билетов, Олег не выучил 12
- 3. Задача 22. Средний рост жителя города, в котором
- 4. Задача 2 Средний рост жителя города, в котором
- 5. Задача 3У бабушки 25 чашек: 15 с
- 6. Задача 4На экзамене по геометрии школьнику достаётся
- 7. Задача 5
- 8. Задача 6Родительский комитет закупил 20 пазлов для
- 9. Задача 7 Фирма «Вспышка» изготавливает фонарики. Вероятность того,
- 10. Задача 8В среднем из каждых 80 поступивших
- 11. Задача 9Для экзамена подготовили билеты с номерами
- 12. Задача 10Стрелок 4 раза стреляет по мишеням.
- 13. Задача 11В таблице представлены результаты четырёх стрелков,
- 14. Задача 11Решение.Найдем относительную частоту попаданий каждого из
- 15. Задача 12 Перед началом футбольного матча
- 16. Решение.Рассмотрим все возможные исходы жеребьёвки. Команда А в матче в
- 17. Проверь себя, решив самостоятельно Задача 11) На
- 18. Задача 2Определите вероятность того, что при бросании
- 19. Задача 3Игральную кость бросают дважды. Найдите вероятность
- 20. Задача 4Саша, Семён, Зоя и Лера бросили
- 21. Задача 5В лыжных гонках участвуют 13 спортсменов
- 22. Задача 6В мешке содержатся жетоны с номерами
- 23. Задача 7В случайном эксперименте симметричную монету бросают
- 24. Задача 8В среднем из 100 карманных фонариков,
- 25. Вариант № 11. В денежно-вещевой лотерее на 100000
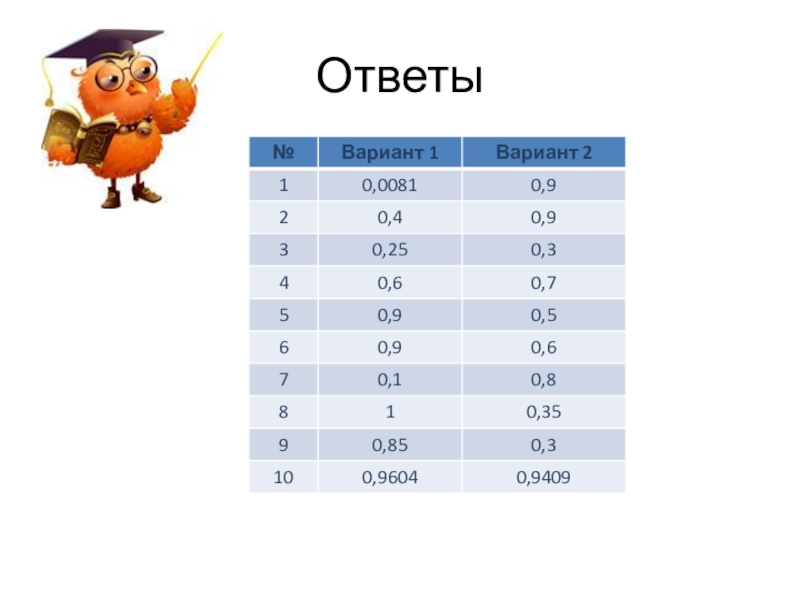
- 26. Ответы
- 27. ЛитератураОбразовательный портал для подготовки к экзаменам РЕШУ ОГЭ https://math-oge.sdamgia.ru/
Слайд 2Задача 1
1. На экзамене 60 билетов, Олег не выучил 12 из них. Найдите вероятность
Решение:
Олег выучил 60 − 12 = 48 билетов.
Таким образом вероятность
того, что ему попадётся выученный билет равна 48/60=0,8
Слайд 3Задача 2
2. Средний рост жителя города, в котором живет Никита, равен 169
1. Обязательно найдется житель с ростом менее 170 см.
2. Все жители города, кроме Никиты, имеют рост меньше 169 см.
3. Все жители города ниже Никиты.
4. Обязательно найдется житель
города с ростом 158 см.
Слайд 4Задача 2
Средний рост жителя города, в котором живет Никита, равен 169
1. Обязательно найдется житель с ростом менее 170 см. +
2. Все жители города, кроме Никиты, имеют рост меньше 169 см. -
3. Все жители города ниже Никиты. -
4. Обязательно найдется житель
города с ростом 158 см. -
Решение.
Слайд 5Задача 3
У бабушки 25 чашек: 15 с красными цветами, остальные с
Решение. Вероятность того, что чай нальют в чашку с синими цветами равна отношению количества чашек с синими цветами к общему количеству чашек. Всего чашек с синими цветами: 10/25=40/100=0,4
Слайд 6Задача 4
На экзамене по геометрии школьнику достаётся одна задача из сборника.
Решение. Суммарная вероятность несовместных событий равна сумме вероятностей этих событий: P=0,45 + 0,45 = 0,9.
Слайд 7Задача 5
Игральную кость бросают
Найдите вероятность того, что наименьшее из двух выпавших чисел равно 2.
Решение. При бросании кубика дважды равновозможны 6 · 6 = 36 различных исходов. На первом кубике должно выпасть 2 очка, а на втором — любое число кроме 1, либо наоборот, на втором кубике должно выпасть 2, а на первом — любое число кроме 1. Вероятность того, что наименьшее из двух выпавших чисел — 2 равна
9/36=1/4=0,25
Слайд 8Задача 6
Родительский комитет закупил 20 пазлов для подарков детям на окончание
Решение. Вероятность того, что Коле достанется пазл с машиной равна 10/20=1/2=0,5
Слайд 9Задача 7
Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик
Решение.
Вероятность того, что один случайно выбранный из партии фонарик — не бракованный, составляет 1 − 0,03=0,97. Вероятность того, что мы выберем одновременно два не бракованных фонарика равна 0,97 · 0,97 = 0,9409.
Слайд 10Задача 8
В среднем из каждых 80 поступивших в продажу аккумуляторов 76
Решение.
80-76=4 аккумуляторов не заряженных. Вероятность купить не заряженный аккумулятор равна отношению количества незаряженных аккумуляторов к общему числу аккумуляторов. 4/80=1/20=5/100=0,05
Слайд 11Задача 9
Для экзамена подготовили билеты с номерами от 1 до 50.
Решение.
Из 50 билетов 9 имеют однозначный номер. Вероятность, что взятый билет имеет однозначный номер равна 9/50=18/100=0,18
Слайд 12Задача 10
Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень
Решение.
Вероятность промаха равна 1 − 0,5 = 0,5. Вероятность того, что стрелок первые три раза попал в мишени равна 0,53 = 0,125. Откуда, вероятность события, при котором стрелок сначала три раза попадает в мишени, а четвёртый раз промахивается равна 0,125 · 0,5 = 0,0625.
.
Слайд 13Задача 11
В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
Тренер
.
Слайд 14Задача 11
Решение.
Найдем относительную частоту попаданий каждого из стрелков
Приведем дроби к общему
Наибольшая относительная частота попаданий у четвёртого стрелка.
Слайд 15Задача 12
Перед началом футбольного матча судья бросает монетку, чтобы
Слайд 16Решение.
Рассмотрим все возможные исходы жеребьёвки.
Команда А в матче в обоих матчах первой владеет
Команда А в матче в обоих матчах не владеет мячом первой.
Команда А в матче с командой В владеет мячом первой, а в матче с командой С — второй.
Команда А в матче с командой С владеет мячом первой, а в матче с командой В — второй.
Из четырех исходов один является благоприятным, вероятность его наступления равна 0,25.
Слайд 17Проверь себя,
решив самостоятельно
Задача 1
1) На экзамене по геометрии школьнику достаётся одна
0,9
Слайд 18Задача 2
Определите вероятность того, что при бросании игрального кубика (правильной кости)
0,5
Слайд 19Задача 3
Игральную кость бросают дважды. Найдите вероятность того, что сумма двух
0,25
Слайд 20Задача 4
Саша, Семён, Зоя и Лера бросили жребий — кому начинать
0,75
Слайд 21Задача 5
В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена
0,35
Слайд 22Задача 6
В мешке содержатся жетоны с номерами от 5 до 54
Решение.
Всего в мешке 50 жетонов. Среди них двузначное число содержат - 45.
Вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число равна 45/50=90/100=0,9
Слайд 23Задача 7
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того,
Решение.
Всего возможны четыре исхода: решка-решка, решка-орёл, орёл-решка, орёл-орёл. Орёл выпадает ровно один раз в двух случаях, поэтому вероятность того, что орёл выпадет ровно один раз равна 2/4=1/2=0,5
Слайд 24Задача 8
В среднем из 100 карманных фонариков, поступивших в продажу, восемь
Решение.
Из 100 фонариков 100 − 8 = 92 исправны. Значит, вероятность того, что выбранный наудачу в магазине фонарик окажется одним из них равна 92/100=0,92
Слайд 25Вариант № 1
1. В денежно-вещевой лотерее на 100000 билетов разыгрывается 1250 вещевых
2. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Трапеция», равна 0,1. Вероятность того, что это окажется задача по теме «Площадь», равна 0,3. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
3. У бабушки 20 чашек: 15 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
4. На экзамене по биологии школьнику достаётся один случайно выбранный вопрос из списка. Вероятность того, что этот вопрос на тему «Членистоногие», равна 0,15. Вероятность того, что это окажется вопрос на тему «Ботаника», равна 0,45. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что школьнику достанется вопрос по одной из этих двух тем.
5. На экзамене 40 билетов, Яша не выучил 4 из них. Найдите вероятность того, что ему попадется выученный билет.
6. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Площадь», равна 0,45. Вероятность того, что это окажется задача по теме «Углы», равна 0,45. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
7. В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмен из Швеции и 2 спортсмена из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что спортсмен из Швеции будет стартовать последним.
8. Средний рост жителя города, в котором живет Никита, равен 169 см. Рост Никиты 183 см. Какое из следующих утверждений верно?
1. Обязательно найдется житель с ростом менее 170 см.
2. Все жители города, кроме Никиты, имеют рост меньше 169 см.
3. Все жители города ниже Никиты.
4. Обязательно найдется житель города с ростом 158 см.
9. На экзамене 20 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный билет.
10. Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся не бракованными?
Вариант № 2
1. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Площадь», равна 0,45. Вероятность того, что это окажется задача по теме «Углы», равна 0,45. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
2. На экзамене 40 билетов, Яша не выучил 4 из них. Найдите вероятность того, что ему попадется выученный билет.
3. У бабушки 10 чашек: 7 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
4. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
5. Определите вероятность того, что при бросании игрального кубика выпадет менее 4 очков.
6. На экзамене по биологии школьнику достаётся один случайно выбранный вопрос из списка. Вероятность того, что этот вопрос на тему «Членистоногие», равна 0,15. Вероятность того, что это окажется вопрос на тему «Ботаника», равна 0,45. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
7. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что жребий начинать игру Кате не выпадет.
8. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
9. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Параллелограмм», равна 0,2. Вероятность того, что это окажется задача по теме «Площадь», равна 0,1. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
10. Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,03. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся не бракованными?