- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре для 9 класса Основные понятия. Уравнения с двумя переменными и их системы.
Содержание
Является ли пара чисел ( ) решением уравнения 2х2 – у2 = 1 ?
Слайд 3(x – 7 )2 + (y + 4)2 = 16
x2 +
(y – 9)2 = 100
(x + 5 )2 + y2 = 7
x2 + y 2 = 13
r
C(7; -4)
C(0;9)
C(-5; 0)
C(0; 0)
r = 4
r = 10
Слайд 5Система уравнений и её решение
Определения
Системой уравнений называется некоторое
количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно
Решить систему уравнений - это значит найти все её решения или установить, что их нет
Решить систему уравнений - это значит найти все её решения или установить, что их нет
Слайд 6Решение системы уравнений с двумя переменными
Определение
Решением системы
уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
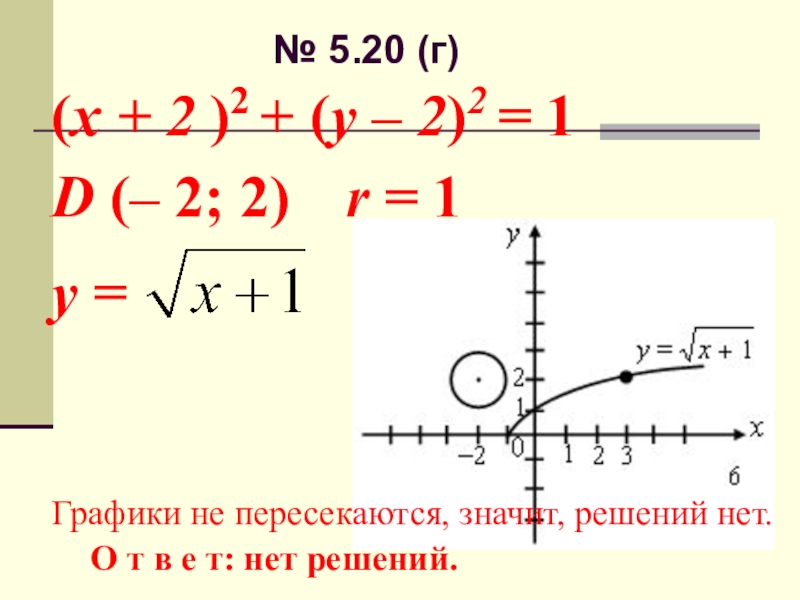
Слайд 7№ 5.20 (г)
(x + 2 )2 + (y – 2)2 =
1
D (– 2; 2)
r = 1
у =
Графики не пересекаются, значит, решений нет.
О т в е т: нет решений.