- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре а тему Ньютон
Содержание
- 1. Презентация по алгебре а тему Ньютон
- 2. Тема урока: Применение определённого интеграла в решении геометрических и физических задач.
- 3. Фронтальный опрос:
- 4. 1.Что такое первообразная?
- 5. Если для любого х
- 6. 2.Что такое неопределённый интеграл?
- 7. Совокупность всех первообразных функции F(x)+С
- 8. 3.Что такое определённый интеграл?
- 9. Число , к которому
- 10. 4. Дайте определение криволинейной трапеции.
- 11. Фигуру, ограниченную графиком непрерывной
- 12. 5. В чём заключается геометрический и физический смысл интеграла?
- 13. Интеграл применяют в решении геометрических и физических задач:
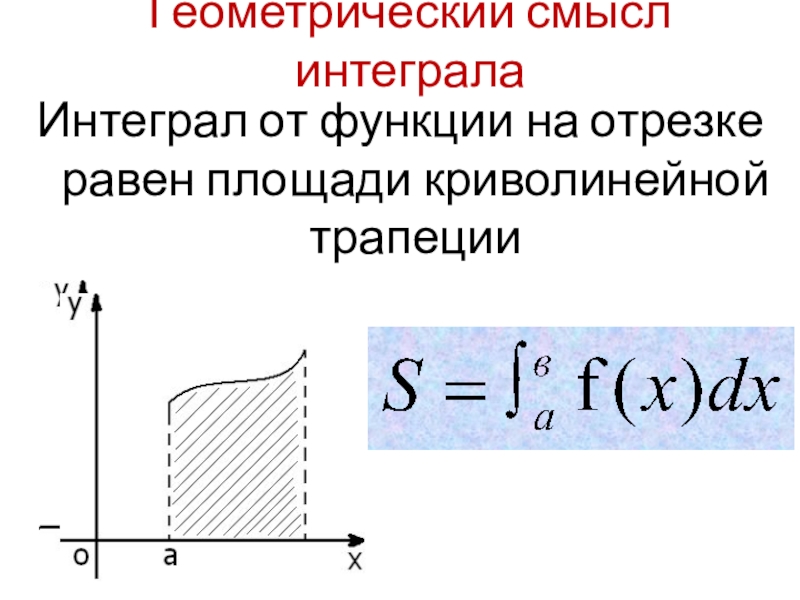
- 14. Геометрический смысл интегралаИнтеграл от функции на отрезке равен площади криволинейной трапеции
- 15. Физический смысл интеграла
- 16. Слайд 16
- 17. 6. Назовите формулу Ньютона-Лейбница.
- 18. Формула Ньютона-Лейбница
- 19. Назовите общий вид первообразных элементарных функций.
- 20. f(x) = k
- 21. Разминка : Самостоятельная
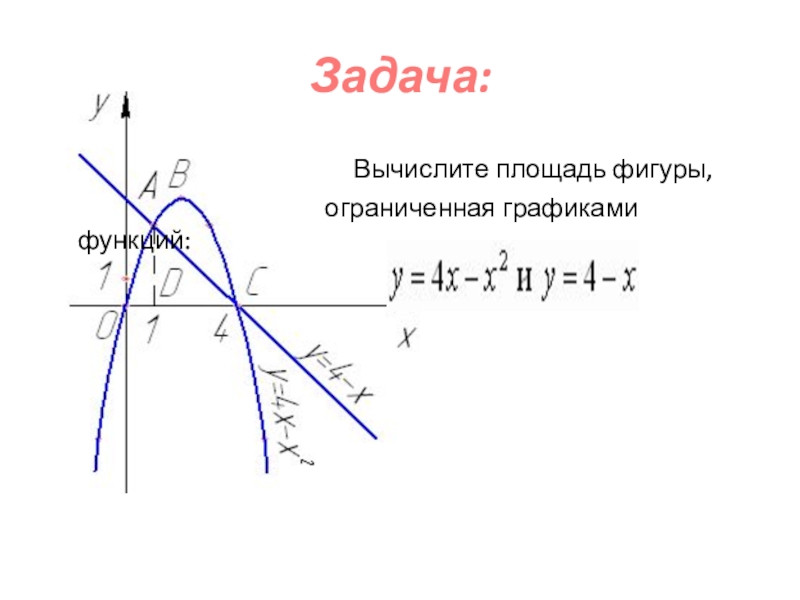
- 22. Задача:
- 23. Ключ к тесту «А»:
- 24. Блиц – турнир: Найдите и исправьте ошибки:
- 25. 1 234567
- 26. Задача: Материальная точка движется по
- 27. Ответ:1/4 (м) или 25 (см).
- 28. История возникновения метода интегрирования.
- 29. Ньютон (XVII в)
- 30. Слайд 30
- 31. Бернулли(XVIII)
- 32. Вычисление объемов тел с помощью определенного интеграла
- 33. Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом.
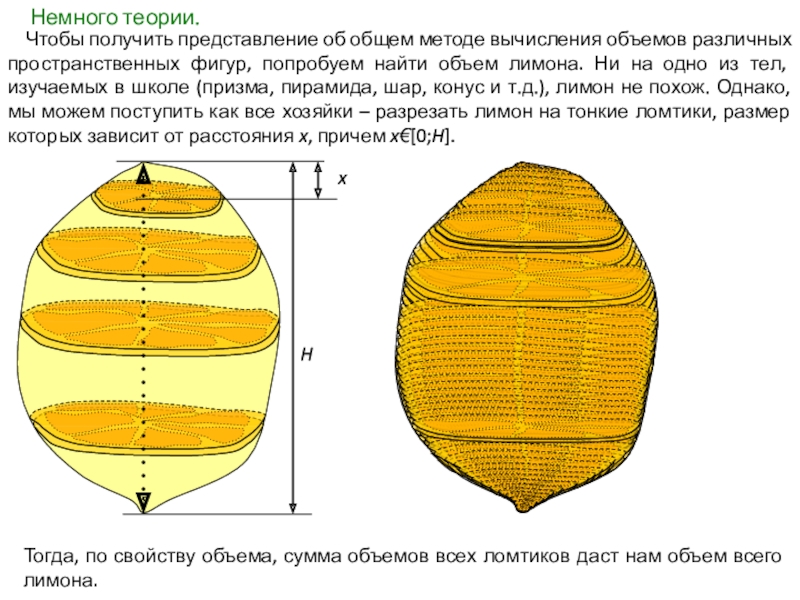
- 34. Немного теории. Чтобы получить представление об
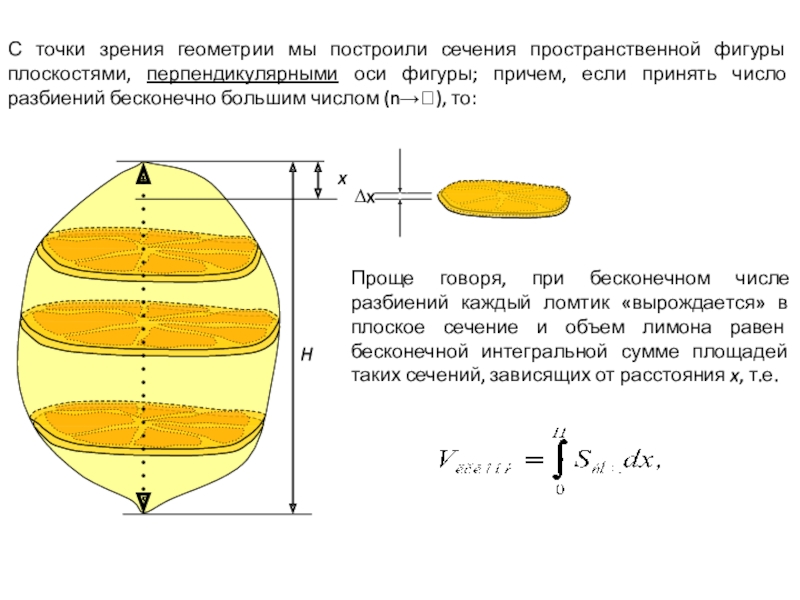
- 35. Hx∆∆x∆xxС точки зрения геометрии мы построили сечения
- 36. Укажем общий способ
- 37. На промежутке (a; b)
- 38. Объем V (x) является первообразной для функции S (x) (площади сечения) на промежутке [a; b]. Отсюда имеем:
- 39. АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЪЁМОВ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ПОМОЩЬЮ
- 40. Объем конуса с высотой H и площадью
- 41. Объем цилиндра с высотой H и площадью
- 42. Объем шара с радиусом R.Найдем объем
- 43. Задание на дом. №53(2), № 63
- 44. Учитель Бережная И.В.Спасибо за внимание!
Слайд 5 Если для любого х из множества Х выполняется
Слайд 7 Совокупность всех первообразных функции F(x)+С для функции f(x) называется
Слайд 9 Число , к которому стремится площадь криволинейной трапеции,
Слайд 11 Фигуру, ограниченную графиком непрерывной функции у= f(x) ,
Слайд 14Геометрический смысл интеграла
Интеграл от функции на отрезке равен площади криволинейной трапеции
Слайд 15Физический смысл интеграла
Известно : a(t)=V´(t),
тогда скорость равна:
V =
S =
Известно: V(t) = S´(t),
тогда перемещение равно:
Слайд 20f(x) = k
f(x) = хn
f(x) = sinx
f(x) = cosx
f(x) =
f(x) =
F(x) =
F(x) =
F(x) =
F(x) =
F(x) =
F(x) =
kх+С
-cos x+С
sin x+С
-ctg x+С
tg x+С
+С
Слайд 21Разминка :
Самостоятельная работа с тестом по учебнику:
Раздел «В» (стр.33 вопросы 5,6,7)
Раздел «С» (стр.33 вопросы 8,9,10)
Слайд 23Ключ к тесту «А»:
Ключ к тесту «В»:
5. С, 6. С, 7. Д.
Ключ к тесту «С»:
8. В, 9. Д, 10. С.
Слайд 26 Задача: Материальная точка движется по прямой со скоростью V(t)=sint·cost
Слайд 33
Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую
Слайд 34Немного теории.
Чтобы получить представление об общем методе вычисления объемов
H
x
Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего лимона.
Слайд 35H
x
∆∆x∆xx
С точки зрения геометрии мы построили сечения пространственной фигуры плоскостями, перпендикулярными
Проще говоря, при бесконечном числе разбиений каждый ломтик «вырождается» в плоское сечение и объем лимона равен бесконечной интегральной сумме площадей таких сечений, зависящих от расстояния x, т.е.
∆x
Слайд 36
Укажем общий способ вычисления объемов тел
Пусть криволинейная трапеция, то есть фигура, ограниченная осью Ox, прямыми x = a, x = b и графиком непрерывной возрастающей неотрицательной функции y = f (x), вращается вокруг оси Ox (рис.1), вследствие чего образуется тело вращения. Сечение этого тела плоскостью, перпендикулярной оси Ox, есть круг или точка.
Рис.1
Слайд 37
На промежутке (a; b) выберем точку x.
Слайд 38Объем V (x) является первообразной для функции S (x) (площади сечения) на промежутке
Слайд 39АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЪЁМОВ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА.
1. Ввести систему
2. Найти пределы интегрирования а и b.
3. Провести сечение плоскостью перпендикулярно оси ОХ через точку с абсциссой х.
Определить вид сечения, задать формулой его площадь как функцию S(X).
4. Проверить непрерывность функции S(X) на [a;b].
5. Составить интеграл и вычислить его по формуле:
Слайд 40Объем конуса с высотой H и площадью основания S.
x
х€[0;H]
H
x
Площадь сечения изменяется
0
Слайд 41Объем цилиндра с высотой H и площадью основания S.
x
x€[0;H]
H
0
x
Площадь сечения не
Слайд 42 Объем шара с радиусом R.
Найдем объем полушария, как бесконечную интегральную
R
x
Значит, объем всего шара равен:
x
0
r








![Презентация по алгебре а тему Ньютон Число , к которому стремится площадь криволинейной трапеции, построенной Число , к которому стремится площадь криволинейной трапеции, построенной на отрезке [a;b] , называют](/img/thumbs/9d2e9ddceaa1c97662db019fa9681eb2-800x.jpg)







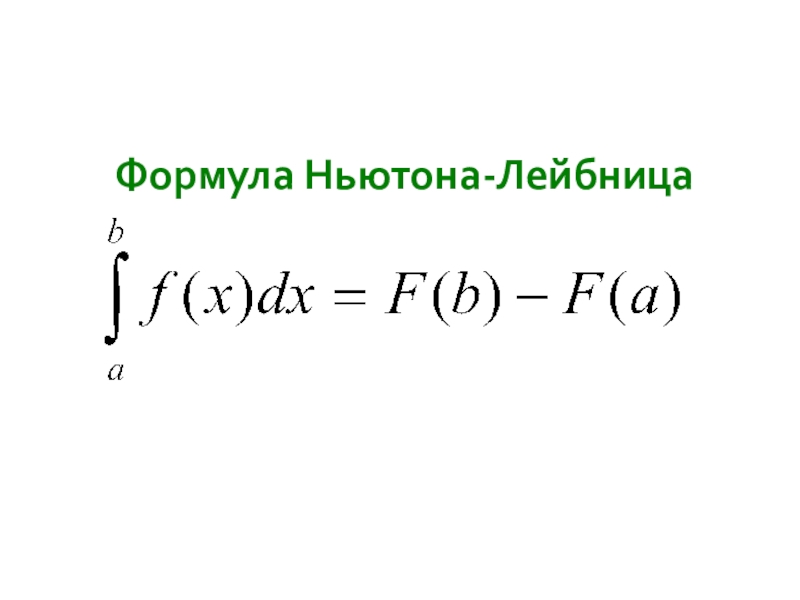

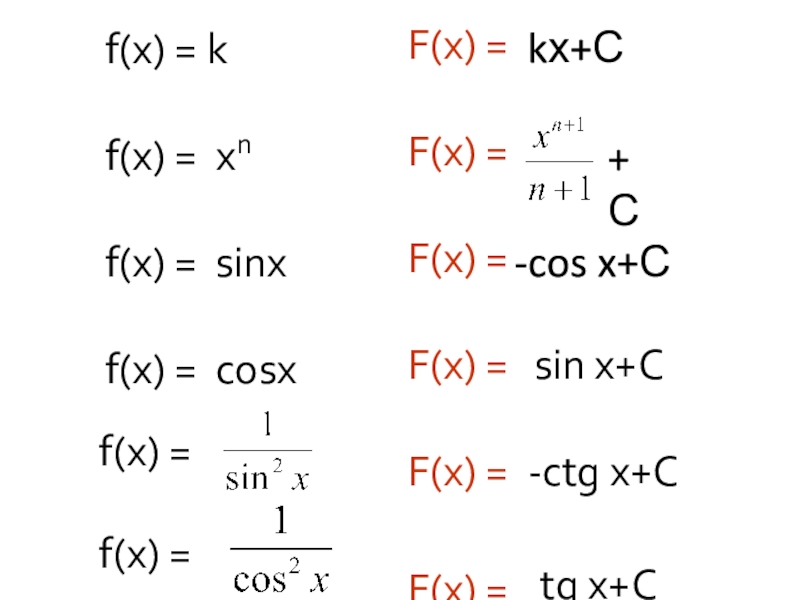



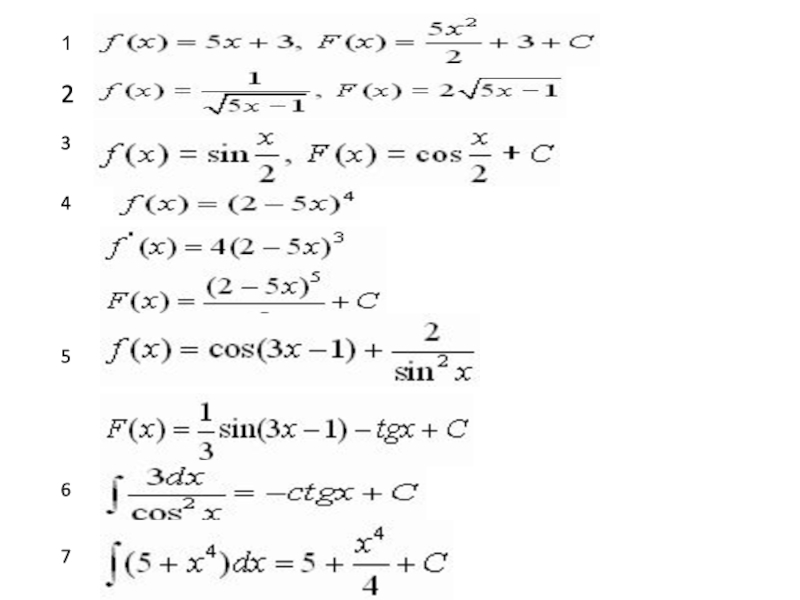










![Презентация по алгебре а тему Ньютон Объем V (x) является первообразной для функции S (x) (площади сечения) на промежутке [a; b]. Отсюда имеем: Объем V (x) является первообразной для функции S (x) (площади сечения) на промежутке [a; b]. Отсюда имеем:](/img/thumbs/47cc2b97d3a08315124d34949dbbb6c4-800x.jpg)

![Презентация по алгебре а тему Ньютон Объем конуса с высотой H и площадью основания S.xх€[0;H]HxПлощадь сечения изменяется Объем конуса с высотой H и площадью основания S.xх€[0;H]HxПлощадь сечения изменяется в зависимости от расстояния x, причем](/img/thumbs/c7c37097935d2a9dbc35e4e8cbb269cd-800x.jpg)
![Презентация по алгебре а тему Ньютон Объем цилиндра с высотой H и площадью основания S.xx€[0;H]H0xПлощадь сечения не Объем цилиндра с высотой H и площадью основания S.xx€[0;H]H0xПлощадь сечения не изменяется в любой точке отрезка от](/img/thumbs/9001d05be5456c2ee03f143a3b2d13a9-800x.jpg)








