- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре 9 класс на тему Арифметическая прогрессия
Содержание
- 1. Презентация по алгебре 9 класс на тему Арифметическая прогрессия
- 2. Цель урока:закрепить умения и навыки применения формул
- 3. Арифметическая прогрессия
- 4. Выписаны первые несколько членов арифметической прогрессии: -8; 1; 6; ... Найдите 7-й член этой прогрессии.
- 5. Выписаны первые несколько членов арифметической прогрессии: -7;
- 6. Выписано несколько последовательных членов арифметической прогрессии: ...;
- 7. Является ли число 35,8 членом арифметической прогрессии
- 8. Самостоятельная работа
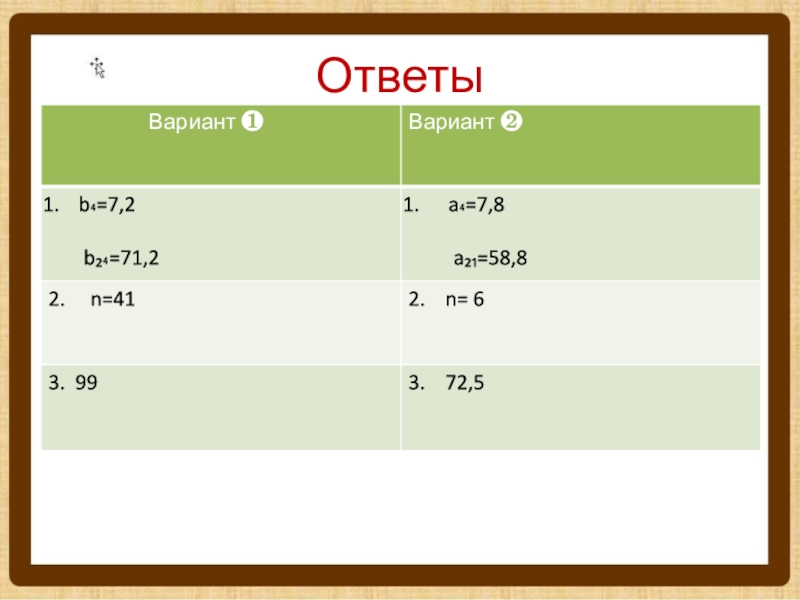
- 9. Ответы
Слайд 2Цель урока:
закрепить умения и навыки применения формул n-го члена и свойства
-закреплять умения и навыки применения формулы суммы первых n членов арифметической прогрессии при решении задач; провести подготовку к контрольной работе.
Слайд 4Выписаны первые несколько членов арифметической прогрессии: -8; 1; 6; ... Найдите
Слайд 5Выписаны первые несколько членов арифметической прогрессии: -7; -4; -1; ... Найдите
найдем разность d арифметической прогрессии по формуле
найдем шестой член арифметической прогрессии по формуле при n=6, получим:
Сумму первых шести членов находим по формуле:
Ответ: 3
Слайд 6Выписано несколько последовательных членов арифметической прогрессии: ...; -9; x; -13; -15;
Найдем величину из двух соседних членов прогрессии -13 и -15, получим:
Ответ: -11
Слайд 7Является ли число 35,8 членом арифметической прогрессии (ап), в которой а1
(ап) – арифметическая прогрессия; а1 = 11,6; а15 = 17,2.
Пусть ап = 30,4.
d = ; d = = = 0,4;
ап = а1 + d (n – 1); 30,4 = 11,6 + 0,4 (n – 1); 0,4 (n – 1) = 18,8;
n – 1 = 47; n = 48, n принадлежит N, значит, 30,4 является членом арифметической прогрессии (аn).
О т в е т: да.
Слайд 8Самостоятельная работа
1 В арифметической прогрессии (bп) известны b1 = –0,8, d = 4. Найдите b3; b24.
2 В арифметической прогрессии (хп) известны х1 = 14 и d = 0,5. Найдите номер члена прогрессии, равного 34.
3 Найдите сумму первых двенадцати членов арифметической прогрессии, если а1 = 16,5; d = –1,5.
Вариант ❷
1 В арифметической прогрессии (ап) известны а1 = –1,2, d = 3. Найдите а4; а21.
2 В арифметической прогрессии (bп) известны b1 = 12 и d = 3. Найдите номер члена прогрессии, равного 27.
3 Найдите сумму первых десяти членов арифметической прогрессии, если а1 = 18,5; d = –2,5.