Тема:
Некоторые редкие формулы тригонометрии: формулы Моллвейде, теоремы тангенсов и котангенсов.
Подготовил: ученик 9 г класса
Цапенко О.С.
Руководитель:Мощенко О.В
г. Хабаровск
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад некоторые редкие формулы тригонометрии
Содержание
- 1. Презентация некоторые редкие формулы тригонометрии
- 2. Йоганн МюллерОсновным математическим трудом Региомонтана было сочинение
- 3. Теорема тангенсов
- 4. Доказательство:
- 5. согласно известному тригонометрическому тождеству- суммы и разности синусов двух угловполучаем
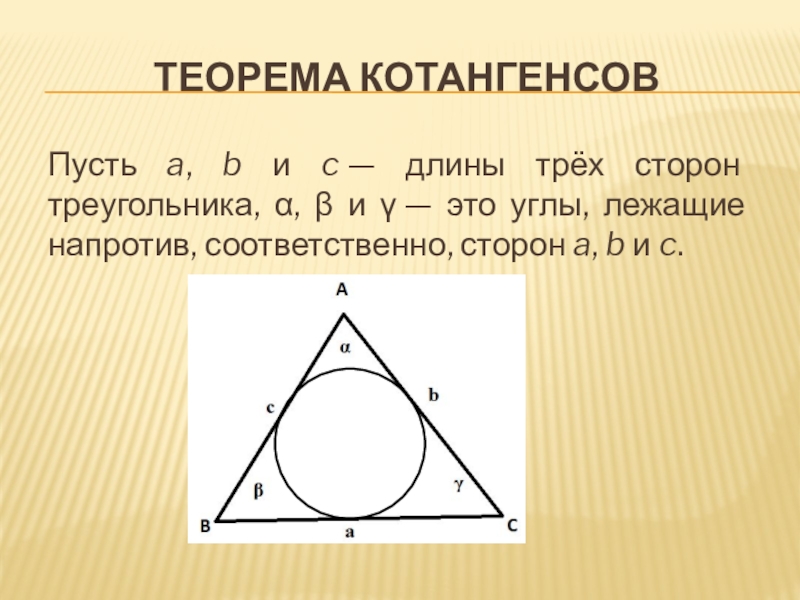
- 6. Теорема котангенсовПусть a, b и c — длины
- 7. Теорема котангенсов утверждает, что еслиr (радиус вписанной
- 8. Следовательно: котангенс
- 9. Формулы МоллвейдеКарл Моллвейде Годы жизни: 1774-1825Именем Моллвейде
- 10. Слайд 10
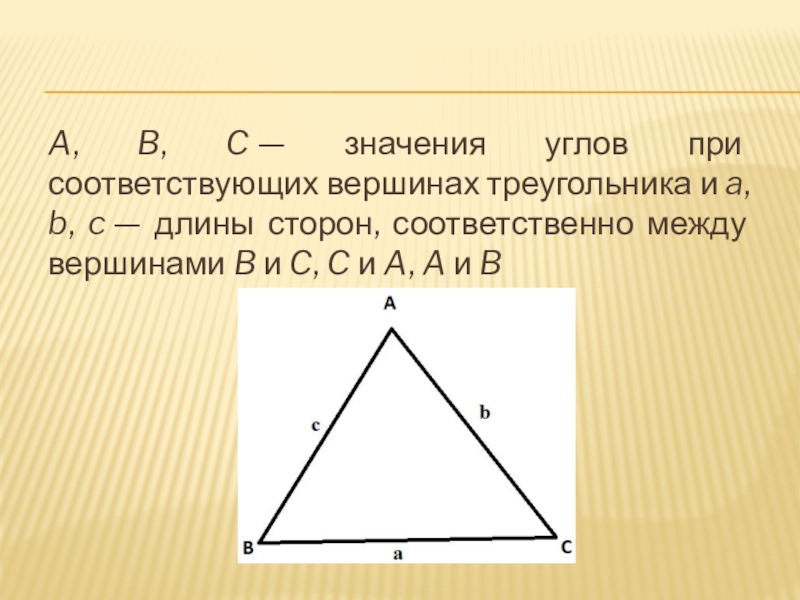
- 11. A, B, C — значения углов при соответствующих
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Благодарю за внимание!
Йоганн МюллерОсновным математическим трудом Региомонтана было сочинение «О всех видах треугольников» (1462—1464). Это был первый труд в Европе, в котором тригонометрия рассматривалась как самостоятельная дисциплина.Годы жизни:1436-1476
Слайд 1
МБОУСОШ № 11
Слайд 2Йоганн Мюллер
Основным математическим трудом Региомонтана было сочинение «О всех видах треугольников»
(1462—1464). Это был первый труд в Европе, в котором тригонометрия рассматривалась как самостоятельная дисциплина.
Годы жизни:1436-1476
Слайд 5
согласно известному тригонометрическому тождеству- суммы и разности синусов двух углов
получаем
Слайд 6Теорема котангенсов
Пусть a, b и c — длины трёх сторон треугольника, α,
β и γ — это углы, лежащие напротив, соответственно, сторон a, b и c.
Слайд 7Теорема котангенсов утверждает, что если
r (радиус вписанной окружности треугольника) и
p (полупериметр
треугольника),
то справедливы следующие формулы:
; ;
то справедливы следующие формулы:
; ;
Слайд 8
Следовательно: котангенс половинного угла равен отношению полупериметра минус длина противолежащей стороны
указанного угла к радиусу вписанной окружности.
Слайд 9Формулы Моллвейде
Карл Моллвейде
Годы жизни: 1774-1825
Именем Моллвейде названы картографическая проекция Моллвейде—
равновеликая эллиптическая псевдоцилиндрическая проекция, а также тригонометрические формулы, выражающие зависимость между длинами сторон и углами треугольника.
Слайд 11A, B, C — значения углов при соответствующих вершинах треугольника и a,
b, c — длины сторон, соответственно между вершинами B и C, C и A, A и B
Слайд 12
Доказательство:
согласно тому, что a=2R sinA; b=2R sinB; c=2R sinC
отсюда
преобразуем вторую часть согласно тригонометрическому тождеству- суммы и разности синусов двух углов,
а так как
,то