Выполнила учитель
МКОУ Коченевская СОШ № 13
С.В. Скидан
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Модуль действительного числа.
Содержание
- 1. Презентация Модуль действительного числа.
- 2. определение модуля Геометрическая интерпретация определения.
- 3. Свойства модулей
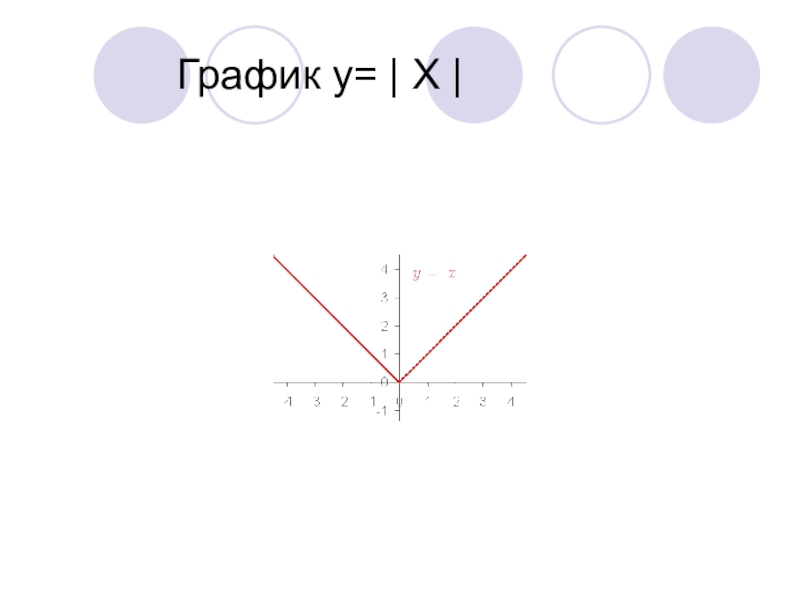
- 4. График у= | Х |
- 5. Вычисления выражений, содержащих модуль свойство модуля
- 6. Вычислите
- 7. Примеры решения уравнений, содержащих абсолютные величины.
- 8. Уравнение вида │f(х)│= g(х) Уравнение вида │f(х)│=
- 9. Уравнение вида │f(x)│=│g(x)│ Уравнение вида │f(x)│=│g(x)│ равносильно
- 10. выводы
- 11. Метод интервалов в решении уравнений, содержащих модуль.
- 12. Пример: 2│х-2│-3│х+4│=1.Решение.1). Найдём
определение модуля Геометрическая интерпретация определения. -а о а
Слайд 5 Вычисления выражений, содержащих модуль
свойство модуля
и его
значение для упрощения выражений
Пример:
Пример:
так как
Значит
Слайд 7Примеры решения уравнений, содержащих абсолютные
величины.
Уравнения вида │х│=а, если а
решений не имеют; если а=о, то х=о; если же а>о, то х=а и х=-а.
Пример: │х│= 7 по определению модуля данное уравнение имеет корни х=7, х=-7.
Уравнение вида f(│х│) = а, где а≥о равносильно объединению уравнений:
f(х)=а
f(х)=-а.
Пример: │2х-3│ = 2 по определению абсолютной величины имеем: 2х-3=2, х=2,5,
=>
2х-3=-2; х=0,5.
Ответ: х1=2,5; х2=0,5.
Пример: │х│= 7 по определению модуля данное уравнение имеет корни х=7, х=-7.
Уравнение вида f(│х│) = а, где а≥о равносильно объединению уравнений:
f(х)=а
f(х)=-а.
Пример: │2х-3│ = 2 по определению абсолютной величины имеем: 2х-3=2, х=2,5,
=>
2х-3=-2; х=0,5.
Ответ: х1=2,5; х2=0,5.
Слайд 8Уравнение вида │f(х)│= g(х)
Уравнение вида │f(х)│= g(х) равносильно системе уравнений:
f(х)= g(х),
f(х)= - g(х)
g(х)≥0.
Пример: │2х-5│= х-1
Решение:Уравнение вида │f(х)│= g(х)
2х-5=х-1, х=4,
2х-5=1-х, х=2, => х1=4; х2=2;
х-1≥0. х≥1.
Ответ: х1=4, х2=2.
f(х)= - g(х)
g(х)≥0.
Пример: │2х-5│= х-1
Решение:Уравнение вида │f(х)│= g(х)
2х-5=х-1, х=4,
2х-5=1-х, х=2, => х1=4; х2=2;
х-1≥0. х≥1.
Ответ: х1=4, х2=2.
Слайд 9Уравнение вида │f(x)│=│g(x)│
Уравнение вида │f(x)│=│g(x)│ равносильно объединению уравнений
f (x)=g(x),
f (x)=-g(x). Уравнение вида │f(x)│=│g(x)│
Пример : │2-3х│=│5-2х│Уравнение вида │f(x)│=│g(x)│
2-3х=5-2х, -х=3, х=-3,
2-3х=2х-5; -5х=-7; х=1,4.
Ответ: х1=-3, х2=1,4.
f (x)=-g(x). Уравнение вида │f(x)│=│g(x)│
Пример : │2-3х│=│5-2х│Уравнение вида │f(x)│=│g(x)│
2-3х=5-2х, -х=3, х=-3,
2-3х=2х-5; -5х=-7; х=1,4.
Ответ: х1=-3, х2=1,4.
Слайд 11Метод интервалов в решении уравнений, содержащих модуль.
Уравнения вида │f1(х)│+│f2(x)│+……+│fn(x)│=g(x) решают
так: для каждой из этих функций находят область определения, её нули и точки разрыва. Нули и точки разрыва разбивают общую область определения функции fj(x) (j=1,2,…n) на промежутки, в каждом из которых каждая из функций fj(х) сохраняет постоянный знак. Далее используя определение модуля, для каждой из найденных областей получим уравнение, подлежащее решению.
Алгоритм решения уравнения F(x)=0, где его левая часть содержит модули некоторых функций │f1(x)│, │f2(x)│, ……│fn(x)│:
Решают каждое из уравнений f1(x)=0,f2(x)=0,…fn(x)=0.
Вся координатная ось разбивается на некоторое число промежутков.
На каждом таком промежутке уравнение заменяется на другое уравнение, не содержащее знаков модуля и равносильное исходному уравнению на этом промежутке.
На каждом промежутке отыскиваются корни того уравнения, которое на этом промежутке получается.
Отбираются те корни, которые принадлежат данному промежутку. Они и будут корнями исходного уравнения на рассматриваемом промежутке.
Все корни уравнения F(x)=0 получают, объединяя все корни, найденные на всех промежутках.
Алгоритм решения уравнения F(x)=0, где его левая часть содержит модули некоторых функций │f1(x)│, │f2(x)│, ……│fn(x)│:
Решают каждое из уравнений f1(x)=0,f2(x)=0,…fn(x)=0.
Вся координатная ось разбивается на некоторое число промежутков.
На каждом таком промежутке уравнение заменяется на другое уравнение, не содержащее знаков модуля и равносильное исходному уравнению на этом промежутке.
На каждом промежутке отыскиваются корни того уравнения, которое на этом промежутке получается.
Отбираются те корни, которые принадлежат данному промежутку. Они и будут корнями исходного уравнения на рассматриваемом промежутке.
Все корни уравнения F(x)=0 получают, объединяя все корни, найденные на всех промежутках.
Слайд 12Пример:
2│х-2│-3│х+4│=1.
Решение.
1). Найдём критические точки:
а) х-2=0 б) х+4=0
х=2 х=-4
2) х-2 - -4 - 2 +
х+4 - + + х
3) 1. х<-4, 2. -4≤х≤2, 3. х>2,
-2х+4+3х+12=1, -2х+4-3х-12=1, 2х-4-3х-12=1,
x<-4, -4≤х≤2, х>2
х=-15. х=-1,8. х=-17
х = -15. х = -1,8.
Ответ: x1 = -15, х2 = -1,8.
х=2 х=-4
2) х-2 - -4 - 2 +
х+4 - + + х
3) 1. х<-4, 2. -4≤х≤2, 3. х>2,
-2х+4+3х+12=1, -2х+4-3х-12=1, 2х-4-3х-12=1,
x<-4, -4≤х≤2, х>2
х=-15. х=-1,8. х=-17
х = -15. х = -1,8.
Ответ: x1 = -15, х2 = -1,8.