- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Методическая разработка по алгебре на темуКвадратные уравнения(8 класс)
Содержание
- 1. Презентация. Методическая разработка по алгебре на темуКвадратные уравнения(8 класс)
- 2. Елушова З.Н., учитель математики высшей категории
- 3. СодержаниеПояснительная запискаСодержание обученияМетоды и формы обученияФормы контроляДидактические
- 4. Пояснительная запискаМетодическая разработка темы «Квадратные уравнения» разработана
- 5. Пояснительная запискаСодержание обучения
- 6. Дидактические целиОбразовательные:Формировать умениярешать квадратные уравнения по формуле;решать
- 7. Дидактические цели Развивающие: Развиватьлогическое и
- 8. Ожидаемые результаты освоения темыВ результате изучения темы
- 9. Учебно-тематическое планирование
- 10. Урок № 3 Тема урока. Формула корней
- 11. Структура урокаОрганизационный момент.Актуализация знаний.Введение проблемной ситуации.Ознакомление с новой темой.Первичное закрепление.Домашнее задание.Подведение итогов работы.
- 12. Ход урока.1. Организационный момент.Сообщить тему урока, сформулировать
- 13. 2. Актуализация знаний. x2 – 16 =
- 14. 6. Домашнее задание.П. 22, № 533, №
- 15. Алгоритм решения квадратного уравнения. Вычислить дискриминант квадратного
- 16. Алгоритм решения квадратного уравненияВычислить дискриминант квадратного уравнения
- 17. Результаты выполнения самостоятельных и контрольных работ по теме: «Квадратные уравнения»
- 18. Самостоятельные и контрольные работы по теме:
- 19. Самостоятельные и контрольные работы по теме:
- 20. Самостоятельная работа №1.Вариант 1.Туристы отправляются на лодке
- 21. Контрольная работа №11 вариант
- 22. Квадратные уравнениянеполные:ax2 + bx + c =
- 23. неполные:приведенные:ax2 + bx + c = 0x2 + px + q = 0полные:
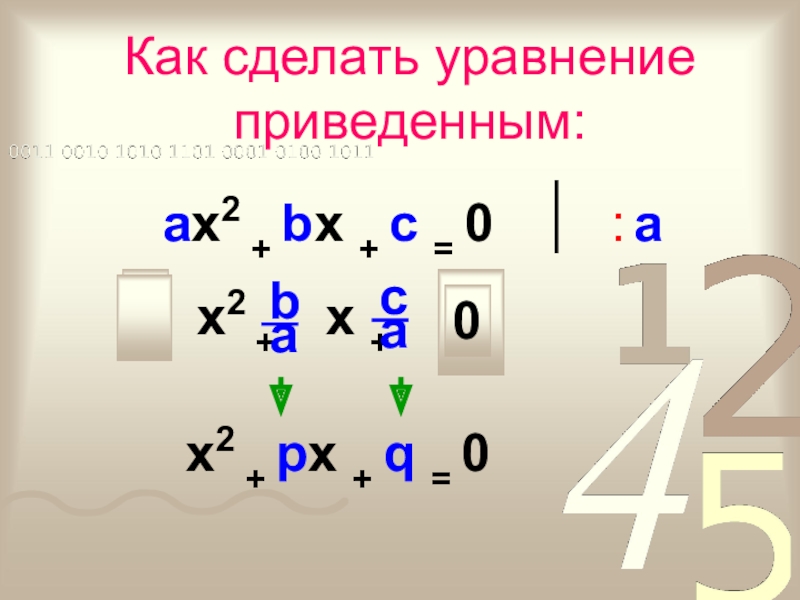
- 24. 1Как сделать уравнение приведенным:ax2 + bx +
- 25. Виета x2 + px + q = 0x1 + x2 = - pТеорема
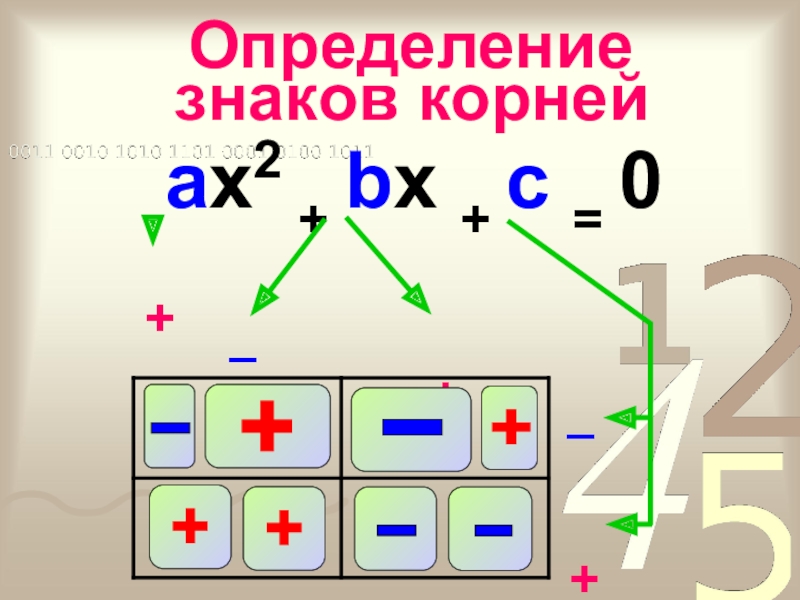
- 26. ax2 + bx + c = 0+_+_+
- 27. ЛитератураТ.А. Бурмистрова. Алгебра. Программы общеобразовательных учреждений. М.:
Слайд 2Елушова З.Н., учитель математики высшей категории
МОУ «Саваслейской средней общеобразовательной школы»
Образование:
Квалификация: учитель математики и физики.
Педагогический стаж: 36 лет.
Категория: высшая с 2001 г.
Стаж работы в МОУ «Саваслейской СОШ»: 22 г.
Методическая разработка по алгебре
Квадратные уравнения (8 класс)
Слайд 3Содержание
Пояснительная записка
Содержание обучения
Методы и формы обучения
Формы контроля
Дидактические цели
Ожидаемые результаты освоения темы
Учебно-тематическое
Урок №3
Самостоятельные и контрольные работы по теме: «Квадратные уравнения»
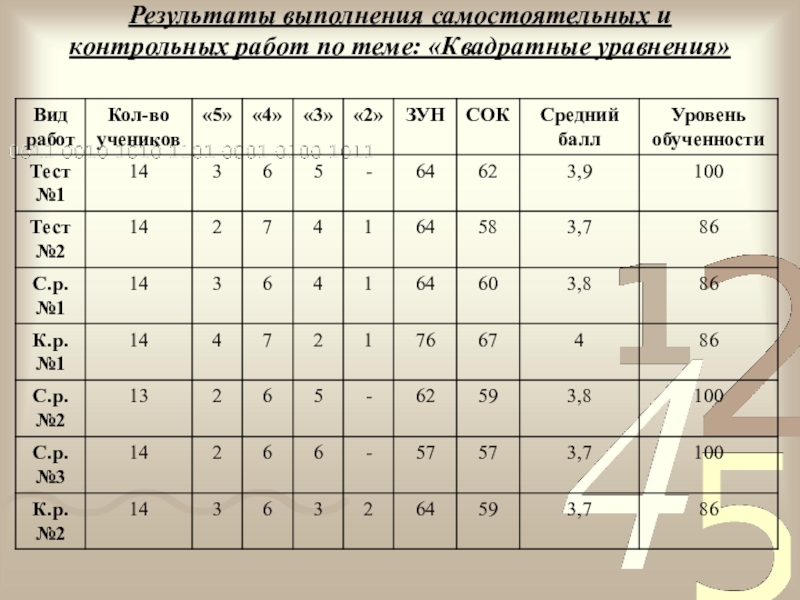
Результаты выполнения самостоятельных и контрольных работ по теме: «Квадратные уравнения»
Литература
Слайд 4Пояснительная записка
Методическая разработка темы «Квадратные уравнения» разработана на основе
Программы общеобразовательных
Преподавание ведется по учебнику:
Алгебра: Учебник для 8 класса общеобразовательных учреждений.
Под ред. Теляковского С.А. Москва: «Просвещение», 2008 г.
Слайд 5Пояснительная записка
Содержание обучения
Тема. «Квадратные
Квадратное уравнение. Формула корней квадратного уравнения.
Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Основная цель:
Выработать умения решать квадратные уравнения и простейшие рациональные и применять их к решению задач.
Методы и формы обучения:
Методы: объяснительный, проблемный, частично-поисковый,
исследовательский.
Формы: фронтальная, индивидуальная, групповая.
Формы контроля:
Тесты, самостоятельная работа, контрольная работа, зачет.
Слайд 6Дидактические цели
Образовательные:
Формировать умения
решать квадратные уравнения по формуле;
решать квадратные уравнения по теореме,
решать дробные рациональные уравнения;
решать текстовые задачи с помощью квадратных и дробных рациональных уравнений.
Формировать знания
что такое квадратное уравнение, неполное квадратное уравнение, приведенное квадратное уравнение;
какие уравнения называются дробными рациональными;
о способах решения квадратных уравнений.
Слайд 7Дидактические цели
Развивающие:
Развивать
логическое и алгоритмическое мышление;
способность к контролю
умение сравнивать, выявлять, обобщать закономерности.
Воспитательные:
Воспитывать
трудолюбие, волю, настойчивость для достижения конечных результатов;
способность к преодолению трудностей.
Слайд 8Ожидаемые результаты освоения темы
В результате изучения темы «Квадратные уравнения» ученик должен
знать (понимать):
как используются формулы корней квадратного уравнения;
примеры применения квадратных уравнений для решения математических и практических задач;
уметь:
распознавать квадратные уравнения;
решать квадратные уравнения, а также уравнения, сводящиеся к ним;
решать дробно-рациональные уравнения;
исследовать квадратные уравнения по дискриминанту и коэффициентам;
решать текстовые задачи с помощью квадратных уравнений и дробных рациональных уравнений.
использовать знания и умения в практической деятельности и повседневной жизни:
для выполнения расчетов по формулам.
Слайд 10Урок № 3 Тема урока. Формула корней квадратного уравнения. Тип урока. Урок изучения
Цели урока: найти способ решения квадратного уравнения, используя метод выделения квадрата двучлена.
В результате ученик
Знает
какая учебная задача стоит перед ним при изучении темы;
что такое дискриминант и сколько корней может иметь квадратное уравнение;
способ решения квадратного уравнения.
Умеет
находить дискриминант квадратного уравнения, отвечать на вопрос: сколько корней имеет квадратное уравнение;
решать квадратные уравнения по формуле.
Слайд 11Структура урока
Организационный момент.
Актуализация знаний.
Введение проблемной ситуации.
Ознакомление с новой темой.
Первичное закрепление.
Домашнее задание.
Подведение
Слайд 12Ход урока.
1. Организационный момент.
Сообщить тему урока, сформулировать цели урока.
2. Актуализация знаний.
В ходе фронтального опроса ученики отвечают на вопросы (слайд № 13 ).
3. Постановка проблемы:
- Как вы думаете, можно ли методом выделения полного квадрата решить квадратное уравнение общего вида?
4. Открытие нового знания.
Вместе с учениками решаем квадратное уравнение общего вида выделением полного квадрата. Составляем алгоритм решения квадратного уравнения и схему решения квадратного уравнения.
5. Первичное закрепление.
учащиеся решают уравнения (первое уравнение – учитель)
фронтальная работа № 535
работа в парах № 534 (по очереди объясняют решение друг другу)
Самостоятельная работа (обучающая № 540)
6. Домашнее задание.
7. Подведение итогов.
Слайд 132. Актуализация знаний.
x2 – 16 = 0;
x2 + 9
3x – 10 + x2 = 0;
3x2 – 12x = 0;
3x2 – 7x + 2 = 0;
2x2 + 5x – 3 = 0
Какие уравнения записаны на доске?
Докажите, что данные уравнения квадратные.
Назовите приведенные квадратные уравнения.
Как решить первое и четвертое уравнения?
Слайд 146. Домашнее задание.
П. 22,
№ 533,
№ 541,
№545.
7. Подведение итогов.
Сколько
От чего зависит наличие корней квадратного уравнения?
Назовите формулу корней квадратного уравнения.
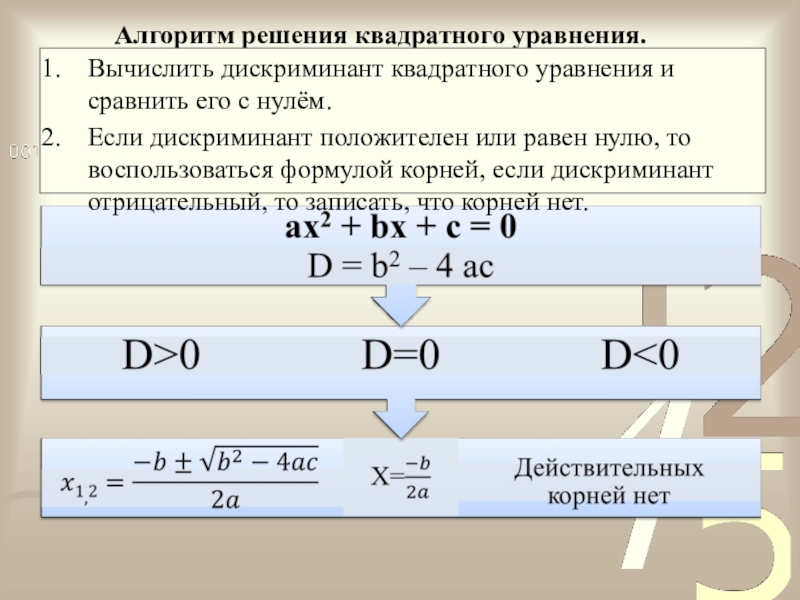
Слайд 15Алгоритм решения квадратного уравнения.
Вычислить дискриминант квадратного уравнения и сравнить его с
Если дискриминант положителен или равен нулю, то воспользоваться формулой корней, если дискриминант отрицательный, то записать, что корней нет.
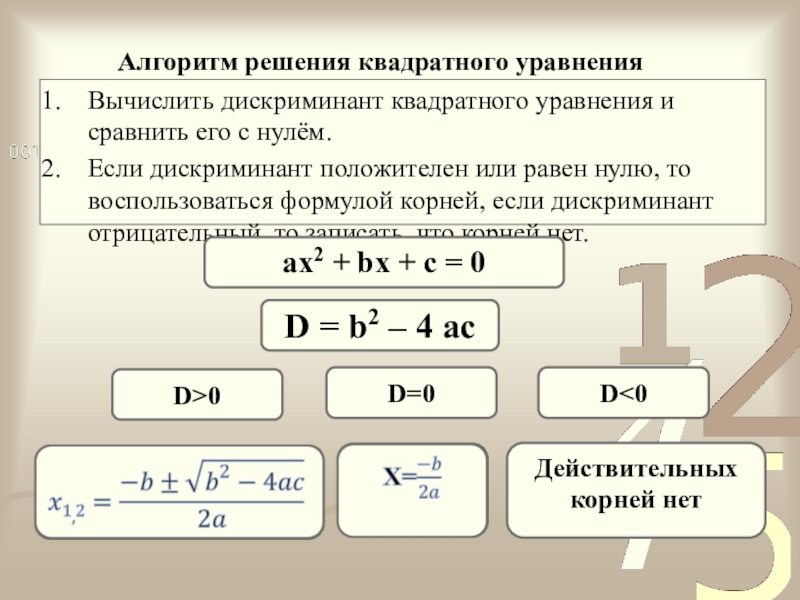
Слайд 16Алгоритм решения квадратного уравнения
Вычислить дискриминант квадратного уравнения и сравнить его с
Если дискриминант положителен или равен нулю, то воспользоваться формулой корней, если дискриминант отрицательный, то записать, что корней нет.
ax2 + bx + c = 0
D = b2 – 4 ac
D<0
D=0
D>0
Действительных корней нет
Слайд 18
Самостоятельные и контрольные работы по теме: «Квадратные уравнения»
Тест № 1. (контролирующего
1. Какое из уравнений является квадратным:
а) -3х² + 4/х = 0; б) -х² + 4х³ +8 = 0;
в) -5х + 3 = 0; г) 0,2х² + 13х + 10 = 0 ?
2. В квадратном уравнении: х² - 77х + 2 = 0 укажите его коэффициенты.
Ответы:
а) а =77, b =1, с =2 в) а =1, b = -77, с =2
б) а =77, b =2, с =77 г) а =1, b =77, с =-2
3. Какие из чисел – 4; -2; -1; 0; 3 являются корнями уравнения:
- 2х² + 6х = 0 ?
Ответы: а) -2; 0; б) 0;3; в) 3; -1; г) – 4; 0.
4. Найдите корни уравнения: 3а² - 75 = 0
5. Решите уравнение: (2х – 9)(х + 1) = (х –3)(х + 3)
6. При каком значении а корни уравнения:
х² +(а + 1)х + а - 8 = 0 являются противоположными числами?
Слайд 19
Самостоятельные и контрольные работы по теме: «Квадратные уравнения»
Тест № 2. (контролирующего
Вычислите дискриминант квадратного уравнения:
2х² - 5х + 3 = 0
Ответы: а) 49; б) -1; в) 1; г) 25
2. Определите, имеет ли квадратное уравнение:
х² + 7х + 6 = 0 корни если имеет, то сколько?
Ответы: а) 1 корень имеет; б) не имеет корней; в) имеет 2 корня
3. Найдите корни уравнения: х² +10х + 9 = 0
Ответы: а) -1; -9; б) -1; 9; в) -9;1; г) 1;9
4. Решите уравнение: 5х ² = 9х + 2
5. Найдите сумму корней уравнения:
х² +5х
_______ - 1 = 2
2
6. Один из корней уравнения: х2 -26 х + q = 0 равен12. Найдите другой корень и свободный член q.
Слайд 20
Самостоятельная работа №1.
Вариант 1.
Туристы отправляются на лодке к водопаду с намерением
Вариант 2.
Рыболов отправляется на лодке от пристани против течения реки с намерением вернуться назад через 5ч. Перед возвращением он хочет побыть на берегу 2 ч. На какое наибольшее расстояние он может отплыть, если скорость течения реки 2 км/ч, а собственная скорость лодки 6 км/ч?
Слайд 21Контрольная работа №1
1 вариант
№1Решите уравнение
а) 2х2+7х-9 = 0 а) 3х2+13х – 10 = 0
б) 3х2 = 18х б) 2х2-3х = 0
в) 100х2 – 16 = 0 в) 16х2 = 49
г) х2 - 16х +63 = 0 г) х2-2х-35=0
№2 Периметр прямоугольника равен 20 см. №2 Периметр прямоугольника равен 30 см.
Найдите его стороны, если известно, Найдите его стороны, если известно,
что площадь прямоугольника равна 24см2. что площадь прямоугольника равна 56см2.
№3 В уравнении х2+рх -18=0 один №3 Один из коней уравнения х2 + 11х +q =0
из его корней равен -9. равен -7. Найти другой корень и свободный
Найдите другой корень и коэффициент р член q.
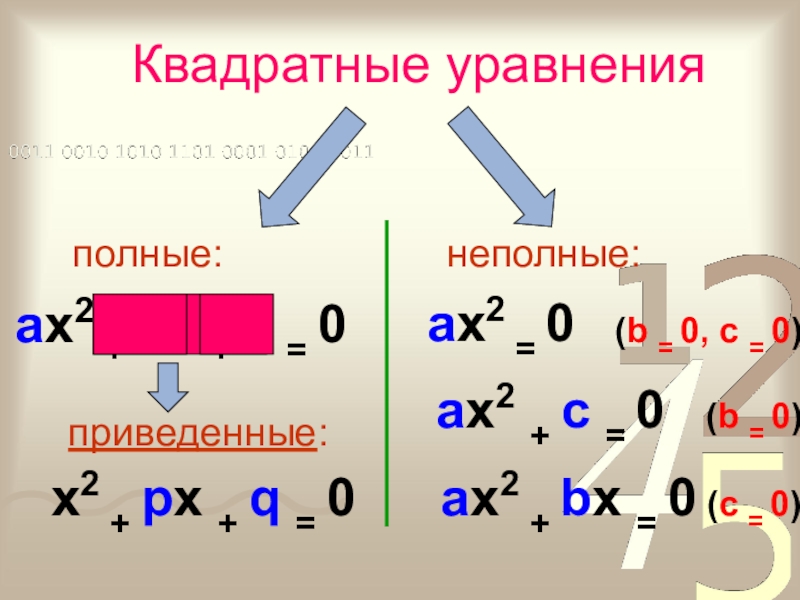
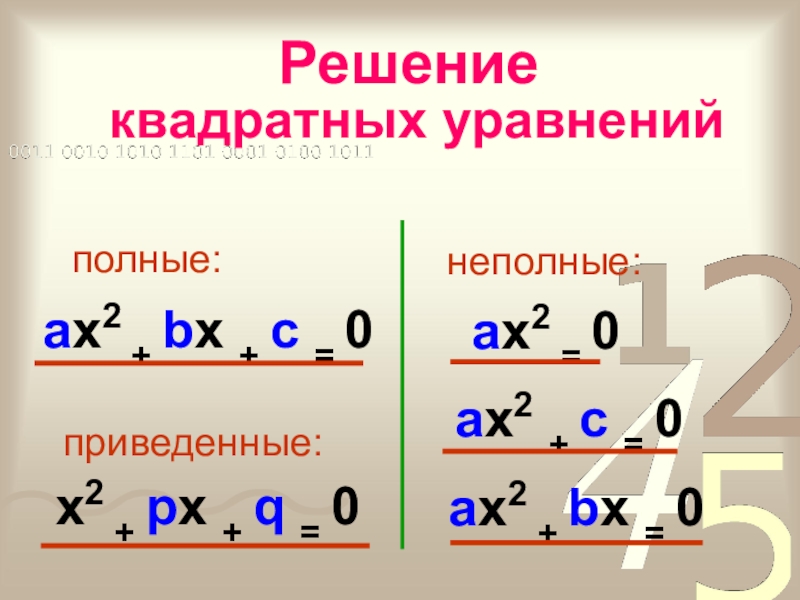
Слайд 22Квадратные уравнения
неполные:
ax2 + bx + c = 0
приведенные:
x2 + px +
ax2 + c = 0
ax2 + bx = 0
ax2 = 0
(b = 0, c = 0)
(b = 0)
(c = 0)
полные:
Слайд 27Литература
Т.А. Бурмистрова. Алгебра. Программы общеобразовательных учреждений. М.: Просвещение 2009г.
С.А. Теляковский. Алгебра-8.Учебник
Т.А. Иванова. Современный урок математики: теория, технология, практика.
П.И. Алтыпов. Тесты.7-9 классы. М.: Дрофа, 2005г.
Ю.Н. Макарычев, Н.Г. Миндюк. Дидактические материалы по алгебре для 8 класса. М.: Просвещение, 2002г.
А.П. Голобородько, А.П. Ершова. Самостоятельные и контрольные работы по алгебре и геометрии. М.: Илекса, 2002г.
Л.И. Мартышова. Контрольно-измерительные материалы. Алгебра: 8 класс. М.: ВАКО, 2010г.
Журнал. Математика в школе.
Газета. Первое сентября.