- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Мастер-класс Решение задач на движение
Содержание
- 1. Презентация Мастер-класс Решение задач на движение
- 2. Стандартная схема решения текстовой задачи состоит из
- 3. При решении этих задач принимают следующие допущения:
- 4. Формулы нахождения расстояния, скорости и времениФормула для
- 5. Типовые задачи на движениеПри решении задач часто
- 6. Если одно тело догоняет другое, то теперь
- 7. Задачки-минуткиЗадачка 1. Определите через какое время встретятся
- 8. Задача 1. Пароход прошел 4 км против
- 9. Решение задачи №1Получаем квадратное уравнение х2–37х+146,25=0 х1=4,5
- 10. Задача для самостоятельного решения
- 11. Задача №2 (№5.1.95 из сборника ГИА-2013)Теплоход идет
- 12. Решение задачи
- 13. Задача для самостоятельного решения (из сборника ГИА-2013)
- 14. Слайд 14
- 15. Задача 3. Расстояние между городами А и
- 16. Решение задачи №3
- 17. №4.1.97. Непослушный ребенок находится от отца на
- 18. Решение задачи
- 19. Итоги мастер-классаПовторили табличный способ систематизации данных задачи.
- 20. Спасибо за внимание
Слайд 1Мастер-класс «Решение текстовых задач на движение»
Подготовил: учитель математики Кондратьева А.Г.
Слайд 2Стандартная схема решения текстовой задачи состоит из нескольких этапов:
Обозначение буквами x,
Построение схем и составление таблиц.
Составление с помощью введенных переменных и известных из условия задачи величин уравнения или системы уравнений (в некоторых случаях – систем неравенств).
Решение полученного уравнения или системы уравнений.
Отбор решений, подходящих по смыслу задачи.
Слайд 3При решении этих задач принимают следующие допущения:
Если нет специальных оговорок, то
Повороты движущихся тел, переходы на новый режим движения считаются происходящими мгновенно.
Если тело с собственной скоростью х движется по реке, скорость течения которой равна у, то скорость движения тела по течению считается равной (х+у), а против течения – (х-у).
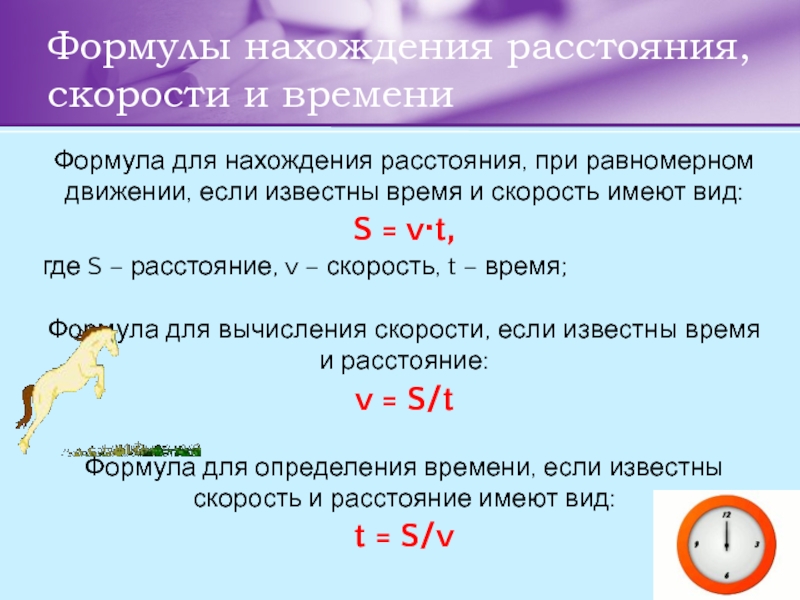
Слайд 4Формулы нахождения расстояния, скорости и времени
Формула для нахождения расстояния, при равномерном
где S – расстояние, v – скорость, t – время;
Формула для вычисления скорости, если известны время и расстояние: v = S/t
Формула для определения времени, если известны скорость и расстояние имеют вид: t = S/v
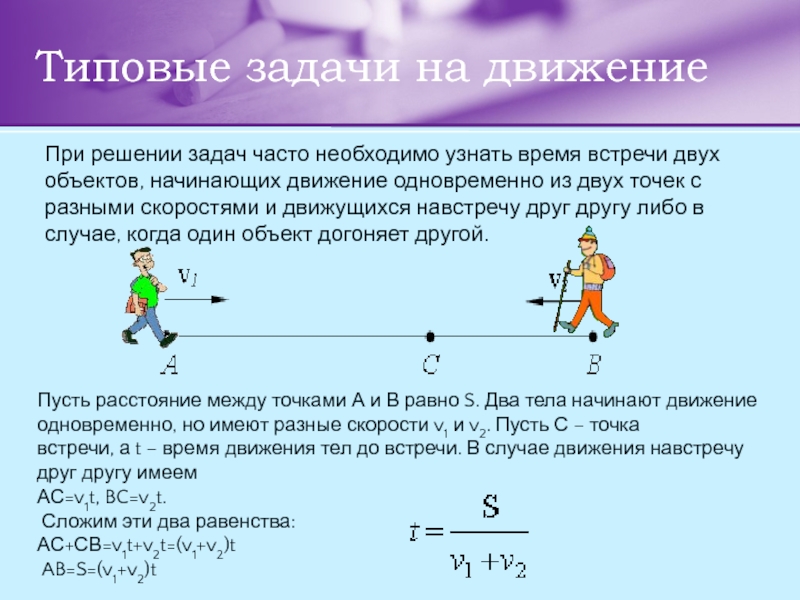
Слайд 5Типовые задачи на движение
При решении задач часто необходимо узнать время встречи
.
Пусть расстояние между точками А и В равно S. Два тела начинают движение одновременно, но имеют разные скорости v1 и v2. Пусть С – точка
встречи, а t – время движения тел до встречи. В случае движения навстречу друг другу имеем
АС=v1t, BC=v2t.
Сложим эти два равенства:
АС+СВ=v1t+v2t=(v1+v2)t
AB=S=(v1+v2)t
Слайд 6Если одно тело догоняет другое, то теперь получаем АС=v1t, BC=v2t.
Вычтем
АС–ВС=(v1–v2)t.
Так как АС–ВС=AB=S, то время, через которое первое тело догонит
второе, определяется равенством
Типовые задачи на движение
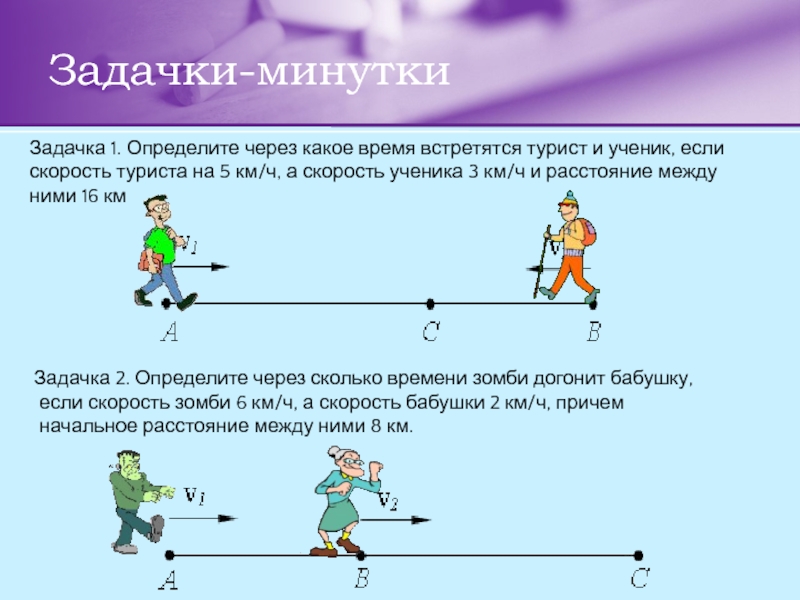
Слайд 7Задачки-минутки
Задачка 1. Определите через какое время встретятся турист и ученик, если
скорость туриста на 5 км/ч, а скорость ученика 3 км/ч и расстояние между
ними 16 км
Задачка 2. Определите через сколько времени зомби догонит бабушку,
если скорость зомби 6 км/ч, а скорость бабушки 2 км/ч, причем
начальное расстояние между ними 8 км.
Слайд 8Задача 1.
Пароход прошел 4 км против течения реки, а затем
течению, затратив на весь путь один час. Найдите собственную скорость парохода, если скорость течения реки равна 6,5 км/ч.
Пусть х км/ч – собственная скорость парохода.
Тогда (х+6,5) км/ч – скорость парохода по течению.
(х–6,5) км/ч – скорость парохода против течения.
Слайд 9Решение задачи №1
Получаем квадратное уравнение
х2–37х+146,25=0 х1=4,5 км/ч и х2=32,5 км/ч.
Осуществим отбор полученных
х1=4,5 км/ч не подходит по смыслу задачи (при такой скорости пароход не выплыл бы против течения).
Поэтому, собственная скорость парохода равна 32,5 км/ч.
Ответ: v=32,5 км/ч.
Слайд 11Задача №2 (№5.1.95 из сборника ГИА-2013)
Теплоход идет по течению реки в
Решение:
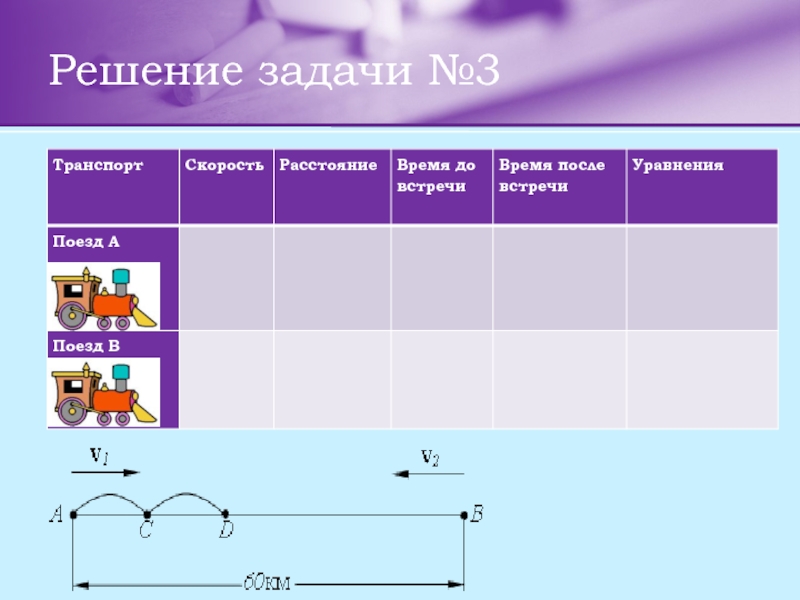
Слайд 15Задача 3.
Расстояние между городами А и В равно 60 км.
одновременно: один из А в В, другой из В в А. Пройдя 20 км, поезд, идущий из А в В, останавливается на полчаса, затем, пройдя 4 минуты, встречает поезд, идущий из В. Оба поезда прибывают к месту назначения одновременно. Найдите скорости поездов.
А
В
Слайд 17№4.1.97. Непослушный ребенок находится от отца на расстоянии 26 своих шагов.
Задача №4 (№4.1.97 из сборника ГИА-2013)
Схема решения:
1 выразить одни единицы измерения через другие, зная их соотношение.
2.определить скорость движения каждого
3.решить задачу на сближение по общей схеме
Слайд 19Итоги мастер-класса
Повторили табличный способ систематизации данных задачи.
Отработали навыки по созданию
Еще раз обратили внимание на то, что задача решается в единой системе измерений.
Отметили, что если уравнение, составленное к задаче, имеет два корня, то полученные решения требуют смысловой проверки.
Обратили внимание на то, что нельзя решать задачу «автоматически»; необходимо прежде всего внимательно ее прочитать, оценить в каких единицах измеряется каждая величина, данная в задаче, как эти величины связаны между собой и той величиной, которую следует найти, и только после этого, выбрав способ решения, приступить к самому решению.