- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Квадратные уравнения (8 класс)
Содержание
- 1. Презентация Квадратные уравнения (8 класс)
- 2. Цели урока: 1. Познакомиться с понятиями: квадратное
- 3. Из истории возникновения квадратных уравнений. Простые уравнения люди
- 4. Задача знаменитого индийского математика XII века БхаскарыНа
- 5. Квадратным уравнение называется уравнение вида:ax² + bx
- 6. Определите коэффициенты и свободные члены в уравнениях: Например:3х²
- 7. Определение неполного квадратного уравнения Вернёмся к задаче
- 8. Неполные квадратные уравнения бывают 3 видов:ax² +
- 9. Таблица решения неполных квадратных уравнений.
- 10. 1 группа 2 группа(0; 4)
- 11. Игра "Цепочка"1 ряд. 2 ряд.
- 12. В задаче Бхаскары мы получили следующее уравнение:х²
Слайд 2Цели урока:
1. Познакомиться с понятиями: квадратное уравнение и неполное квадратное
2. Научиться решать неполные квадратные уравнения.
3. Продолжать развивать интерес к математике.
Слайд 3Из истории возникновения квадратных уравнений.
Простые уравнения люди научились решать более трех
Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений было сформулировано в Европе в 1544 г. М.Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, который признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Именно в XVI – XVII вв. происходит бурное развитие науки, прежде всего в области математики и естествознания, и на этой основе складывается новое представление о Вселенной.
Слайд 4Задача знаменитого индийского математика XII века Бхаскары
На две партии разбившись,
Забавлялись обезьяны.
Часть
В роще весело резвилась.
С криком радостным часть восьмая
Воздух свежий оглашали.
Вместе сколько ты скажи мне,
Обезьян там в роще было?
Слайд 5Квадратным уравнение называется уравнение вида:
ax² + bx + c = 0
где х – переменная,
a – первый коэффициент,
b – второй коэффициент,
c – свободный член.
Как вы думаете , почему уравнение такого вида называется квадратным?
Слайд 6Определите коэффициенты и
свободные члены в уравнениях:
Например:
3х² + 2х + 7
а = 3, b=2 c = 7.
5х² + х – 2 = 0
a = 5, b = 1, c = -2
х² + 2х + 3 = 0
a = 1, b = 2, c = 3
х² + 1 – 3х = 0
a = -1, b = -3, c = 1
-7х +2х² + 2 = 0
a = 2, b = -7, c = 2
-6х - 2х² - 5 = 0
a = -2, b = -6, c = -5
МОЛОДЦЫ!
Слайд 7Определение неполного квадратного уравнения
Вернёмся к задаче Бхаскары.
Определим коэффициенты в уравнении:
a = 1, b = -56, c = 0
Если в квадратном уравнении
ax² + bx + c = 0 (а ≠ 0),
хотя бы один из коэффициентов равен 0 (кроме а), то такое уравнение называется
неполным квадратным уравнением.
Слайд 8Неполные квадратные уравнения бывают 3 видов:
ax² + c = 0 (c
Рассмотрим пример:
5х² - 125 = 0, 4х² + 64 = 0,
5х² = 125, 4х² = - 64,
х² = 25, х² = - 64,
х = ±5. корней нет.
Ответ: ±5. Ответ: корней нет.
ax² + bx = 0 (b ≠ 0)
Рассмотрим пример:
4х² + 9х = 0,
х(4х + 9) = 0,
Х = 0 или 4х + 9 = 0,
4х = -9,
х = -2,5,
Ответ: -2,5; 0.
3. ax² = 0
Рассмотрим пример:
5х² = 0,
х = 0.
Ответ: 0.
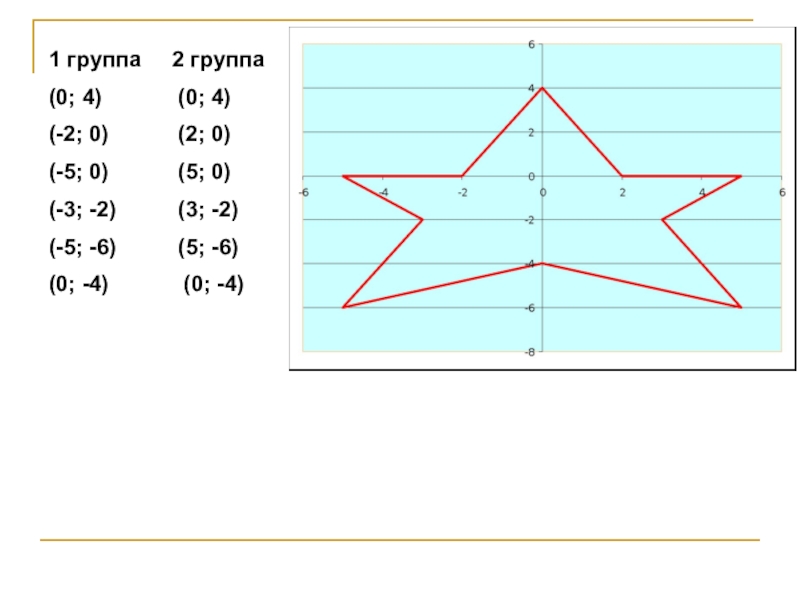
Слайд 101 группа 2 группа
(0; 4) (0;
(-2; 0) (2; 0)
(-5; 0) (5; 0)
(-3; -2) (3; -2)
(-5; -6) (5; -6)
(0; -4) (0; -4)
Слайд 11Игра "Цепочка"
1 ряд. 2 ряд. 3 ряд.
1.
2. нет корней. 2. нет корней. 2. нет корней.
3. х=0, х=0,75 3. х=0, х=2,5 3. х=0, х=2/3
4. х=0, х=1,4 4. х=0, х=2,25 4. х=0, х=3
5. х=0 5. х=0 5. х=0
Слайд 12В задаче Бхаскары мы получили следующее уравнение:
х² - 56х = 0,
х(х
х = 0 или х – 56 = 0,
х = 56.
Ответ 56 обезьян.
Итог урока.
С какими новыми уравнениями мы познакомились?
Какой вид имеют квадратные уравнения?
Какое уравнение называется неполным квадратным уравнением?
Домашнее задание: придумать к каждому виду неполного
квадратного уравнения примеры.