- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Кез келген тригонометриялық функциялар
Содержание
- 1. Презентация Кез келген тригонометриялық функциялар
- 2. Нақты сан мен шеңбер нүктесінің арасындағы сәйкестігі
- 3. Дөңгелек координатасыСан түзуі мен санды шеңбердің ұқсастығына
- 4. СMF BE O
- 5. Санды шеңберТригонометриялық функцияларды енгізу үшін сан түзуінен
- 6. Санды шеңбердің В нүктесіне сәйкес барлық сандарды
- 7. уОАВIIIIIIIVх хАу ВО
- 8. Анықтама:В нүктесінің ординатасының ОВ радиусқа қатынасы
- 9. Тригонометриялық функциялар
- 10. Анықталу облысы Sin α және cosα функцияларының
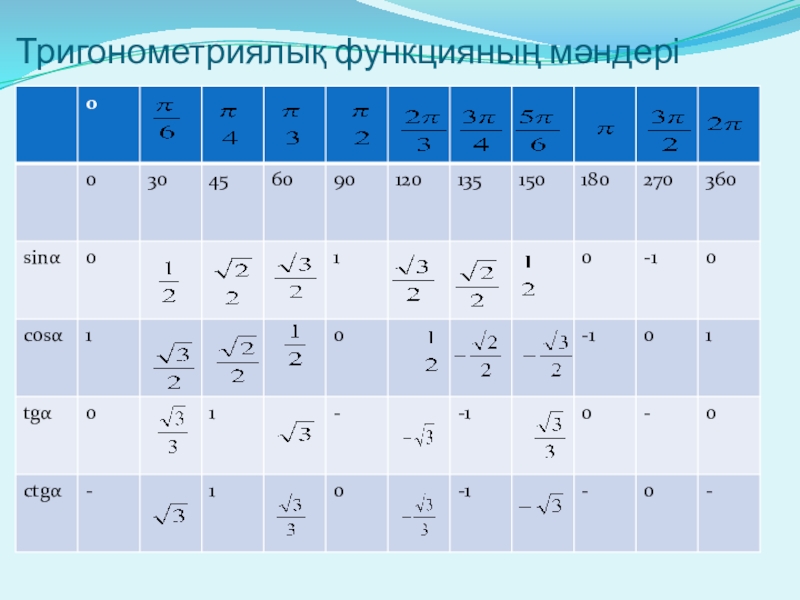
- 11. Тригонометриялық функцияның мәндері
- 12. Есептер шығару 274, 275, 276, 277, 278 Үйге тапсырма 279, 280, 282
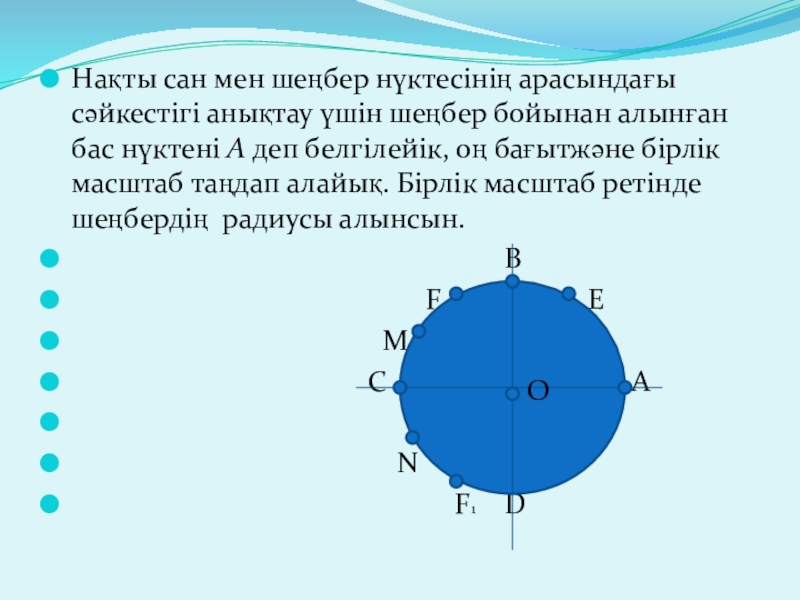
Слайд 2Нақты сан мен шеңбер нүктесінің арасындағы сәйкестігі анықтау үшін шеңбер бойынан
B
F В E
M
C A
N
F1 D
O
Слайд 3Дөңгелек координатасы
Сан түзуі мен санды шеңбердің ұқсастығына сүйеніп, шеңбер бойындағы М
Сондықтан кез келген нақты санға шеңбердің белгілі бір нүктесі сәйкес келеді.
Слайд 4С
M
F
B
E
O
N
F 1 D
Кез келген нақты санға шеңбердің белгілі бір нүктесі сәйкес келеді. Демек, 0 санына А нүктесінің бастапқы нүктесі сәйкес, 1 санына АЕ = 1 радиан болатын доғаның соңы Е нүктесі сәйкес, 2 санына АF =2 радиан болатын доғаның соңы F нүктесі сәйкес, 6,5 санына 6,5 радианға тең доғаның соңы болып табылатын қайсыбір нүкте сәйкес келеді. Әрине, кез келген теріс санға теріс доғаның соңы болатын нүкте сәйкес келеді. Мысалы, z = -2 санына АF 1 = -2 радиан болатын доғаның соңы F 1 нүктесі сәйкес келеді.
Слайд 5Санды шеңбер
Тригонометриялық функцияларды енгізу үшін сан түзуінен басқа жаңа математикалық үлгі
Сонымен, сандар мен шеңбер нүктелері арасындағы сәйкестікті табу әдісін алдық. Әрі қарай мұндай сан түзуі болатын шеңберді санды шеңбер деп атайтын боламыз.
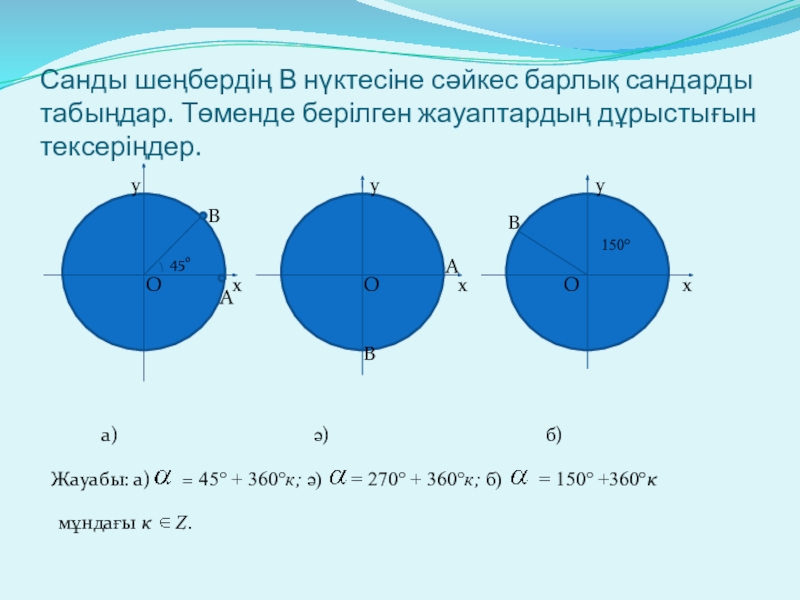
Слайд 6Санды шеңбердің В нүктесіне сәйкес барлық сандарды табыңдар. Төменде берілген жауаптардың
у
х
у
х
х
у
В
А
О
45º
В
А
О
О
В
150°
а)
ә)
б)
Жауабы: а)
= 45° + 360°к; ә)
= 270° + 360°к; б)
= 150° +360°к
мұндағы к Z.
Слайд 7у
О
А
В
I
II
III
IV
х
х
А
у
В
О
А
х
у
О
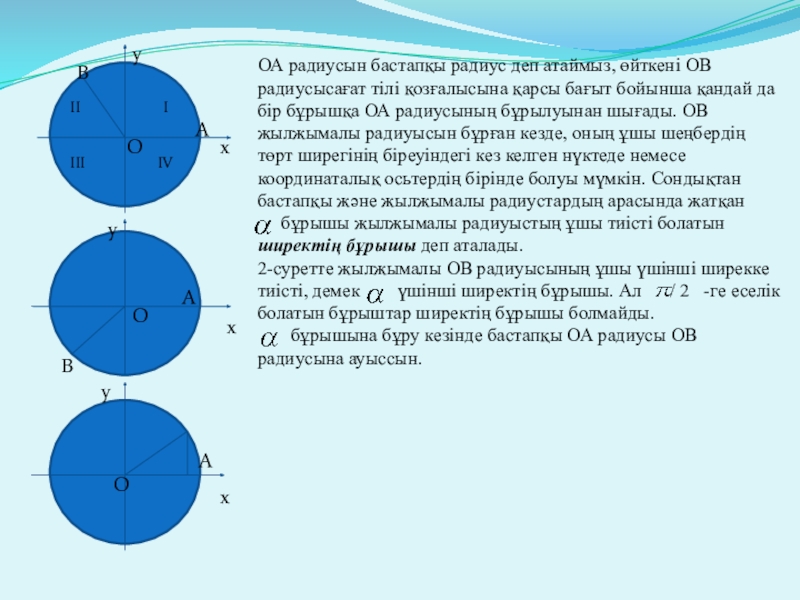
ОА радиусын бастапқы радиус
бұрышы жылжымалы радиуыстың ұшы тиісті болатын ширектің бұрышы деп аталады.
2-суретте жылжымалы ОВ радиуысының ұшы үшінші ширекке тиісті, демек үшінші ширектің бұрышы. Ал / 2 -ге еселік болатын бұрыштар ширектің бұрышы болмайды.
бұрышына бұру кезінде бастапқы ОА радиусы ОВ радиусына ауыссын.
Слайд 8Анықтама:
В нүктесінің ординатасының ОВ радиусқа қатынасы бұрышының
В нүктесінің абсциссасының ОВ радиусқа қатынасы қатынасы бұрышының косинусы деп аталады.
В нүктесінің ординатасының абсциссаға қатынасы бұрышының тангенсі деп аталады.
В нүктесінің абсциссасының ординатаға қатынасы бұрышының котангенсі деп аталады.