Презентация, доклад к выступлению на НПК 10 способов решения квадратных уравнений

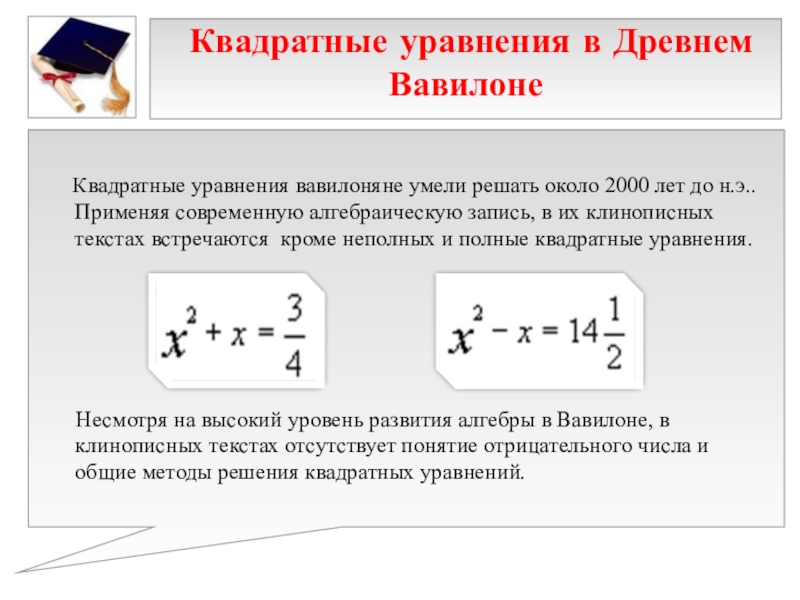
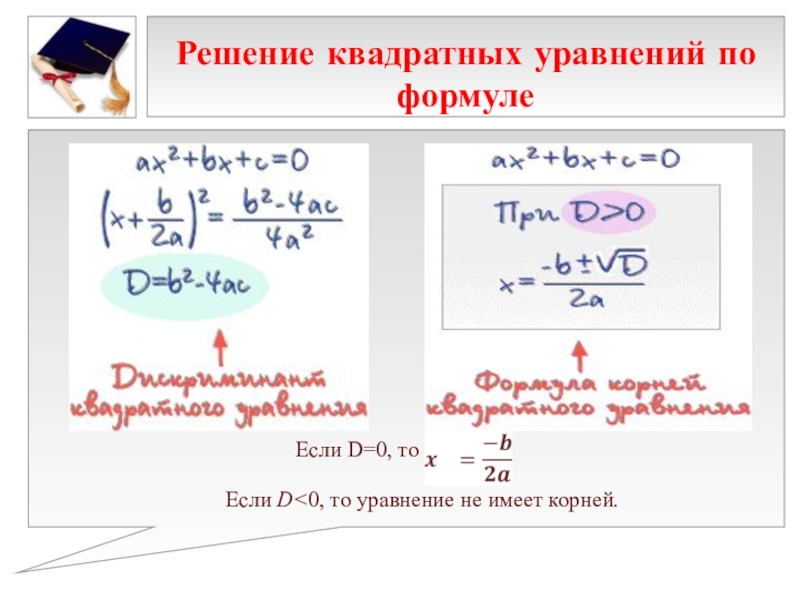
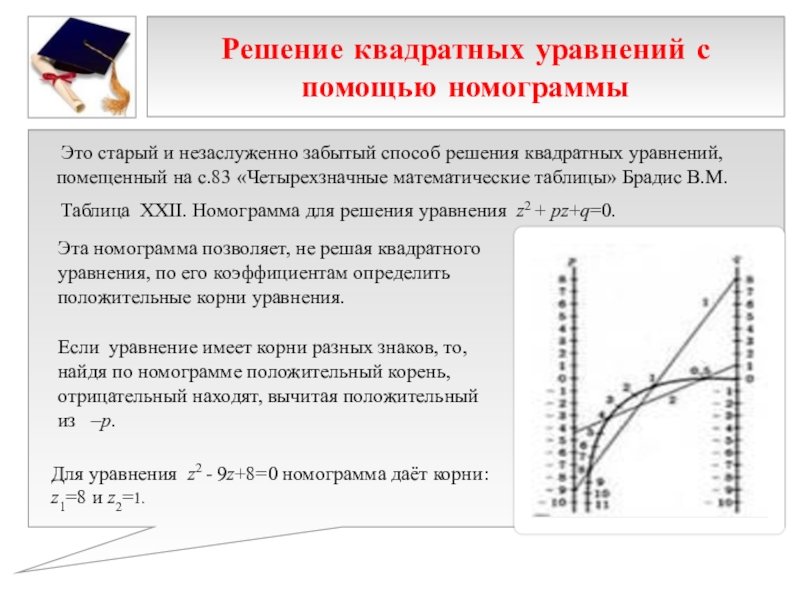
Авторы: Тайдонова Анастасия Михайловна,
Тайдонова Виктория Михайловна ,
учащиеся 8 А класса
Руководитель: Загородних Ольга Иосифовна,
учитель математики
.
п. Копьёво, 2016 г.

Муниципальное бюджетное общеобразовательное учреждение
«Копьёвская средняя общеобразовательная школа
с углублённым изучением отдельных предметов»

из истории квадратных уравнений, изложить 10 способов решения квадратных уравнений (стандартные и нестандартные)

Объект исследования: квадратные уравнения.

Предмет исследования: способы решения квадратных уравнений.

Гипотеза: для некоторых квадратных уравнений применение нестандартных способов решения позволяет устно найти корни этого уравнения.

Квадратные уравнения вавилоняне умели решать около 2000 лет до н.э.. Применяя современную алгебраическую запись, в их клинописных текстах встречаются кроме неполных и полные квадратные уравнения.




Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратных уравнений.

задач, решаемых при помощи составления уравнений.
Одна из его задач. «Найти 2 числа, зная, что их сумма равна 20, а произведение – 96.» Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведения равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10+x, другое же меньше, т.е. 10-x. Отсюда уравнение (10+x)(10-x)=96, или же 100 - x2=96, x2 - 4=0. Отсюда x=2. Одно из искомых чисел равно 12, другое 8.
Решение x = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.

уже в трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой.
Одна из задач знаменитого индийского математика XII века Бхаскары:
«Обезьянок резвых стая Всласть поевши, развлекалась. Их в квадрате часть восьмая На полянке забавлялась. А двенадцать по лианам…

Соответствующее задаче уравнение


Бхаскара пишет под видом
x2 - 64x= -768, прибавляет к обеим частям 322 , получая затем: x2 - 64x+322= -768+1024, (x - 32)2 = 256, x - 32= ±16, x1=16, x2=48.

Стали прыгать повисая… Сколько было обезьянок Ты скажи мне, в этой стае?»

Трактат ал-Хорезми является первой дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения. Его решения ,конечно, не совпадает полностью с нашим.
Задача. «Квадрат и число 21 равны 10 корням. Найти корень.» (подразумевается корень уравнения x2+21= 10x) .
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Автор первый в Европе подошёл к введению отрицательных чисел.





Лишь в XVII в. благодаря трудам Декарта, Ньютона и других учёных способ решения квадратных уравнений принимает современный вид.

Квадратные уравнения общего вида надо привести к виду: A(x)∙B(x)=0, где A(x) и B(x) - многочлены относительно x.

Пример. Решить уравнение 4х2+5х+1=0. Слагаемое 5х представим в виде суммы двух слагаемых 4х и х, получим 4х2+4х+х+1=0. Применим способ группировки, уравнение примет вид 4х(х+1)+(х+1)=0. Левую часть уравнения раскладываем на множители (х+1)(4х+1)=0. Следовательно, х+1=0 или 4х+1=0; х1= -1; х2= - 0,25.
Ответ: х1= -1, х2= - 0,25

х2 + 6х - 7 = 0.
Выделим из трехчлена х2 + 6х -7 квадрат двучлена:
х2 + 2∙3х+ 9-9-7=0,
(х +3)2 – 16 = 0,
(х +3)2 = 16,
х +3 = 4, х + 3 = -4,
х = 1, х =-7.
Ответ: 1; -7.

(a + b)2 = a2 + 2ab + b2,
(a - b)2 = a2 - 2ab + b2.

Если D=0, то

Если D<0, то уравнение не имеет корней.

корнями, впервые сформулировал знаменитый французский математик Франсуа Виет в 1591 г.

Теорема. Если х1 и х2 - корни уравнения х2+px+q=0, то х1+х2 =-p и х1∙х2 = q.

Теорема, обратная теореме Виета. Если числа m и n таковы, что m+n= – p, m∙n=q, то эти числа являются корнями уравнения х2+px+q = 0.

Теорема Виета и обратная ей теорема позволяют:
1) проверить правильность найденных корней уравнения x²+px+q = 0;
судить о знаках и абсолютной величине корней уравнения x²+px+q = 0;
3) устно находить целые корни уравнения x²+px+q = 0;
4) составлять квадратные уравнения с заданными корнями.

а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда дискриминант является точным квадратом целого числа и можно легко найти корни уравнения, используя теорему, обратную теореме Виета.
Пример. Решить уравнение: 2х2– 11х+5=0.
Перебросим коэффициент 2 к свободному члену. Получим новое уравнение y2– 11y+10=0. D=81>0, по теореме, обратной теореме Виета, подбором находим корни y = 10; y2=1.
Корни уравнения необходимо поделить на 2, получаем корни исходного уравнения: х1 = 5; х2 = 0,5
Ответ: х1= 5; х2 = 0,5.

в квадратном уравнении ax2 + bx + c = 0 сумма коэффициентов равна нулю a+b+c=0, то один из корней равен 1, а второй равен c/a.
Пример. Решить уравнение 137х2 +20х -157= 0.
a+b+c=137+20-157=0, х1 =1, х2 = c/a = -157/137.
Ответ: 1; -157/137.
2) Если в квадратном уравнении ax2 + bx + c = 0 сумма первого коэффициента и свободного члена равна второму коэффициенту a+c=b, то один из корней равен -1, а второй равен - c/a.
Пример. Решить уравнение 127х2 +272х + 145 =0. a+c=127+145=272=b, х1= -1, х2 = - c/a = - 145/127 . Ответ: х1= -1, х2 = - 145/127.

с=а, то корни квадратного уравнения равны
х = –а и х = – 1/a.
2) Если а2+1=-b и с=а, то корни квадратного уравнения равны
х = а и х = 1/a.
3) Если а2–1= b и а=-c, то корни квадратного уравнения равны
х = –а и х = 1/a.
4) Если а2–1= -b и а=-с, то корни квадратного уравнения равны
х = а и х = –1/a .
Пример. Решить уравнение: 17х2 +288х –17 = 0,
a =17, b=288, c=-17, а2–1= 289-1=288=b, а= 17= -c, значит, по свойству 3 получим корни х = –17 и х =1/17 .

ax2 + bx + c = 0

= 0 графическим способом необходимо построить два графика:
y=ax2 и y=-bx-c.
Абсциссы точек пересечения графиков и будут корнями уравнения.
1)Если графики пересекаются в двух точках, то уравнение имеет два корня. 2) Если графики пересекаются в одной точке, то уравнение имеет один корень. 3)Если графики не пересекаются, то уравнение корней не имеет.

Решить уравнение x2 – x –1=0 графическим способом. Для этого построим два графика: y=x2 и y=x+1.

Ответ:

+ bх + с = 0 (а ≠ 0) можно рассматривать как абсциссы точек пересечения оси Ох и окружности с центром Q (- ; ), проходящей через точку A(0; 1).

и незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83 «Четырехзначные математические таблицы» Брадис В.М.

Таблица XXII. Номограмма для решения уравнения z2 + pz+q=0.

Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить положительные корни уравнения.

Если уравнение имеет корни разных знаков, то, найдя по номограмме положительный корень, отрицательный находят, вычитая положительный из –p.

Для уравнения z2 - 9z+8=0 номограмма даёт корни: z1=8 и z2=1.