- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Различные способы решения квадратных уравнений
Содержание
- 1. Презентация к уроку Различные способы решения квадратных уравнений
- 2. 1. Уравнение второй степени.2. Сколько корней имеет
- 3. «Человеку, изучающему алгебру, часто полезнее решить одну
- 4. Различные способы решения квадратных уравнений
- 5. Когда уравненье решаешь, дружок,Ты должен найти у
- 6. Слайд 6
- 7. Задание 1: Решите квадратные уравнения :1.
- 8. ответы:
- 9. Уравнение, вида х2+pх+q=0, называется приведённым.
- 10. Задание 2. Решите приведённые квадратные уравнения по теореме, обратной теореме Виета. х2+10х+9=0, х2+7х+12=0, х2-10х-24=0, х2-16х+60=0.
- 11. ответы:
- 12. Решить квадратное уравнение можно способом
- 13. Задание 3: Решите уравнения, используя метод «переброски»:1. 2х2-9х+9=0,2. 10х2-11х+3=0,3. 3х2+11х+6=0,4. 4х2+12х+5=0. .
- 14. ответы1. 2х2-9х+9=02. 10х2-11х+3=03. 3х2+11х+6=04. 4х2+12х+5=0х1=1,5 , х2=3.х1=0,5 ,х2=0,6.х1=-3,х2=- .х1=-2,5,х2=-0,5.
- 15. Пусть дано квадратное уравнение ах2+вх+с=0, где
- 16. 1. 5х2-7х+2=0;2. 3х2+5х-8=0;3. 11х2+25х-36=0;4.
- 17. 1. 5х2-7х+2=02. 3х2+5х-8=03. 11х2+25х-36=04.
- 18. Пятый способ: Метод выделения полного
- 19. 1. х2-10х+24=0;2. х2-8х+15=0;3. х2+6х+8=0;4.
- 20. ответы:х1=6,х2= 4 Х1=3,х2= 5 х1=
- 21. Разложение левой части уравнения на множители. Решим
- 22. 1. х2-8х+15=0;2. х2-
- 23. ответы:х1=3,х2= 5.х1=10,х2= 2.х1=1,х2= 3.х1=-4,х2= -2. 1.
- 24. Седьмой способ: Графическое решение квадратного
- 25. Задание 7:
- 26. Решение задания 7:
- 27. Восьмой способ: Решение квадратных уравнений
- 28. Девятый способ: Решение квадратных уравнений
- 29. Десятый способ: Геометрический способ решения
- 30. Выберите утверждение, которое соответствовало вашему настроению на
- 31. Домашнее задание:Из учебника подобрать по два уравнения к каждому из предложенных способов и решить их.
Слайд 1Прозвенел звонок для нас.
Все зашли спокойно в класс.
Встали все
Поздоровались учтиво.
Тихо сели, спинки прямо.
Вижу, класс наш хоть куда.
Мы начнём урок, друзья.
Слайд 21. Уравнение второй степени.
2. Сколько корней имеет квадратное уравнение, если D
3. Равенство с переменной?
4. От чего зависит количество корней квадратного уравнения?
5. Как называется квадратное уравнение, у которого первый коэффициент равен 1?
6. Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?
7. Что значит решить уравнение?
Слайд 3«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу
У. Сойер
Слайд 5Когда уравненье решаешь, дружок,
Ты должен найти у него корешок.
Значение буквы проверить
Поставь в уравненье его осторожно.
Коль верное равенство выйдет у вас,
То корнем значенье зовите тотчас.
О.Севостьянова
Слайд 7Задание 1: Решите квадратные уравнения :
1. 2х2-5х+2=0,
2. 6х2+5х+1=0,
3. 2х2-3х+2=0,
4. 4х2-12х+9=0.
Слайд 8 ответы:
х1= ½, х2=2.
х1= -½, х2= -⅓.
решений нет.
х1=1,5, х2=1,5.
1. 2х2-5х+2=0
2. 6х2+5х+1=0
3. 2х2-3х+2=0
4. 4х2-12х+9=0
Слайд 9 Уравнение, вида х2+pх+q=0, называется приведённым. Его корни можно найти
х1+х2=-p,
х1∙х2=q.
Например,
уравнение х2-3х+2=0
имеет корни х1=2, х2=1
так как х1+х2=3, х1∙х2=2.
Второй способ:
Слайд 10Задание 2. Решите приведённые квадратные уравнения по теореме, обратной теореме Виета.
х2+7х+12=0,
х2-10х-24=0,
х2-16х+60=0.
Слайд 11 ответы:
х1=-9,х2=-1.
х1=-4,х2=-3.
х1=12,х2=-2.
х1=10,х2=6
х2+10х+9=0
х2+7х+12=0
х2-10х-24=0
х2-16х+60=0
Слайд 12 Решить квадратное уравнение можно способом «переброски». Этот способ применяют,
Например: Решим уравнение 2х2-11х+15=0.
«Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение: у2-11у+30=0.
По теореме, обратной теореме Виета у1= 5,у2= 6. тогда х1=у1/2, х2=у2/2; т.е. х1=2,5 , х2=3.
Третий способ:
Слайд 13Задание 3: Решите уравнения, используя метод «переброски»:
1. 2х2-9х+9=0,
2. 10х2-11х+3=0,
3. 3х2+11х+6=0,
4. 4х2+12х+5=0.
.
Слайд 14 ответы
1. 2х2-9х+9=0
2. 10х2-11х+3=0
3. 3х2+11х+6=0
4. 4х2+12х+5=0
х1=1,5 , х2=3.
х1=0,5 ,х2=0,6.
х1=-3,х2=- .
х1=-2,5,х2=-0,5.
Слайд 15Пусть дано квадратное уравнение ах2+вх+с=0, где
1.Если а+в+с=0(т.е.сумма коэффициентов
уравнения равна нулю), то х1=1,х2=с/а.
Например: 345х2-137х-208=0 (345-137-208=0), значит,
х1= 1,х2= - 208/345.
2.Если а-в+с=0 (или в=а+с), то х1=-1,х2= - с/а.
Например, 313х2+326х+13=0 (326=313+13), значит
х1=-1,х2=-13/313.
Четвёртый способ:
Свойства коэффициентов квадратного уравнения.
Слайд 161. 5х2-7х+2=0;
2. 3х2+5х-8=0;
3. 11х2+25х-36=0;
4. 11х2+27х+16=0.
Задание
Слайд 171. 5х2-7х+2=0
2. 3х2+5х-8=0
3. 11х2+25х-36=0
4. 11х2+27х+16=0
ответы:
х1=1,х2=
х1=1,х2=- .
х1=1,х2=- .
х1=-1,х2=- .
Слайд 18
Пятый способ:
Метод выделения полного квадрата.
Решим уравнение
Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2• х • 3.
В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3.
Для этого чтобы получить полный квадрат, нужно прибавить 9 и отнять 9
( х2 + 2• х • 3 + 9 ) – 9 - 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 - 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 = 4 или х + 3 = -4
х1 = 1
х2 = -7.
Слайд 191. х2-10х+24=0;
2. х2-8х+15=0;
3. х2+6х+8=0;
4. х2-16х+ 60=0.
Задание 5: Решите квадратные уравнения методом «выделения полного квадрата»:
Слайд 20 ответы:
х1=6,х2= 4
Х1=3,х2= 5
х1= -4,х2=-2
х1=10,х2=6
1. х2-10х+24=0
2. х2-8х+15=0
3. х2+6х+8=0
4. х2-16х+ 60=0
Слайд 21Разложение левой части уравнения на множители.
Решим уравнение х2 +
Разложим левую часть на множители:
х2 + 10х - 24 = х2 + 12х - 2х - 24 =
=х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
получим уравнение:
(х + 12)(х - 2) = 0
х = - 12 х = 2
Шестой способ:
Слайд 221. х2-8х+15=0;
2. х2- 12х+20=0;
3. х2-
4. х2+6х+8=0.
Задание 6: решите квадратное уравнение разложением левой части на множители:
Слайд 23
ответы:
х1=3,х2= 5.
х1=10,х2= 2.
х1=1,х2= 3.
х1=-4,х2= -2.
1. х2-8х+15=0;
2.
3. х2- 4х+3=0;
4. х2+6х+8=0.
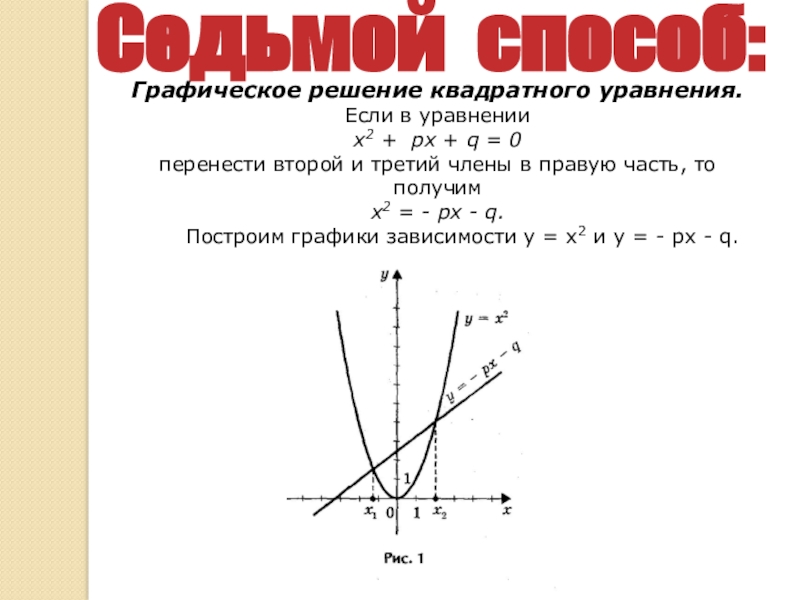
Слайд 24 Седьмой способ:
Графическое решение квадратного уравнения.
Если в
х2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
х2 = - px - q.
Построим графики зависимости у = х2 и у = - px - q.
Слайд 26
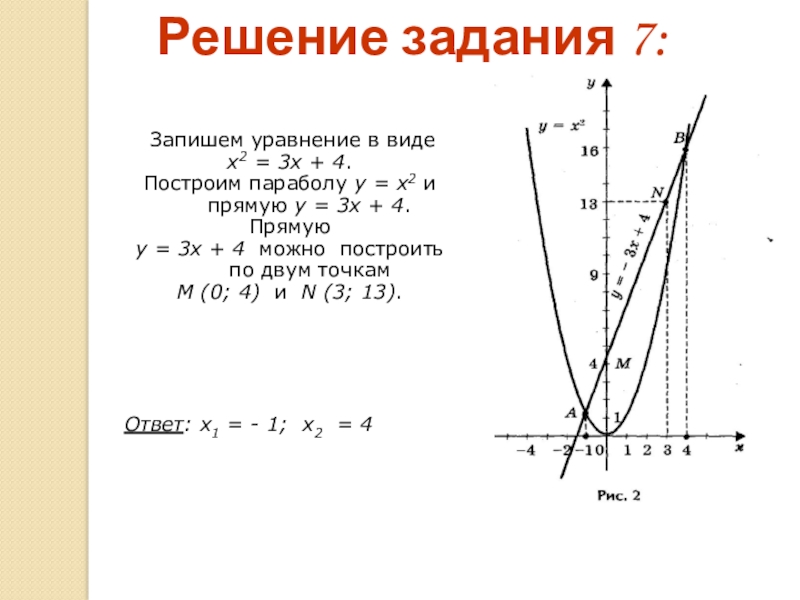
Решение задания 7:
Запишем уравнение в
х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4.
Прямую
у = 3х + 4 можно построить по двум точкам
М (0; 4) и N (3; 13).
Ответ: х1 = - 1; х2 = 4
Слайд 27 Восьмой способ:
Решение квадратных уравнений с помощью циркуля
нахождения корней квадратного уравнения
ах2 + bх + с = 0 с помощью циркуля и линейки .
Тогда по теореме о секущих имеем
OB • OD = OA • OC,
откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Слайд 28
Девятый способ:
Решение квадратных уравнений с помощью
z2 + pz + q = 0.
Криволинейная шкала номограммы построена по формулам
Полагая ОС = р, ED = q, ОЕ = а
Из подобия треугольников САН и CDF
получим пропорцию
Слайд 29 Десятый способ:
Геометрический способ решения квадратных уравнений.
• Примеры.
1)
В оригинале эта задача формулируется следующим образом :
«Квадрат и десять корней равны 39» (рис.15).
Для искомой стороны х первоначального
квадрата получим
Слайд 30Выберите утверждение, которое соответствовало вашему настроению на уроке:
Перепрыгивающему пропасть не следует
О, монах, ты идешь трудной дорогой.
Учиться, обучая.
Ах, как я устал от этой суеты.
Без труда не вытащишь рыбку из пруда.