В.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Решение систем уравнений второй степени с двумя переменными(9 класс)
Содержание
- 1. Презентация к уроку по теме Решение систем уравнений второй степени с двумя переменными(9 класс)
- 2. «Дорогу осилит идущий, а математику – мыслящий»Девиз урока:
- 3. Цель урока:систематизировать знания и умения по теме
- 4. Способы решения систем уравнений с двумя переменнымиГрафический способСпособ подстановки Способ сложения
- 5. Графический способКак решается система графическим способом?Почему координаты
- 6. Графический способпостроить графики уравнений в одной координатной
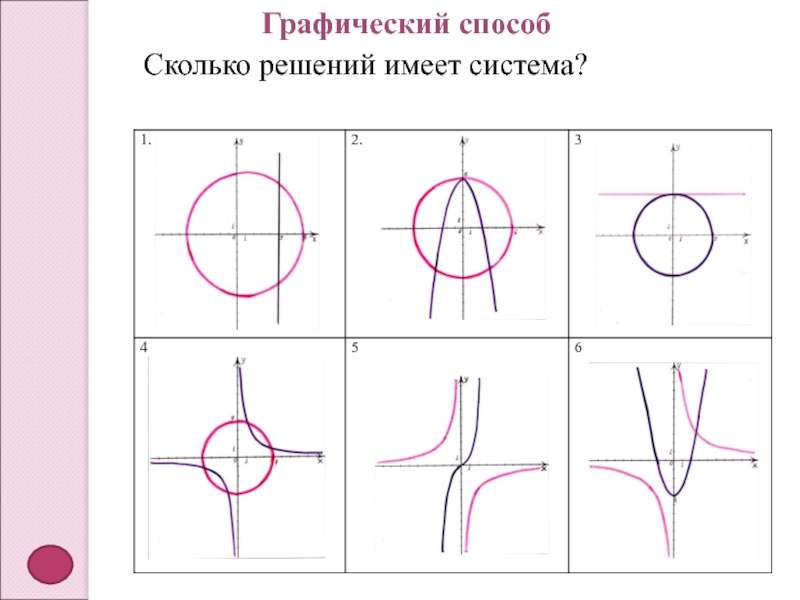
- 7. Графический способСколько решений имеет система?
- 8. Количество точек пересечения графиков и решений уравнений
- 9. Графический способЗадание 1. Совместить графики уравнений с формулами, которыми они задаются
- 10. Совмещение графиков уравнений с формулами, которыми они задаются
- 11. Графический способСамостоятельная работа1
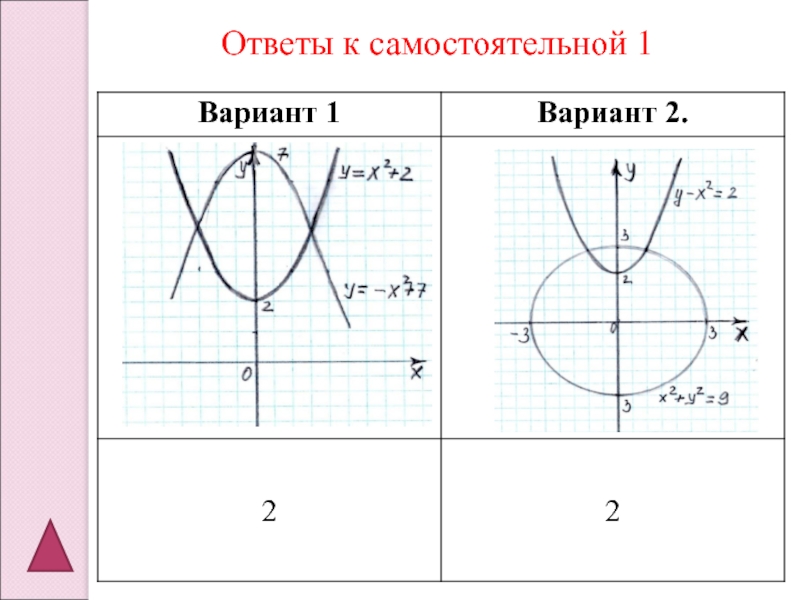
- 12. Ответы к самостоятельной 1
- 13. Cпособ подстановки Как решить систему способом подстановки?Есть
- 14. Cпособ подстановки Выражают из какого-нибудь уравнения системы
- 15. Задание 2. Выразите переменную y через через переменную xСпособ подстановки
- 16. Выражение переменной у через x
- 17. Способ подстановкиЗадание 3. Решите системы уравнений
- 18. Ответы к системам
- 19. Способ сложенияКак решить систему способом сложения?Как записать решение системы?
- 20. Способ сложенияУмножают почленно уравнения системы, подбирая множители
- 21. Самостоятельная работа 2Решите системы методом сложения
- 22. Ответы к самостоятельной работе 2
- 23. Слайд 23
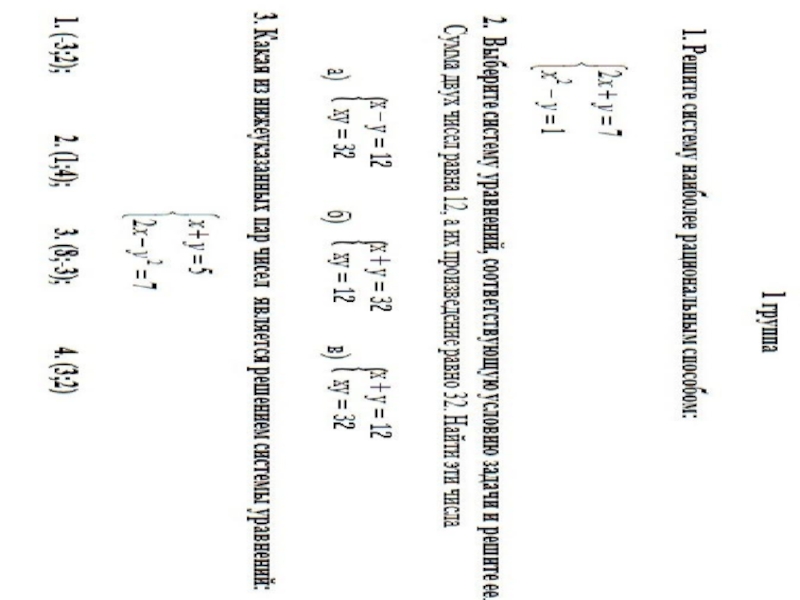
- 24. 1 группа (2;3) ; (-4;15) 4 и 8 (8;-3)
- 25. Слайд 25
- 26. 2 группа1. (-7; 11) (3;1)2. 4 и 53. ( -8; 6)
- 27. Слайд 27
- 28. 3 группаРешений нет а) ( 30; 26)
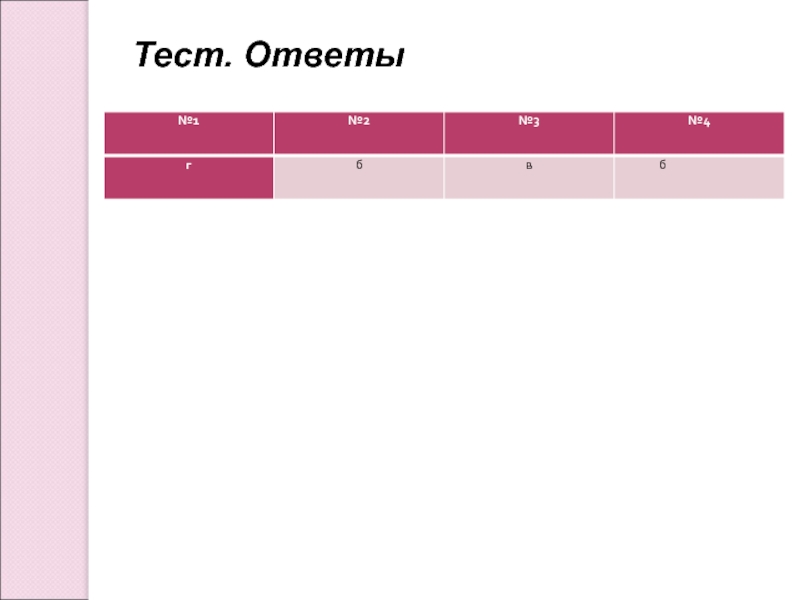
- 29. Тест. Ответы
- 30. Домашнее задание: п.18-19, с.109-112, № 433(б), 448(б), 440(б), 443(б)
«Дорогу осилит идущий, а математику – мыслящий»Девиз урока:
Слайд 3Цель урока:
систематизировать знания и умения по теме решение систем уравнений второй
степени с двумя переменными,
решать системы различными способами и
подготовиться к контрольной работе.
решать системы различными способами и
подготовиться к контрольной работе.
Слайд 4Способы решения систем уравнений с двумя переменными
Графический способ
Способ подстановки
Способ сложения
Слайд 5Графический способ
Как решается система графическим способом?
Почему координаты точек пересечения являются решениями
системы уравнений?
Как записывается решение системы уравнений, если она решается графическим способом?
От чего зависит количество решений системы уравнений при графическом способе?
Сколько точек пересечения имеют графики, если система имеет три решения?
Как записывается решение системы уравнений, если она решается графическим способом?
От чего зависит количество решений системы уравнений при графическом способе?
Сколько точек пересечения имеют графики, если система имеет три решения?
Слайд 6Графический способ
построить графики уравнений в одной координатной плоскости;
найти координаты точек
пересечения графиков, которые и будут решением системы
Слайд 13Cпособ подстановки
Как решить систему способом подстановки?
Есть ли разница, из какого
уравнения системы получить подстановку?
Как записать решение системы?
Как записать решение системы?
Слайд 14Cпособ подстановки
Выражают из какого-нибудь уравнения системы одну переменную через другую;
Подставляют
в другое уравнение системы вместо этой переменной полученное выражение;
Решают полученное уравнение с одной переменной;
Находят соответствующее значение второй переменной, из подстановки.
Решают полученное уравнение с одной переменной;
Находят соответствующее значение второй переменной, из подстановки.
Слайд 20Способ сложения
Умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при
одной из переменных стали противоположные числа;
Складывают почленно левые и правые части уравнений системы;
Решают получившееся уравнение с одной переменной;
Находят соответствующее значение второй переменной.
Складывают почленно левые и правые части уравнений системы;
Решают получившееся уравнение с одной переменной;
Находят соответствующее значение второй переменной.