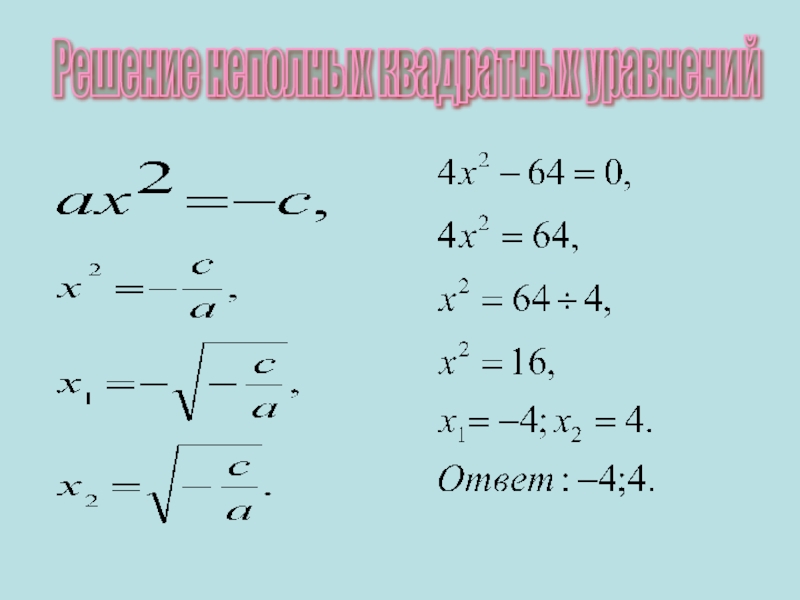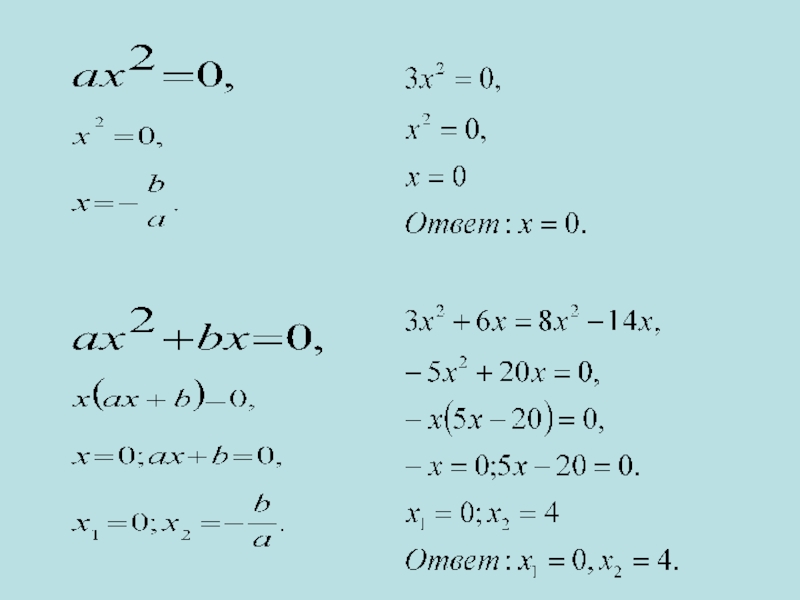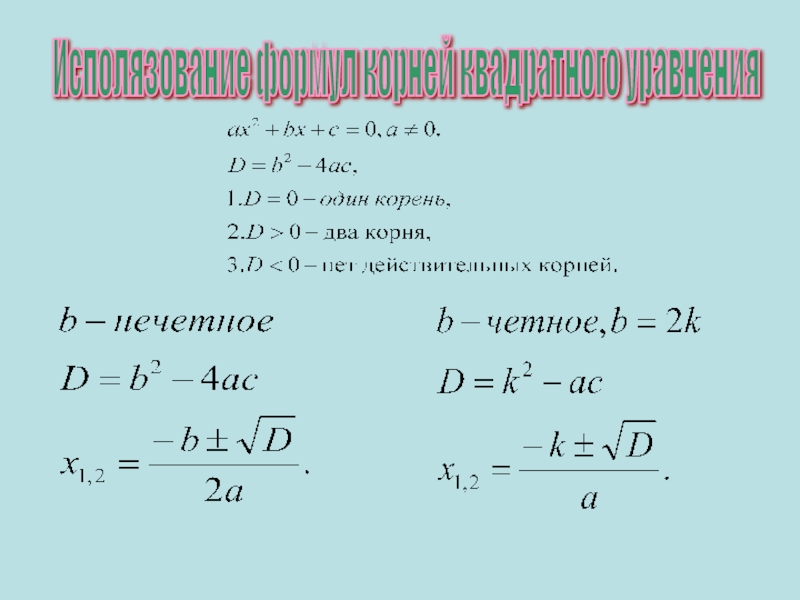решения
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку на тему Квадратные уравнения
Содержание
- 1. Презентация к уроку на тему Квадратные уравнения
- 2. вопросы...Определение квадратного уравненияВиды квадратных уравненийРешение квадратных уравнений
- 3. Уравнение вида
- 4. виды квадратных уравненийполные квадратные уравнениянеполные квадратные уравненияприведенное квадратное уравнение
- 5. Решение неполных квадратных уравнений
- 6. Слайд 6
- 7. Способы решения квадратных уравнений Разложение
- 8. Разложение левой части на множители
- 9. Метод выделения полного квадрата
- 10. Исполязование формул корней квадратного уравнения
- 11. примеры
- 12. Применение теоремы Виета
- 13. Введение новой переменнойУравнение видас последующим решениемЯвляется уравнением,
- 14. По сумме коэффициентов квадратного уравнения
- 15. Графический способ- Графиком функции является парабола- Графиком
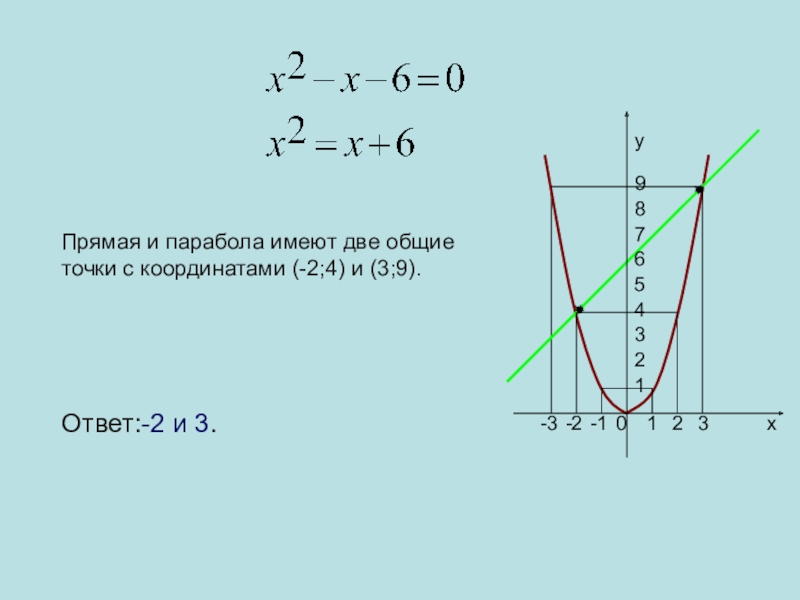
- 16. 0123-1-2-3123456789xyПрямая и парабола имеют две общие точки с координатами (-2;4) и (3;9).Ответ:-2 и 3.
- 17. 0123-1-2-3123456789xyПрямая и парабола имеют одну общую точку с координатами (2;4).Ответ: 2.
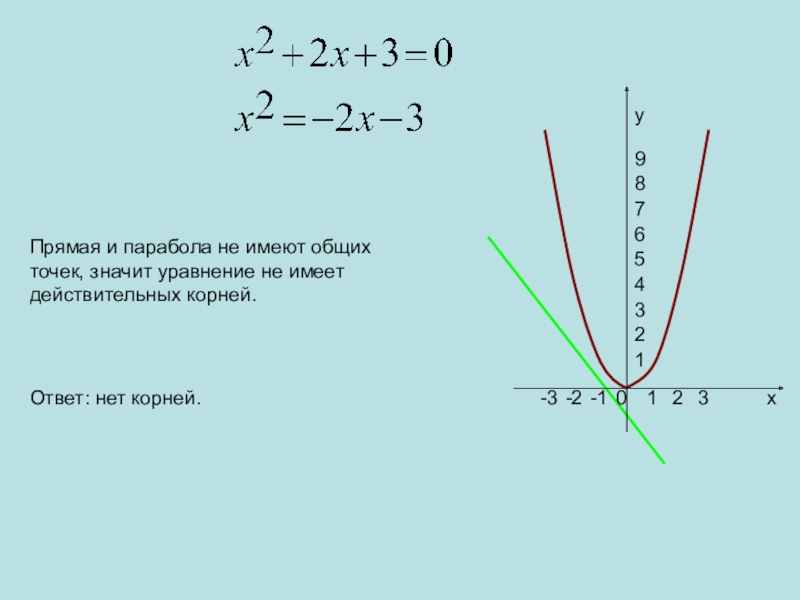
- 18. 0123-1-2-3123456789xyПрямая и парабола не имеют общих точек, значит уравнение не имеет действительных корней.Ответ: нет корней.
- 19. ВыводУ нас хорошие знания, поэтому мы можем
вопросы...Определение квадратного уравненияВиды квадратных уравненийРешение квадратных уравнений
Слайд 1квадратные уравнения
Выполнили: Баранов Антон, Чаннов Алексей
Учитель: Климова С.Н.
Виды квадратных уравнений
и способы
Слайд 2вопросы...
Определение квадратного уравнения
Виды квадратных уравнений
Решение квадратных уравнений
Слайд 3Уравнение вида
,
где -переменная,
- некоторые числа,
, называется квадратным уравнением.
Примеры:
Примеры:
Слайд 4виды квадратных уравнений
полные
квадратные
уравнения
неполные
квадратные
уравнения
приведенное квадратное уравнение
Слайд 7Способы решения
квадратных уравнений
Разложение левой части на множители;
Метод
выделения полного квадрата;
Применение формул корней квадратного уравнения;
Применение теоремы Виета;
Введение новой переменной;
По сумме коэффициентов квадратного уравнения;
Графический.
Применение формул корней квадратного уравнения;
Применение теоремы Виета;
Введение новой переменной;
По сумме коэффициентов квадратного уравнения;
Графический.
Слайд 13Введение новой переменной
Уравнение вида
с последующим решением
Является уравнением, сводящимся к квадратному.
квадратного
уравнения
Если ,
то уравнение принимает вид
Такое уравнение называется биквадратным.
В общем случае оно решается заменой
Слайд 15Графический способ
- Графиком функции является парабола
- Графиком функции является прямая
Прямая
и парабола имеют только одну общую точку, значит уравнение имеет одно решение;
Прямая и парабола имеют две общие точки, абсциссы этих точек являются корнями квадратного уравнения;
Прямая и парабола не имеют общих точек, значит уравнение не имеет корней.
Прямая и парабола имеют две общие точки, абсциссы этих точек являются корнями квадратного уравнения;
Прямая и парабола не имеют общих точек, значит уравнение не имеет корней.
Слайд 16
0
1
2
3
-1
-2
-3
1
2
3
4
5
6
7
8
9
x
y
Прямая и парабола имеют две общие точки с координатами (-2;4) и
(3;9).
Ответ:-2 и 3.
Ответ:-2 и 3.
Слайд 17
0
1
2
3
-1
-2
-3
1
2
3
4
5
6
7
8
9
x
y
Прямая и парабола имеют одну общую точку с координатами (2;4).
Ответ: 2.
Слайд 18
0
1
2
3
-1
-2
-3
1
2
3
4
5
6
7
8
9
x
y
Прямая и парабола не имеют общих точек, значит уравнение не имеет
действительных корней.
Ответ: нет корней.
Ответ: нет корней.
Слайд 19Вывод
У нас хорошие знания, поэтому мы можем решить любое квадратное уравнение.
Мы знаем разные способы решения и можем их применять на практике. Учитесь и вам все будет по силам! Хорошие знания это билет в светлое будущее!