идёшь за кем-то вслед,
Дорога не запомнится.
Зато, куда б ты ни попал
И по какой распутице
Дорога та, что сам искал,
Вовек не позабудется.
Н.Рыленков
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики в 11 классе при подготовке к ЕГЭ по теме Задание В12
Содержание
- 1. Презентация к уроку математики в 11 классе при подготовке к ЕГЭ по теме Задание В12
- 2. По заданиям ЕГЭ 14Исследование
- 3. Предмет исследования:
- 4. Актуальность исследования:Необходимость сдачи ЕГЭ по математике.Источники исследований:Открытый банк к задачам ЕГЭ по математике.
- 5. Особенности экзаменационных
- 6. Типы заданий:Исследование степенных ,показательных функций;Исследование произведения показательной
- 7. Производные элементарных функций;Правила дифференцирования;Монотонность и экстремумы функции;Наибольшее и наименьшее значения функции.Это надо знать.
- 8. Признак максимума (минимума). Если функция f(x) – непрерывна в точке х0
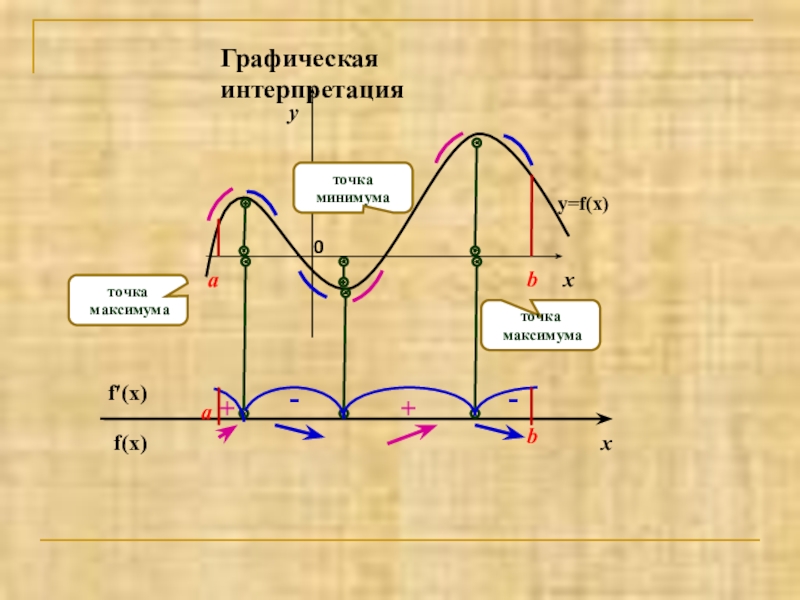
- 9. xyaby=f(x)точка максимуматочка максимуматочкаминимумаf(x)f′(x)ab++--0xГрафическая интерпретация
- 10. ОДЗ у(х)Производная у’(х)Уравнение у’(х) = 0На числовой
- 11. Найдите точку минимума функции№ 124315ОДЗ у(х)Производная у’(х)Уравнение
- 12. Пробуйте, возможно решение проще, записав функцию y
- 13. Найдите точку минимума функции Ответ: -17
- 14. [o; π/2]Найдите наименьшее значение функциина отрезке№ 77499ОДЗ
- 15. Найдите наибольшее
- 16. //////////////////////////////////////Найдите точку минимума функции№ 282860Найдите наименьшее значение
- 17. 3cos²x− 3Y’ = =3(1-cos²x)cos²x≥ 0очевидноФункция возрастаетНаибольшее на
- 18. Найдите наибольшее значение функции № 245180tФункция y
- 19. Задание В14 решаем без производной. Найдите наибольшее значение функцииНайдите наибольшее значение функции
- 20. 1.Найдите наибольшее значение функции у=(8-х)ех-7 на промежутке
- 21. Из анализа заданий банка ЕГЭ и бланка
- 22. Найти наибольшее (наименьшее)значение функции на отрезкеНайти точку
- 23. Найдите точку минимума функции№ 132061Найдите точку максимума
- 24. Найдите наибольшее значение функции№ 245184Найдите наибольшее значение
- 25. сегодня я узнал…было интересно…было трудно…я выполнял задания…я
По заданиям ЕГЭ 14Исследование функции с помощью производной Подготовила учитель математики МБОУ-СОШ №8Сербинович Елена Владимировна
Слайд 2По заданиям ЕГЭ 14
Исследование функции с помощью производной
Подготовила учитель математики
МБОУ-СОШ №8
Сербинович Елена Владимировна
Слайд 3 Предмет исследования:
задания В14.
Цель:
разобрать, классифицировать задания В14.
Задачи исследования:
Найти оптимальные способы решения;
Выработать рекомендации к решению различных типов задач В14.
Слайд 4Актуальность исследования:
Необходимость сдачи ЕГЭ по математике.
Источники исследований:
Открытый банк к задачам ЕГЭ
по математике.
Слайд 5Особенности экзаменационных
заданий В 14.
Задания В14 представляют собой следующие задачи :
Нахождение точек экстремума;
Нахождение экстремумов функции;
Нахождение наибольших и наименьших значений функции.
Следует обратить внимание на различия в понятиях точка экстремума, координаты точки экстремума, наибольшее и наименьшее значение функции.
Слайд 6Типы заданий:
Исследование степенных ,показательных функций;
Исследование произведения показательной функции на многочлен;
Исследование частного
двух многочленов;
Исследование функций, содержащих логарифмы;
Исследование тригонометрических функций;
Способы решения:
- с помощью производной;
- без производной (по свойствам функции)
Исследование функций, содержащих логарифмы;
Исследование тригонометрических функций;
Способы решения:
- с помощью производной;
- без производной (по свойствам функции)
Слайд 7Производные элементарных функций;
Правила дифференцирования;
Монотонность и экстремумы функции;
Наибольшее и наименьшее значения функции.
Это
надо знать.
Слайд 9x
y
a
b
y=f(x)
точка
максимума
точка
максимума
точка
минимума
f(x)
f′(x)
a
b
+
+
-
-
0
x
Графическая интерпретация
Слайд 10
ОДЗ у(х)
Производная у’(х)
Уравнение у’(х) = 0
На числовой прямой Х
Общий алгоритм решения:
Значения
функции
на концах отрезка
и в точках отрезка
на концах отрезка
и в точках отрезка
ИЛИ
с помощью
производной
(правила и действия
дифференцирования)
- знаки производной
- монотонность
- точка экстремума
- наибольшее (наименьшее)
значение функции
без производной
Исследование функции
2
Аналогичное будет на ЕГЭ
Слайд 11
Найдите точку минимума функции
№ 124315
ОДЗ у(х)
Производная у’(х)
Уравнение у’(х) = 0
(- ∞;
+ ∞)
y’(x) =
3
x²
- 192
= 0
|
:
3
3
X =
X₂ =
- 8
8
На числовой прямой Х
- 8
8
(х – 8)
(х + 8)
к методу интервалов
//////////////
//////////
///////////////////////
знаки у’(х)
+
+
–
монотонность у(х)
8 – ответ
Общий алгоритм решения:
х
3
₁
•
•
Слайд 12Пробуйте, возможно решение проще, записав функцию y = 3x – 3ln(x+3)
Ещё
раз…
/////////////
////////
////////
////////////
Найдите наименьшее значение функции
на отрезке
№ 26714
ОДЗ у(х)
Производная у’(х)
Уравнение у’(х) = 0
На числовой прямой Х
Общий алгоритм решения:
(х + 3)³
> 0
→
х + 3
> 0,
х
> - 3
-3
3 –
1
(х + 3)³
∙
((х + 3)³)’
=
3 –
(х + 3)³
3(х + 3)²
=
3 –
х + 3
3
=
0
3 –
х + 3
3
х + 3
– 3
=
0
3(х + 3)
х + 3
=
0
3(х + 2)
-3
-2
методом интервалов
знаки у’(х)
+
+
–
y(- 2) =
- 6
Х = -2
Х ≠ -3
11
Слайд 14
[o; π/2]
Найдите наименьшее значение функции
на отрезке
№ 77499
ОДЗ у(х)
Производная у’(х)
Уравнение у’(х) =
0
На числовой прямой Х
Общий алгоритм решения:
(- ∞; + ∞)
y’(x) =
5
2
5
−
cos x
= 0
: 5
→
= 0
→
cos x
cos x
=
выбор Х на отрезке
[o; π/2]
На единичной окружности
•
•
0
π/2
•
•
π/4
У(0) =
У(π/4) =
У(π/2) =
3-5π/4
- 2
3 + 5π/4 – 5√2
наименьшее
ответ
С тригонометрическими функциями …
[o; π/2]
С
’
= 0
12
![[o; π/2]Найдите наименьшее значение функциина отрезке№ 77499ОДЗ у(х)Производная у’(х)Уравнение у’(х) = 0На числовой прямой ХОбщий алгоритм решения:(-](/img/thumbs/79a1f8a30f857e1b55f3182677d7c59a-800x.jpg "Презентация к уроку математики в 11 классе при подготовке к ЕГЭ по теме Задание В12 [o; π/2]Найдите наименьшее значение функциина отрезке№ 77499ОДЗ у(х)Производная у’(х)Уравнение у’(х) =")
Слайд 15
Найдите наибольшее значение функции
Ответ: 16
на
отрезке [-4;4]
Стационарная точка х=-1
Критическая точка х=-5
У(-1)=16-наибольшее
![Найдите наибольшее значение функции Ответ: 16на отрезке [-4;4]Стационарная точка х=-1Критическая точка х=-5У(-1)=16-наибольшее](/img/thumbs/ccb499c6c147dcd84d79d23f004c5080-800x.jpg "Презентация к уроку математики в 11 классе при подготовке к ЕГЭ по теме Задание В12 Найдите наибольшее значение функции Ответ: 16на отрезке [-4;4]Стационарная точка х=-1Критическая точка х=-5У(-1)=16-наибольшее")
Слайд 16
///////////
///////////
////////////////
Найдите точку минимума функции
№ 282860
Найдите наименьшее значение функции
на отрезке
№ 282861
у ’=
((х + 3)²)’
(х + 5)
- 1’ =
+ (х + 3)²
(х + 5)’
= 1 ∙ 2(х + 3)
(х + 5)
+ (х + 3)² =
= 2(х² + 8х + 15)
+ (х² + 6х + 9)
у’ = 3х² + 22х + 39
ОДЗ
(-∞; +∞)
Производная
у ’=
3х² + 22х + 39
Уравнение у ’ = 0
Х₁ =
Х₂ =
−3
K № 282860
х
•
•
(схематически парабола)
Знаки у ’
+
+
−
монотонность
функции
−3
Х = -3
Значения функции
на концах отрезка
и точках отрезка:
производная произведения
(f(kx + b))’ = kf’(kx + b)
K № 282861
Производная функции
(действия и правила дифференцирования)
На числовой прямой Х
y(-4) =
y(-1) =
y(-3) =
0
15
−1
Подставим
Иначе:
на отрезке [-4;-1]
y(-3) =
−1
Сравните условия и задание. Алгоритмы решения. Приёмы решения.
5
1. Находим у ’
2. Решаем у ’= 0,
Х = -3
Є
[-4; -1]
На числовой прямой Х
Парабола у ’
монотонность
функции
Отрезок [-4;-1]
-4
-1
///////////
////////////////
х
•
•
+
−
−3
Знаки у ’
•
•
Слайд 173
cos²x
− 3
Y’ =
=
3(1-cos²x)
cos²x
≥ 0
очевидно
Функция возрастает
Наибольшее на [-5π/6; 0] Y(0)=5
Найдите
наибольшее значение функции
на отрезке
на отрезке
Найдите наибольшее значение функции
на отрезке
Обратите внимание
16
![3cos²x− 3Y’ = =3(1-cos²x)cos²x≥ 0очевидноФункция возрастаетНаибольшее на [-5π/6; 0] Y(0)=5Найдите наибольшее значение функции](/img/thumbs/93d0a43be8047716f86e78aff2529a56-800x.jpg "Презентация к уроку математики в 11 классе при подготовке к ЕГЭ по теме Задание В12 3cos²x− 3Y’ = =3(1-cos²x)cos²x≥ 0очевидноФункция возрастаетНаибольшее на [-5π/6; 0] Y(0)=5Найдите наибольшее")
Слайд 18
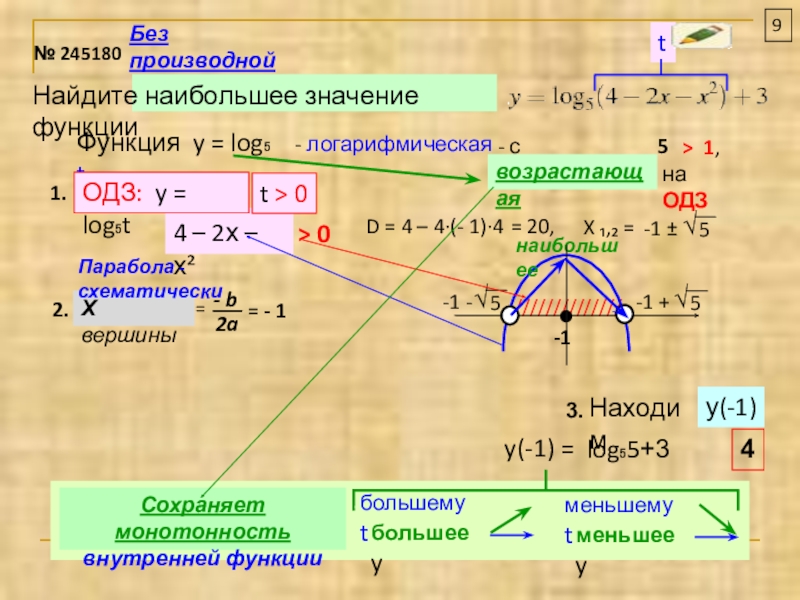
Найдите наибольшее значение функции
№ 245180
t
Функция y = log₅ t
- логарифмическая
,
- с основанием
5
> 1,
возрастающая
на ОДЗ
D = 4 – 4∙(- 1)∙4
= 20,
X ₁‚₂ =
-1 ±
5
4 – 2х – х²
> 0
ОДЗ: y = log₅t
t > 0
1.
///////////////
наибольшее
Х вершины
=
- b
2a
= - 1
•
-1
2.
Парабола - схематически
большему t
большее y
меньшему t
меньшее y
Находим
у(-1)
4
y(-1) =
3.
Сохраняет монотонность
внутренней функции
log₅5+3
9
Без производной
Слайд 19Задание В14 решаем без производной.
Найдите наибольшее значение функции
Найдите
наибольшее значение функции
Слайд 20
1.Найдите наибольшее значение функции у=(8-х)ех-7 на промежутке 3≤х≤10.
2.Найдите наименьшее значение функции
у=(х2-8х+8)е2-х на промежутке 1≤х≤7.
3.Найдите наибольшее значение функции у=Ln(Х+5) -5Х на промежутке -4,5≤х≤0.
4.Найдите наименьшее значение функции у=3х- Ln(Х+3) на промежутке -2,2≤х≤0.
3.Найдите наибольшее значение функции у=Ln(Х+5) -5Х на промежутке -4,5≤х≤0.
4.Найдите наименьшее значение функции у=3х- Ln(Х+3) на промежутке -2,2≤х≤0.
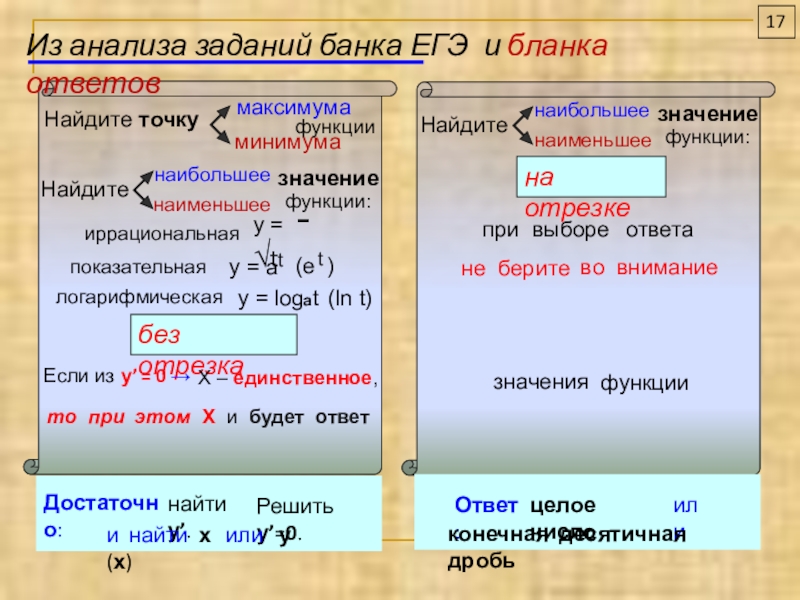
Слайд 21
Из анализа заданий банка ЕГЭ и бланка ответов
Найдите
точку
максимума
минимума
Найдите
наибольшее
наименьшее
значение
функции:
функции
иррациональная
показательная
логарифмическая
y = logat
(ln
t)
без отрезка
Если из y’ = 0
Х – единственное,
то при этом Х и будет ответ
→
Достаточно:
найти у’.
Решить у’=0.
и найти х или у(х)
17
Найдите
наибольшее
наименьшее
значение
функции:
на отрезке
при выборе
ответа
не берите
во внимание
для сравнения
«Не вычисляемые»
значения
функции
Ответ:
целое число
или
конечная десятичная дробь
Слайд 22Найти наибольшее (наименьшее)
значение функции на отрезке
Найти точку максимума (минимума)
функции
1)
Найдите производную функции
2)
Решите
уравнение f’ (x) = 0
3)
Выбрать корни уравнения f’ (x) = 0,
принадлежащие данному отрезку
3)
Корни уравнения f’ (x) = 0 из ОДЗ
нанести на числовую прямую
4)
Найти значения функции на концах
отрезка и в точках, принадлежащих ему
4)
Установить знак производной на
на каждом промежутке, подставив
число из промежутка ↓
то есть монотонность функции на
на каждом промежутке
5)
Выбрать ответ по условию задания
Алгоритм – памятка ко всем В 14
18
Решаем
Слайд 23Найдите точку минимума функции
№ 132061
Найдите точку максимума функции
№ 130971
Найдите наибольшее значение
функции
на отрезке
на отрезке
№ 130849
Найдите наибольшее значение функции
на отрезке
№ 130119
Найдите наибольшее значение функции
на отрезке .
№ 129809
Найдите точку минимума функции
№ 124315
Найдите точку минимума функции
№ 128209
Найдите точку максимума функции
№ 127905
1
2
3
4
5
6
7
8
̌
̌
20
минизадачник
̌
̌
Слайд 24Найдите наибольшее значение функции
№ 245184
Найдите наибольшее значение функции
№ 245176
Найдите наименьшее значение
функции
на отрезке
на отрезке
№ 77499
Найдите точку максимума функции
№ 77500
Найдите наименьшее значение функции
на отрезке
№ 77495
Найдите точку минимума функции
принадлежащую промежутку
№ 77493
Найдите наибольшее значение функции
на отрезке .
№ 77481
Найдите наименьшее значение функции
на отрезке
№ 26714
Найдите наименьшее значение функции
на отрезке
№ 77425
Найдите точку минимума функции
№ 77459
̌
9
10
11
12
13
14
15
16
17
18
̌
̌
21
̌
Слайд 25сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я
почувствовал, что…
я научился…
меня удивило…
мне захотелось…
я научился…
меня удивило…
мне захотелось…
