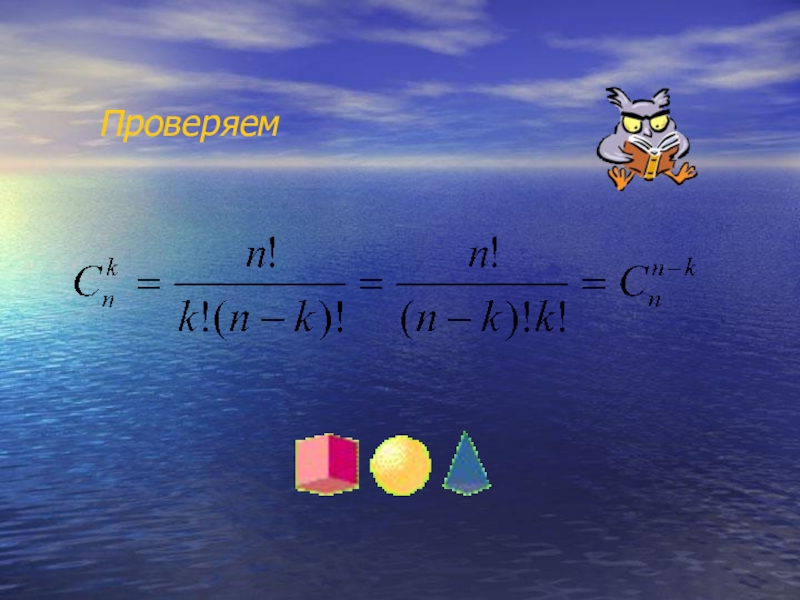- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики Сочетания (11 класс)
Содержание
- 1. Презентация к уроку математики Сочетания (11 класс)
- 2. Цели урока:образовательная обучать решению задач по комбинаторикеразвивающая
- 3. Задачи урока: дать определение сочетания, основные формулыпоказать
- 4. Объяснение нового материала Сочетанием из данных
- 5. Число сочетаний из n элементов по k
- 6. Для любого k количество размещений из nэлементов
- 7. Пример. Сколькими различными способами из семи
- 8. Докажем справедливость формул (4)
- 9. Докажем формулу (3), что и требовалось доказать.
- 10. Доказать формулу (4) самостоятельно
- 11. Проверяем
- 12. Замечание. Выше числа определялись для
- 13. Проверка усвоения материала1. Повторяем «факториал»1. Вычислите:а) 6!
Слайд 2Цели урока:
образовательная
обучать решению задач по комбинаторике
развивающая
развивать логическое мышление
расширять математический
развивать навыки научно-исследовательской деятельности
воспитательная
воспитывать культуру письма, речи
развивать умения работать в группе
формировать чувство ответственности за принятое решение
Слайд 3Задачи урока:
дать определение сочетания, основные формулы
показать способы решения задач
отработать умения
проверить понимание материала, изученного на уроках
Слайд 4 Объяснение нового материала Сочетанием из данных n элементов по k называют любую
Например, из трех элементов x1, x2, x3 можно составить следующие сочетания по два элемента:
x1, x2,; x1, x3 ; x2, x3
Других сочетаний из рассматриваемых трех элементов по 2 нет.
Приведем сочетания из четырех элементов по 3: x1, x2, x3 ,x4
x1, x2, x3; x1, x2, x4;
x1, x3, x4; x2, x3, x4.
Подчеркнем, что понятие сочетания не связано с расположением (порядком) элементов. Если в данном сочетании переставить каким-либо образом его элементы, то оно (как сочетание) не изменится.
Слайд 5
Число сочетаний из n элементов по k обозначают
(от фр. Combination –
Вычисляя число размещений, мы получили пары, отличающиеся порядком элементов, например x1, x2 и x2, x1 . Из двух элементов можно составить две перестановки, т. е. P2 упорядоченных пар, поэтому так как число размещений равно количеству групп - , умноженному на число перестановок внутри группы P2
Слайд 6
Для любого k количество размещений из n
элементов по k можно вычислить
(1)
Действительно, из n элементов можно составить групп по k элементов, а в каждой группе можно выполнить Pk перестановок. Таким образом, число всех размещений равно произведению числа групп и числа перестановок внутри этих групп Pk , т. е. справедлива формула (1). Следовательно,
(2)
Слайд 7
Пример. Сколькими различными способами из семи участников математического кружка можно
Так как порядок, в котором будут выбраны два
человека, безразличен, то число
равновозможных случаев составить команду
равно
Слайд 12Замечание. Выше числа определялись для k≥1
Иногда удобно рассматривать число
При k=0 формула (2) не имеет смысла, но формула (3) имеет смысл. В самом деле, так как считается, что 0! = 1, то
Но тогда при k = 0 имеют смысл также и формулы (4) и (5):
Поэтому в дальнейшем при использовании чисел будем пользоваться формулой (3), считая, что 0≤k≤n.
Слайд 13Проверка усвоения материала
1. Повторяем «факториал»
1. Вычислите:
а) 6! + 7!; б)
2. Сократите дробь .
3. Решите уравнение если n є N:
(2n – 3)! = 23(2n – 4)!.
2. Упражнения на использование формулы (3)
Найдите:
а) ; б) ; в) ; г) ; д) ; е) .