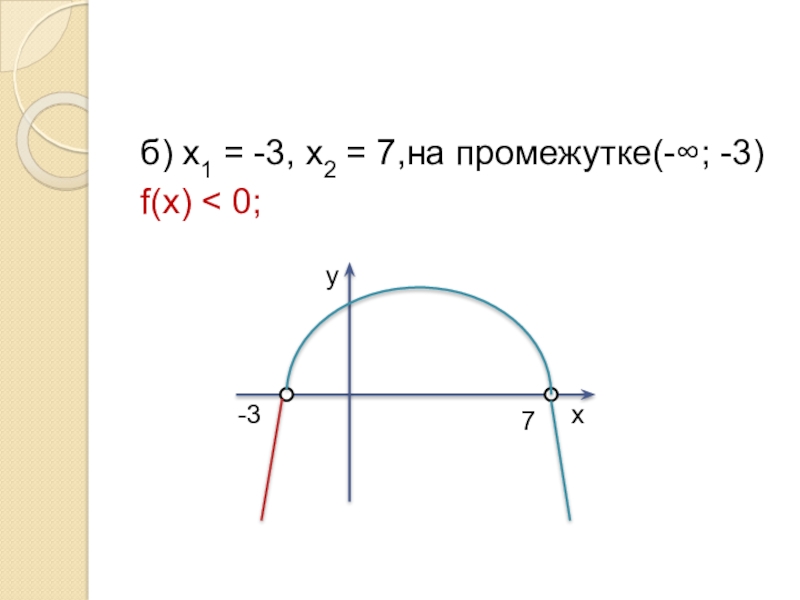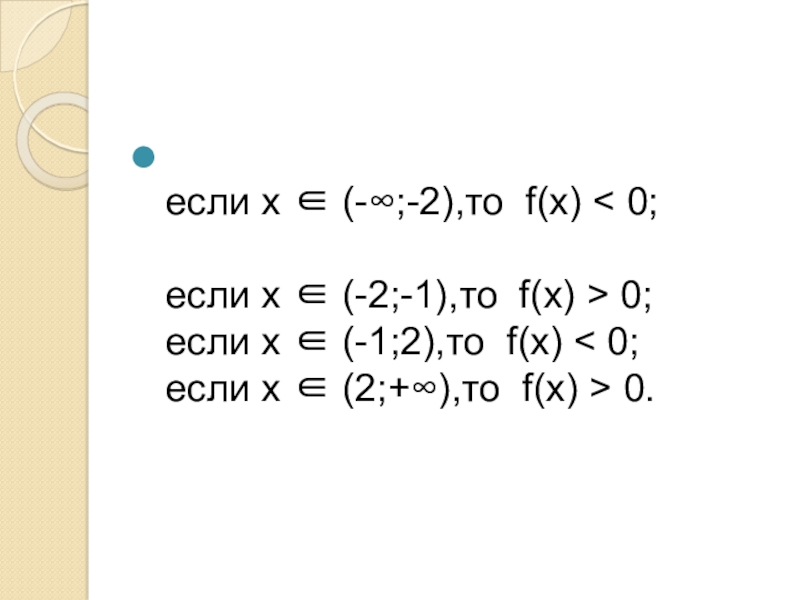ты славой,
О, светоч всех земных светил!
Тебя царицей величавой
Недаром Гаусс окрестил.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики по теме: Решение неравенств методом интервалов (9 класс)
Содержание
- 1. Презентация к уроку математики по теме: Решение неравенств методом интервалов (9 класс)
- 2. Устная работа
- 3. 1. Разложите на множители выражение:а) 169 -
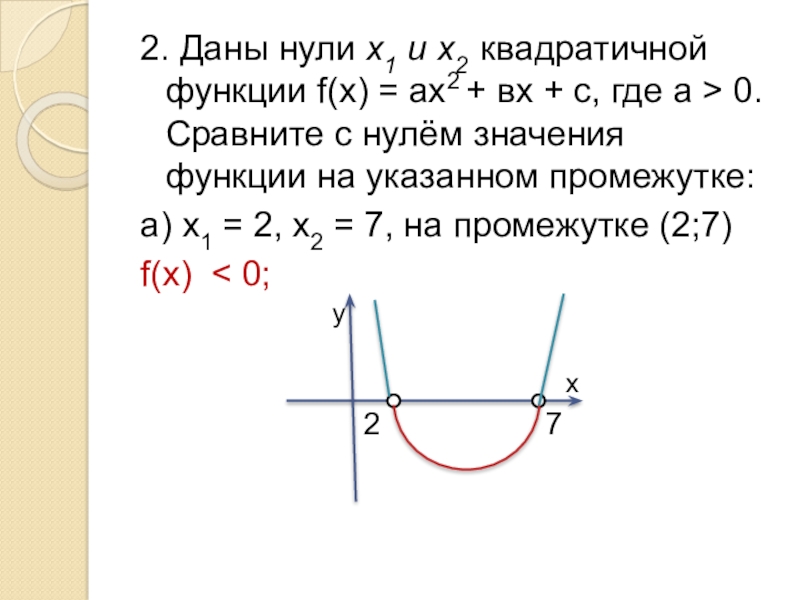
- 4. 2. Даны нули х1 и х2 квадратичной
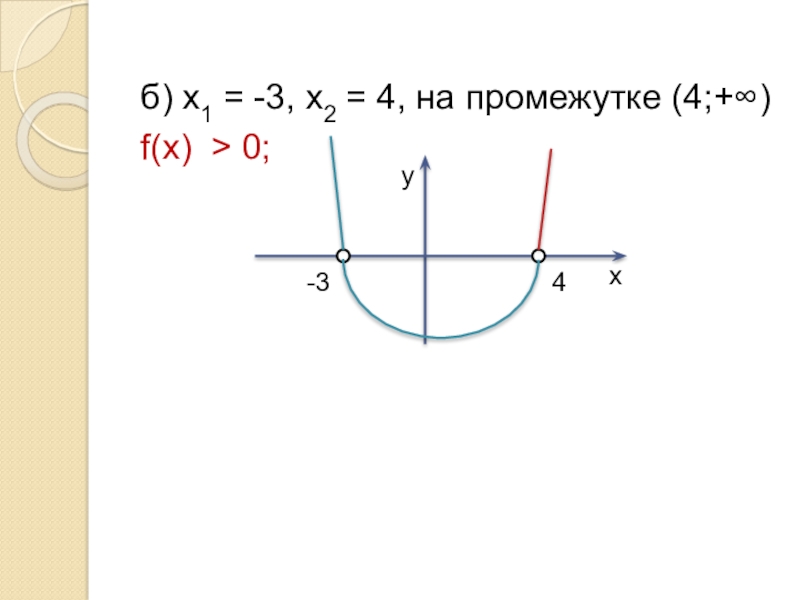
- 5. б) х1 = -3, х2 = 4, на промежутке (4;+∞) f(х) > 0; х-34у
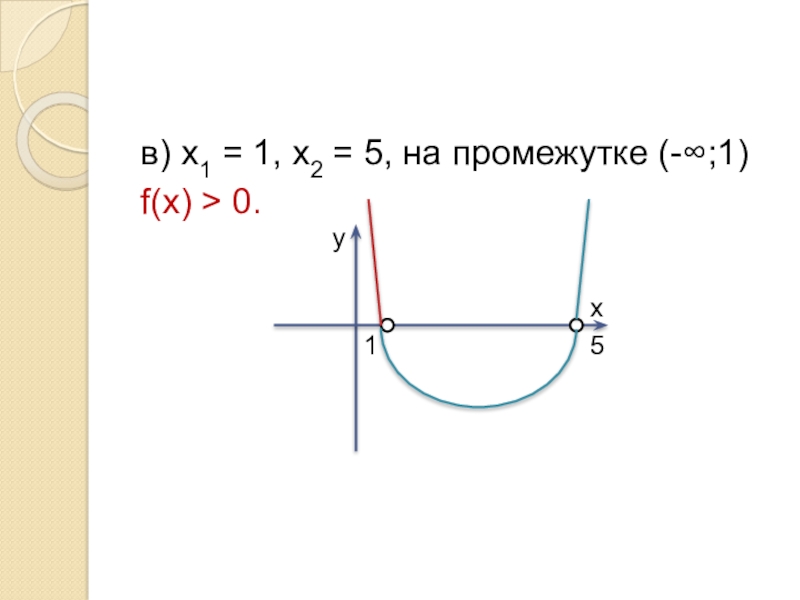
- 6. в) х1 = 1, х2 = 5, на промежутке (-∞;1) f(х) > 0.51ух
- 7. Слайд 7
- 8. б) х1 = -3, х2 = 7,на промежутке(-∞; -3) f(х) < 0;ух-3 7
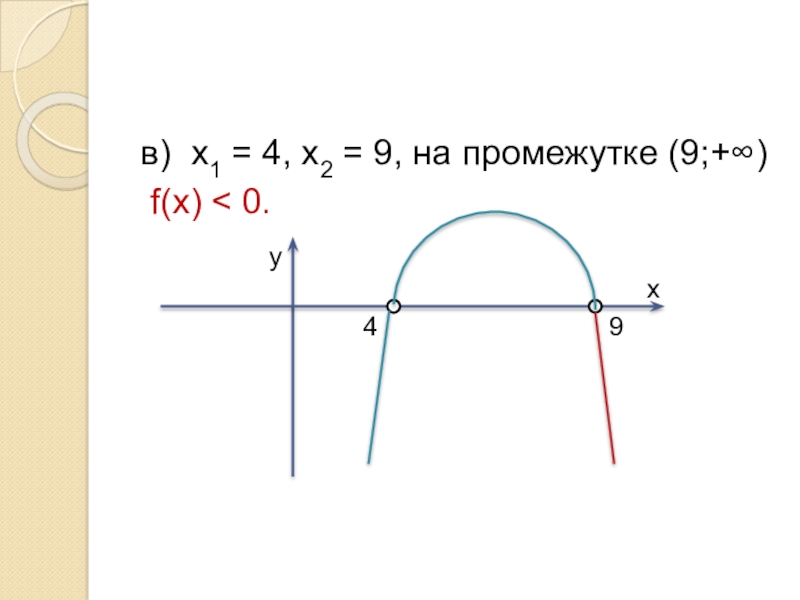
- 9. в) х1 = 4, х2 = 9, на промежутке (9;+∞) f(х) < 0.49ух
- 10. Решите неравенство:(х2 – 4) (х + 1)>0.
- 11. (х2 – 4) (х + 1) (х – 7) > 0.Решите неравенство:
- 12. Тема урока: «Решение целых рациональных неравенств методом интервалов»
- 13. понятие
- 14. Решить неравенство методом интервалов (х2 – 4) (х + 1)>0
- 15. Найдите область определения этой функции;Назовите нули функции;Отметьте
- 16. f(х) = (х+2)(х-2)(х+1).D(f)=R.f(х)=0 при х=-2 или х=2
- 17. если х ∈ (-∞;-2),то f(х) < 0;
- 18. если х ∈ (-∞;-2),то f(х) <
- 19. Слайд 19
Устная работа
Слайд 1О, математика, ты вечна! Гордись, прекрасная собой! Твоё величье бесконечно, Так предначертано судьбой. Всегда овеяна
Слайд 31. Разложите на множители выражение:
а) 169 - а2;
г) в2 + 10в + 9;
б) х2 - 2; д) -х2 + 8х;
в) у3 + 1; е) х2 + 16х + 64.
б) х2 - 2; д) -х2 + 8х;
в) у3 + 1; е) х2 + 16х + 64.
Слайд 42. Даны нули х1 и х2 квадратичной функции f(х) = ах2
+ вх + с, где а > 0. Сравните с нулём значения функции на указанном промежутке:
а) х1 = 2, х2 = 7, на промежутке (2;7)
f(х) < 0;
а) х1 = 2, х2 = 7, на промежутке (2;7)
f(х) < 0;
2
7
у
х
Слайд 7
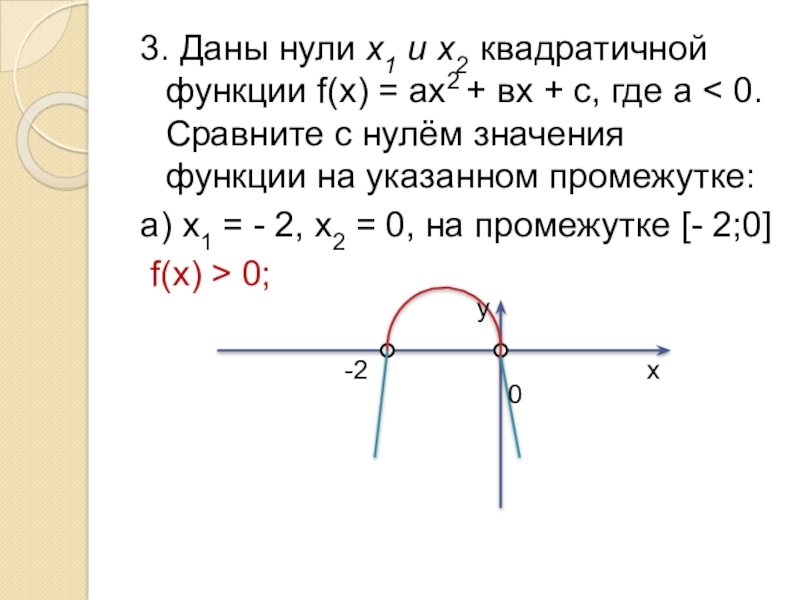
3. Даны нули х1 и х2 квадратичной функции f(х) = ах2 + вх + с, где а < 0. Сравните с нулём значения функции на указанном промежутке:
а) х1 = - 2, х2 = 0, на промежутке [- 2;0]
f(х) > 0;
0
-2
у
х
Слайд 13 понятие неравенства второй
степени с одной переменной и
методы их решения.
применять метод интервалов при
решении неравенств с одной
переменной, дробных
рациональных неравенств.
Знать:
Уметь:
Слайд 15Найдите область определения этой функции;
Назовите нули функции;
Отметьте их на координатном луче.
Что они сделали с областью определения?
Изобразите интервалы.
Выясните, каковы знаки функции в каждом из указанных промежутков.
Выберите промежуток, соответствующий знаку неравенства ( «+» – знак >, « – » – знак <)
Изобразите интервалы.
Выясните, каковы знаки функции в каждом из указанных промежутков.
Выберите промежуток, соответствующий знаку неравенства ( «+» – знак >, « – » – знак <)
План решения неравенства :
Слайд 16f(х) = (х+2)(х-2)(х+1).
D(f)=R.
f(х)=0 при х=-2 или х=2 или х=-1.
Ответ: х ∈
( -2; -1 ) ∪ ( 2; +∞ )
Решение неравенства:
Текст надписи
-2
-1
2
-
-
+
+
Слайд 18 если х ∈ (-∞;-2),то f(х) < 0; если х ∈ (-2;-1),то f(х)
> 0;
если х ∈ (-1;2),то f(х) < 0;
если х ∈ (2;+∞),то f(х) > 0.
