- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики на тему Способы решения квадратных уравнений
Содержание
- 1. Презентация к уроку математики на тему Способы решения квадратных уравнений
- 2. 1. Дайте определение квадратного уравнения.2. Виды квадратных уравнений.3. Теорема Виета.Повторение пройденного материала
- 3. Способы решения квадратных уравнений
- 4. х2 + 2х = 0х2 – 81
- 5. Определить вид квадратного уравнения и назвать способы
- 6. Рассмотрим квадратное уравнение ах2 + вх +
- 7. Решить уравнение: 2х2 -11х + 15 =
- 8. Теорема: если сумма коэффициентов квадратного уравнения ах2
- 9. Решить уравнение: 11х2 + 25х – 36
- 10. Это старый и
- 11. Примеры.1. Для уравненияz2 – 9z + 8
- 12. Для уравненияz2 + 5z - 6 =
- 13. Для уравненияz2 + 4z + 3 =
- 14. Решите с помощью номограммы уравнения:I вариантz2 -
- 15. Если в уравнениих2 + рх
- 16. Определить по рисунку, сколько корней имеет
- 17. Определить, сколько корней имеет квадратное уравнение (обосновать):Х2 - 2х + 1 = 0.Назовите корни этого уравнения.
- 18. Определить, сколько корней имеет квадратное уравнение (обосновать):Х2 - 2х + 5 = 0.Назовите корни этого уравнения.
- 19. IX способ: Решение квадратных уравнений с помощью
- 20. Схема построения: 1) Построим центр окружности S(
- 21. ПРИ ЭТОМ ВОЗМОЖНЫ ТРИ СЛУЧАЯ.1) Радиус окружности
- 22. НАЗОВИТЕ КОРНИ УРАВНЕНИЯ ПО ПРЕДЛОЖЕННОМУ РИСУНКУ.1) х2 – 2х – 3 = 0х
- 23. Назовите корни уравнения по предложенному рисунку.2) х2 + 4х + 4 = 0
- 24. Назовите корни уравнения по предложенному рисунку.3) х2 – 2х + 3 = 0
- 25. X способ: Геометрический способ решения квадратных уравнений
- 26. Площадь S квадрата ABCD можно представить как
- 27. Перечислите способы решения квадратных уравнений.Рефлексия
- 28. Решить с помощью циркуля и линейки квадратные
- 29. Всем спасибо за урок!
Слайд 21. Дайте определение квадратного уравнения.
2. Виды квадратных уравнений.
3. Теорема Виета.
Повторение пройденного
Слайд 4х2 + 2х = 0
х2 – 81 = 0
Определить вид квадратного
I способ:
разложение левой части уравнения на множители.
Слайд 5Определить вид квадратного уравнения и назвать способы его решения
Х2 + 6х
I I способ:
метод выделения полного квадрата
I I I способ:
решение квадратных уравнений по формулам
I V способ:
с использованием теоремы Виета (прямой и обратной)
Слайд 6Рассмотрим квадратное уравнение ах2 + вх + с =0, где коэффициент
у2 +ву +ас = 0, равносильному данному. Его корни найдем с помощью теоремы Виета. Окончательно получаем х1 = у1 /а, х2 = у2 /а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому способ и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета, и когда дискриминант есть точный квадрат.
V способ:
«переброска» коэффициентов
Слайд 7Решить уравнение: 2х2 -11х + 15 = 0.
Решение:
Коэффициент а=2 умножим на
у2 – 11у + 30 = 0, где х = у/2
2. По теореме Виета получаем: у1=5, у2=6.
3. Х1=5/2=2,5 х2=6/2=3.
Ответ. х1 =2,5; х2 = 3.
Самостоятельно решить уравнение:
I вариант: 4х2 + 12х + 5 = 0
IIвариант: 6х2 + 5х – 6 = 0
V способ:
«переброска» коэффициентов
Ответ.
I вариант: х = -0,5; х = -2,5 I I вариант: х = 2/3; х = -1,5
Слайд 8Теорема:
если сумма коэффициентов квадратного уравнения
ах2 + вх + с
х1 =1,
х2 =с/а.
VI способ:
Свойства коэффициентов квадратного уравнения
Слайд 9Решить уравнение: 11х2 + 25х – 36 = 0.
Решение:
Применим теорему
11+25+(-36)=0, значит х1 =1, х2 =-36/11.
Ответ. х1 =1, х2 =-36/11.
Устно решить уравнения:
а) 5х2 -7х+2=0
б) 3х2 +5х-8=0
Слайд 10 Это старый и незаслуженно забытый способ решения
( таблица XXII, способ описан на стр.83).
Номограмма для решения уравнения z2+pz+q=0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Решение квадратных уравнений с помощью номограммы
V I I способ:
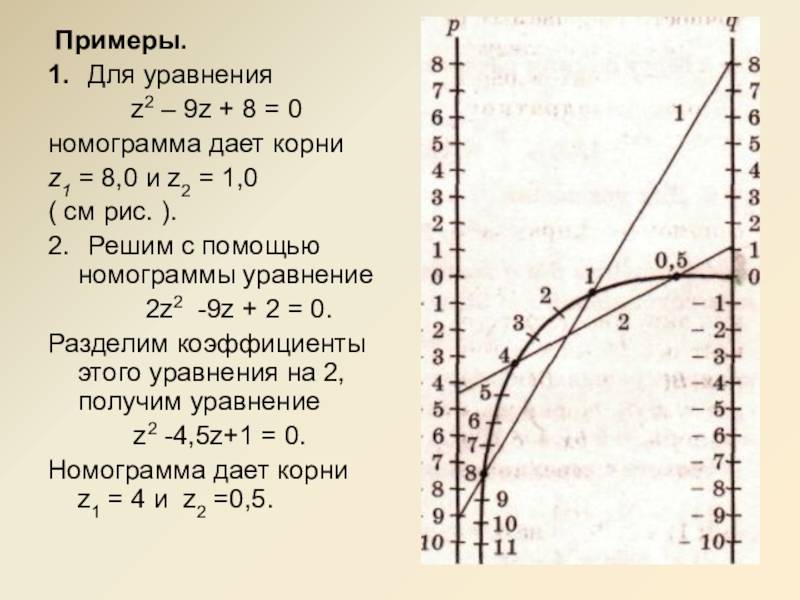
Слайд 11 Примеры.
1. Для уравнения
z2 – 9z + 8 = 0
номограмма дает корни
z1 = 8,0 и z2 = 1,0
( см рис. ).
2. Решим с помощью номограммы уравнение
2z2 -9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z2 -4,5z+1 = 0.
Номограмма дает корни z1 = 4 и z2 =0,5.
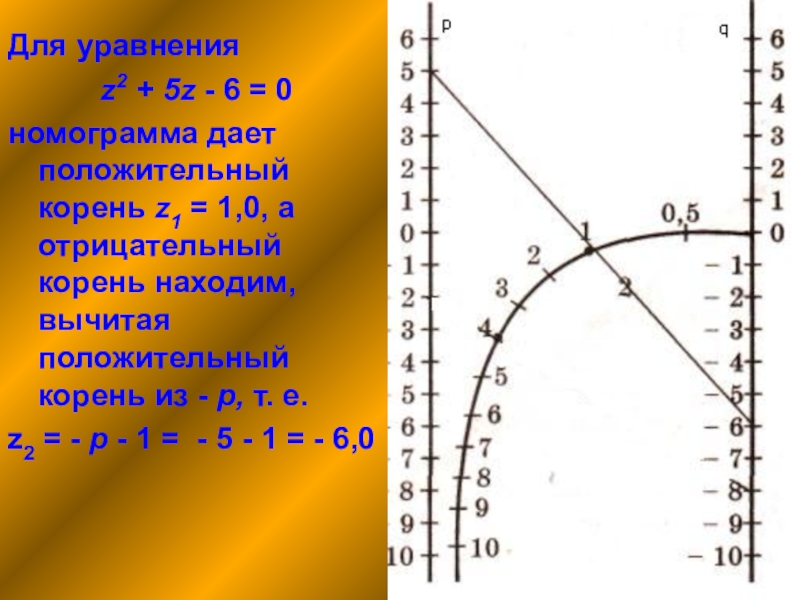
Слайд 12Для уравнения
z2 + 5z - 6 = 0
номограмма дает положительный корень
z2 = - р - 1 = - 5 - 1 = - 6,0
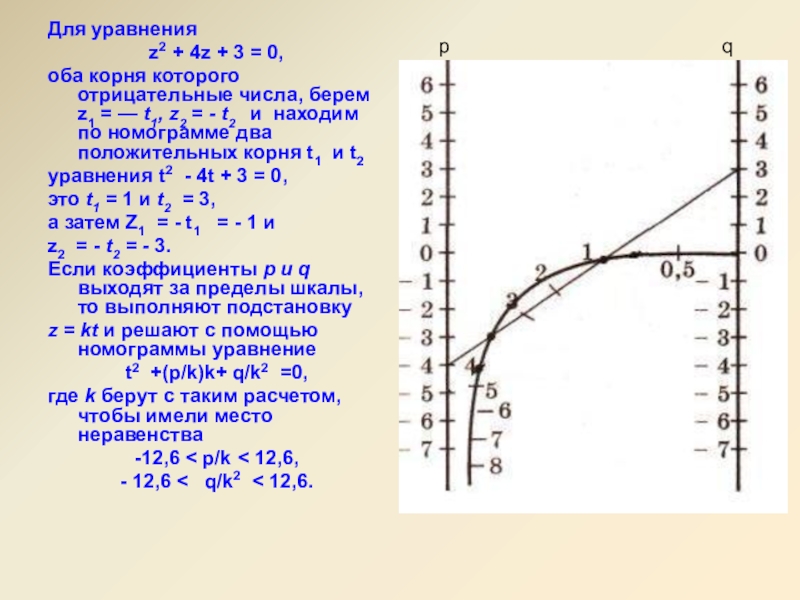
Слайд 13Для уравнения
z2 + 4z + 3 = 0,
оба корня которого отрицательные
уравнения t2 - 4t + 3 = 0,
это t1 = 1 и t2 = 3,
а затем Z1 = - t1 = - 1 и
z2 = - t2 = - 3.
Если коэффициенты р и q выходят за пределы шкалы, то выполняют подстановку
z = kt и решают с помощью номограммы уравнение
t2 +(p/k)k+ q/k2 =0,
где k берут с таким расчетом, чтобы имели место неравенства
-12,6 < p/k < 12,6,
- 12,6 < q/k2 < 12,6.
p
q
Слайд 14Решите с помощью номограммы уравнения:
I вариант
z2 - 4z + 4 =
z2 –z – 6 = 0
z2 + 5z + 4 = 0
II вариант
z2 - 7z + 6 = 0
z2 + 4z - 5 = 0
z2 + 5z + 6 = 0
Ответ.
a) z1 =3,5; z2 =1,0
b) z1 =3; z2 = -2
c) z1 = -4; z2 = -1
Ответ.
a) z1 =6,5; z2 =1,5
b) z1 =1; z2 = -5
c) z1 = -3; z2 = -2
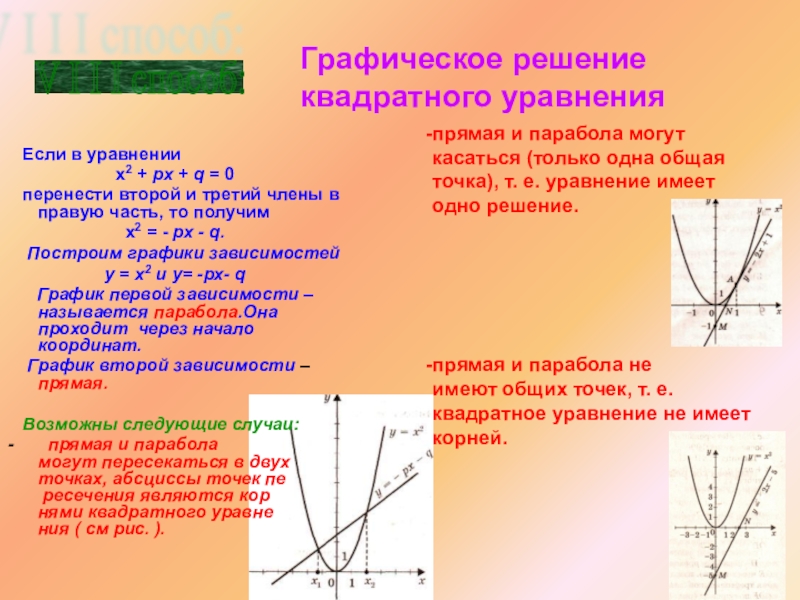
Слайд 15 Если в уравнении
х2 + рх + q = 0
х2 = - рх - q.
Построим графики зависимостей
у = х2 и у= -рх- q
График первой зависимости – называется парабола.Она проходит через начало координат.
График второй зависимости – прямая.
Возможны следующие случаи:
- прямая и парабола могут пересекаться в двух точках, абсциссы точек пе ресечения являются кор нями квадратного уравне ния ( см рис. ).
V I I I способ:
Графическое решение квадратного уравнения
прямая и парабола могут касаться (только одна общая точка), т. е. уравнение имеет одно решение.
прямая и парабола не
имеют общих точек, т. е.
квадратное уравнение не имеет корней.
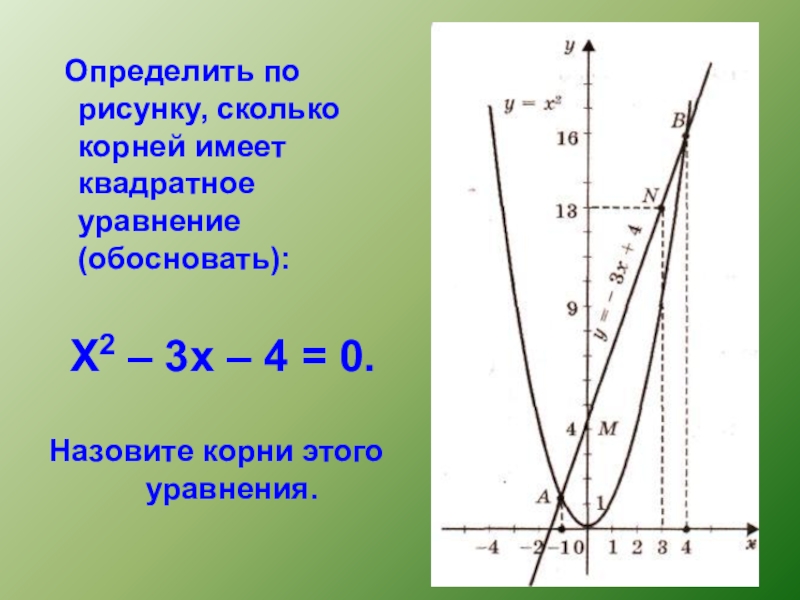
Слайд 16 Определить по рисунку, сколько корней имеет квадратное уравнение (обосновать):
Х2
Назовите корни этого уравнения.
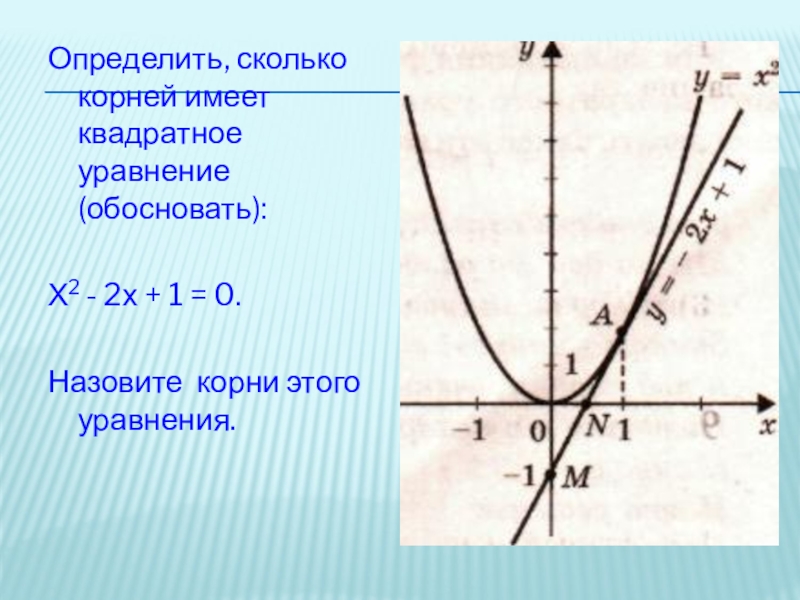
Слайд 17Определить, сколько корней имеет квадратное уравнение (обосновать):
Х2 - 2х + 1
Назовите корни этого уравнения.
Слайд 18
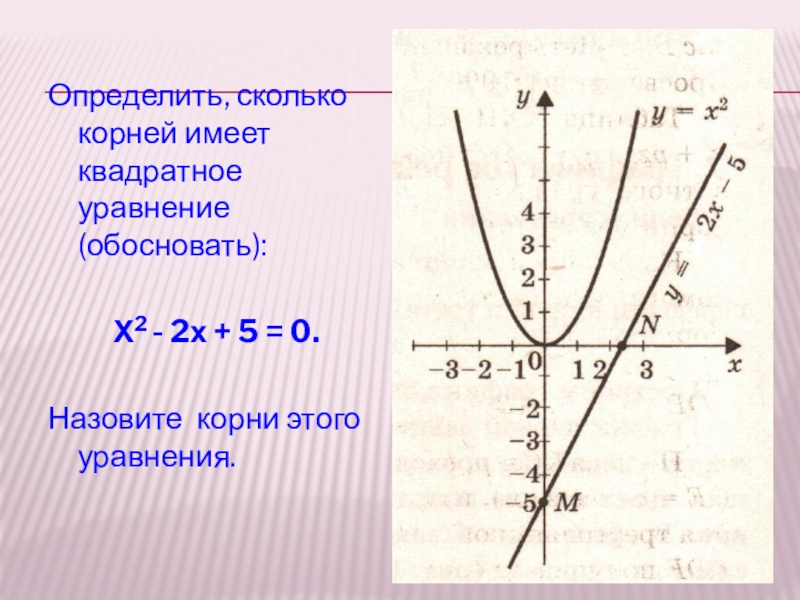
Определить, сколько корней имеет квадратное уравнение (обосновать):
Х2 - 2х + 5
Назовите корни этого уравнения.
Слайд 19IX способ:
Решение квадратных уравнений с помощью циркуля и линейки
Графический способ
ах2 + bх + с = 0 c помощью циркуля и линейки.
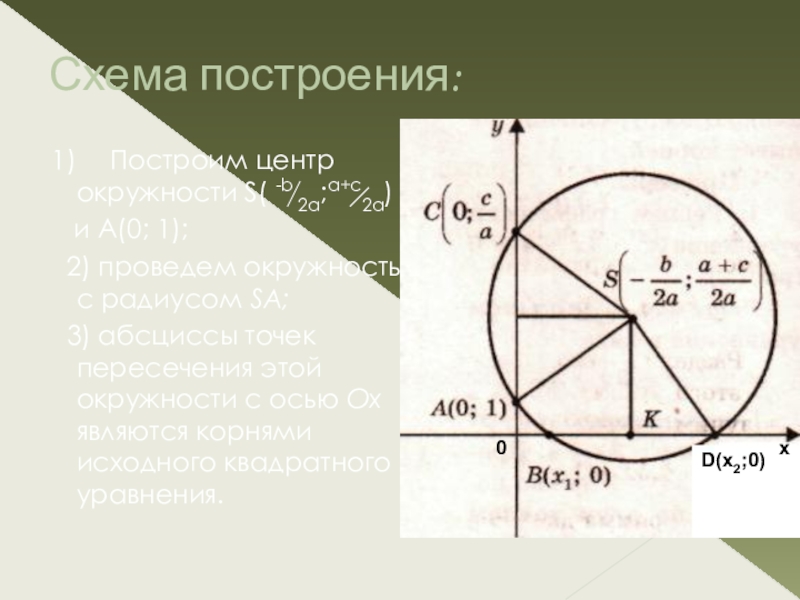
Слайд 20Схема построения:
1) Построим центр окружности S( -b 2a;а+с2а)
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
D(х2;0)
х
0
Слайд 21ПРИ ЭТОМ ВОЗМОЖНЫ ТРИ СЛУЧАЯ.
1) Радиус окружности больше ординаты центра:
окружность пересекает
2) Радиус окружности равен ординате центра
окружность касается оси Ох, т.е. уравнение имеет 2 равных корня
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью Ох, т.е. уравнение не имеет корней.
Слайд 25X способ:
Геометрический способ решения квадратных уравнений
В древности,
Примеры.
1. Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим
образом:
«Квадрат и десять корней равны 39» (рис.).
Решение.
Рассмотрим квадрат со стороной х, на его сторонах
строятся прямоугольники так, что другая сторона каждого
из них равна 212, следовательно, площадь каждого
равна 21 2 х. Полученную фигуру дополняют затем до
нового квадрата ABCD, достраивая в углах четыре равных
квадрата, сторона каждого из них 21 2 , а площадь 61 4 .
х
х
х2
212х
21 2х
212х
212х
614
614
614
614
D
C
B
A
Слайд 26Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата
и четырех пристроенных квадратов (614*4=25), т.е. S= х2 + 10х + 25.
Заменяя х2 + 10 числом 39, получим, что
S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т. е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
Х = 8 – 212 – 212 = 3.
Слайд 28
Решить с помощью циркуля и линейки квадратные уравнения:
1) х2 –
2) х2 + 4х + 4 = 0
3) х2 – 2х + 3 = 0
4) х2 – 5х + 4 = 0
Домашнее задание.