- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики Функции
Содержание
- 1. Презентация к уроку математики Функции
- 2. Две взаимно перпендикулярные числовые оси с общим
- 3. Координатная плоскость делится осями на четыре части,
- 4. Функция может быть задана с помощью ее
- 5. Линейная функцияЛинейной называется функция вида у =
- 6. Квадратичной функцией называется функция вида Графиком квадратичной
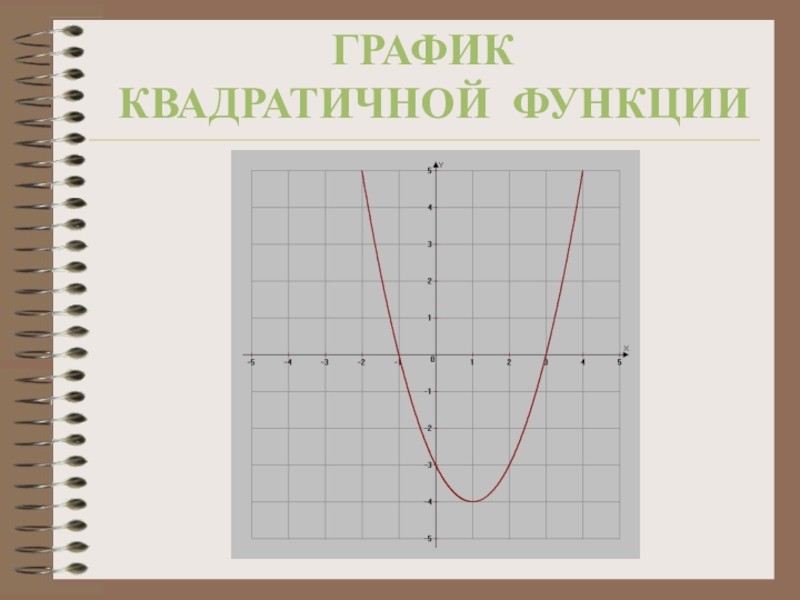
- 7. ГрафикКвадратичной функции
- 8. Кубическая функцияГрафик функции — кубическая параболаСоставим таблицу
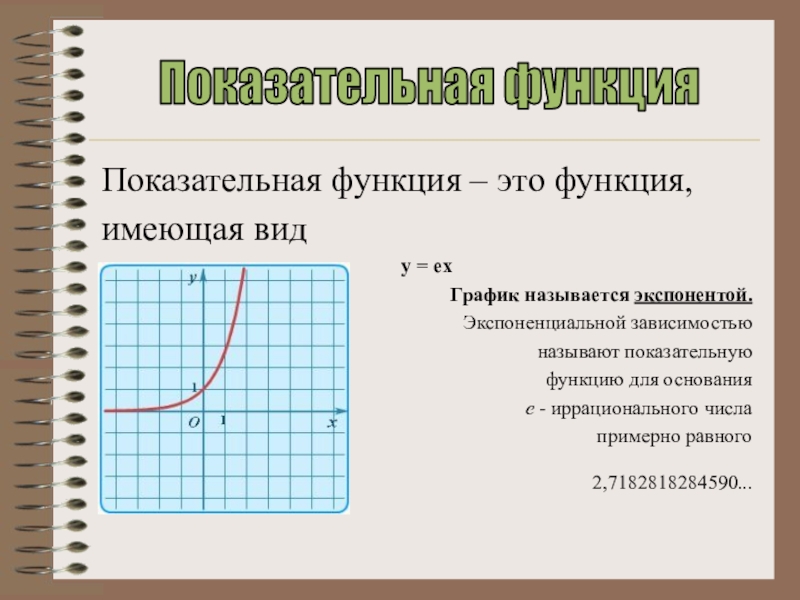
- 9. Показательная функция – это функция,имеющая вид y
- 10. Это функция вида y = lnx или y =
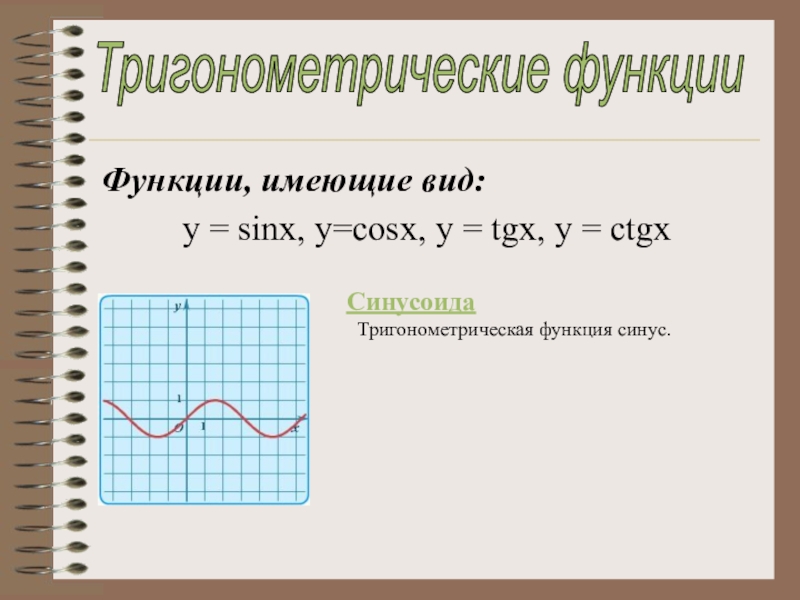
- 11. Функции, имеющие вид: y = sinx, y=cosx, y
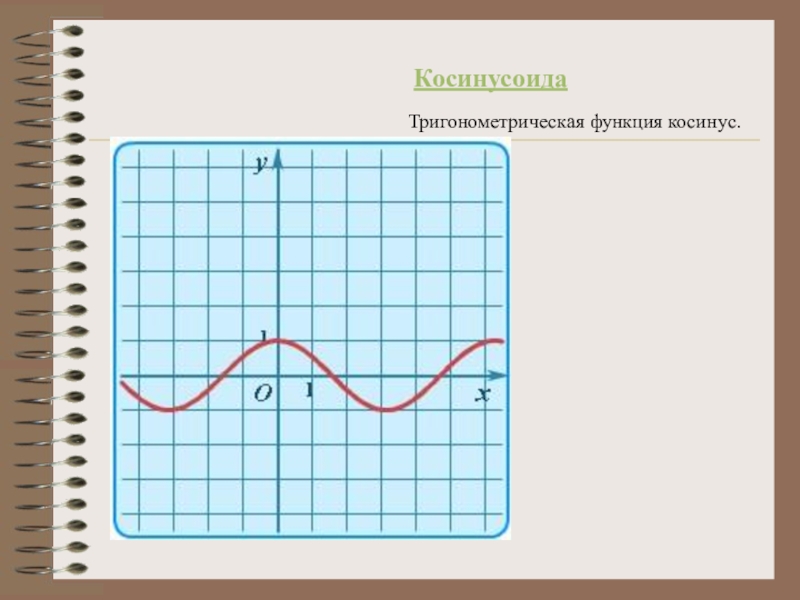
- 12. Тригонометрическая функция косинус. Косинусоида
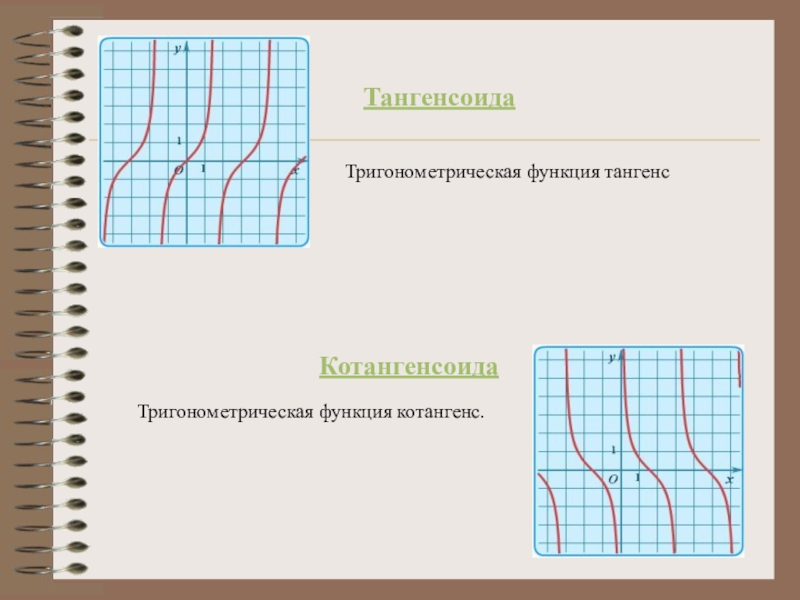
- 13. Тангенсоида Тригонометрическая функция тангенс Тригонометрическая функция котангенс. Котангенсоида
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
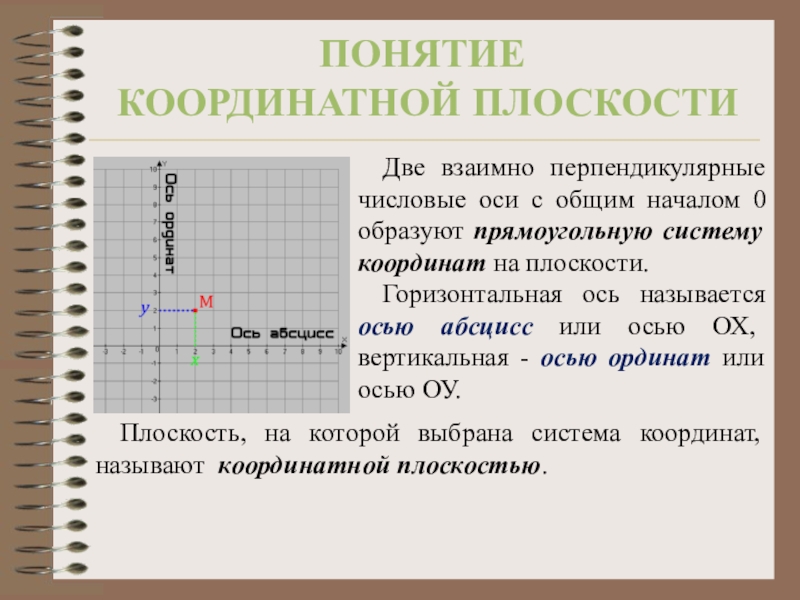
Слайд 2Две взаимно перпендикулярные числовые оси с общим началом 0 образуют прямоугольную
Горизонтальная ось называется осью абсцисс или осью ОХ, вертикальная - осью ординат или осью ОУ.
Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Понятие
координатной плоскости
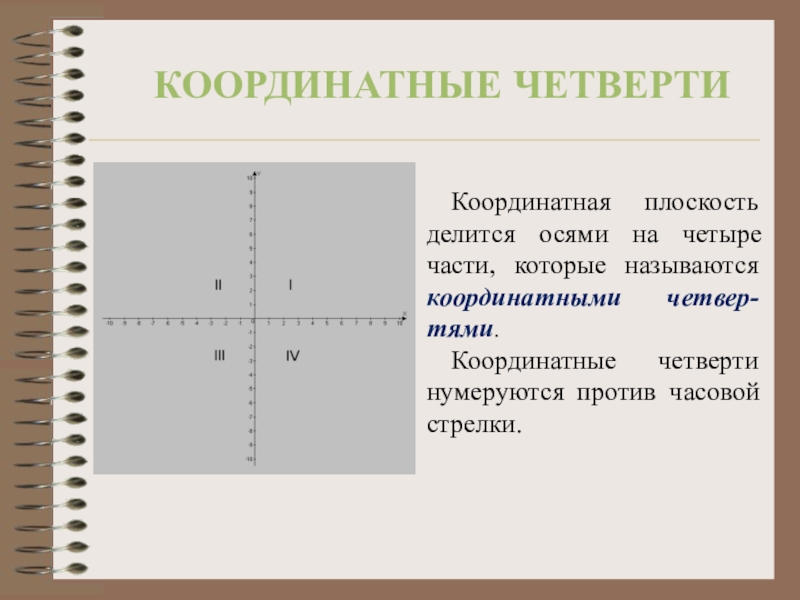
Слайд 3Координатная плоскость делится осями на четыре части, которые называются координатными четвер-тями.
Координатные
координатные четверти
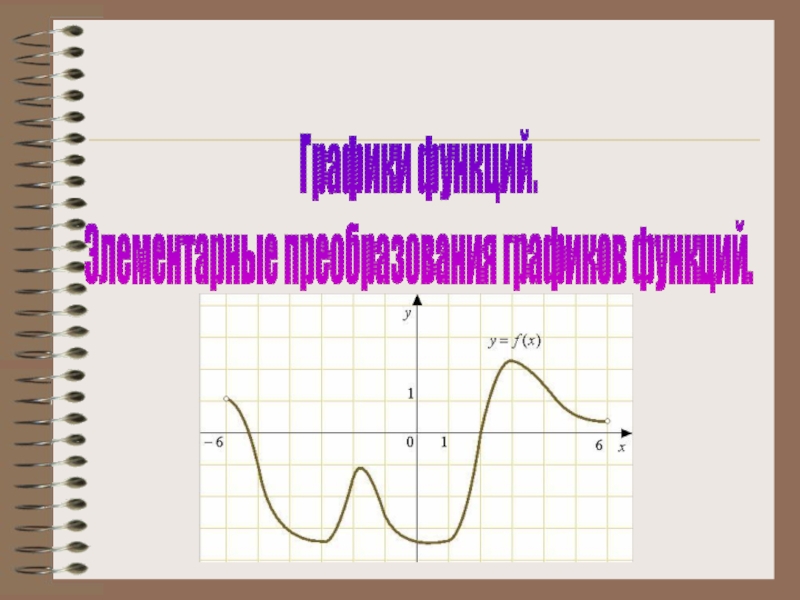
Слайд 4Функция может быть задана с помощью ее графика.
На координатной плоскости 0ХУ
Графический способ
Задания функции
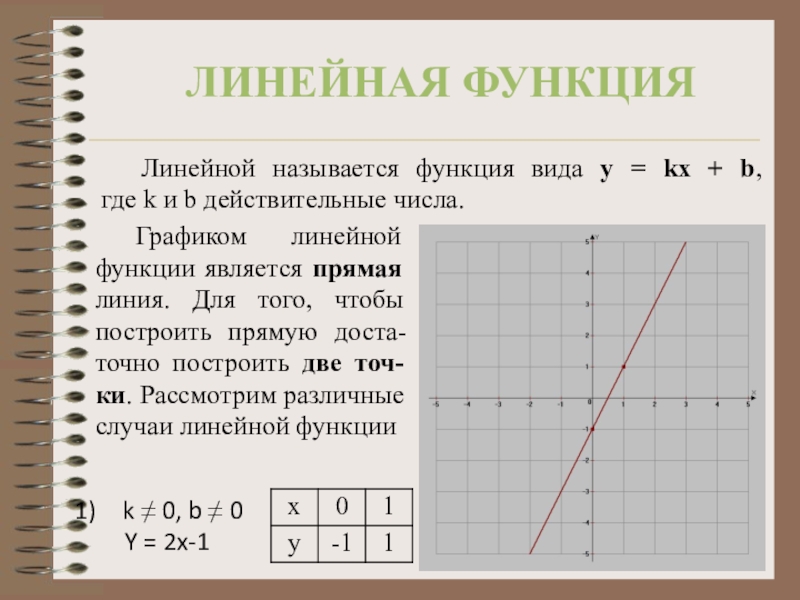
Слайд 5Линейная функция
Линейной называется функция вида у = kх + b,
где
k 0, b 0
Y = 2x-1
Графиком линейной функции является прямая линия. Для того, чтобы построить прямую доста-точно построить две точ-ки. Рассмотрим различные случаи линейной функции
Слайд 6Квадратичной функцией называется функция вида
Графиком квадратичной функции является парабола. Алгоритм
Направление ветвей параболы:
При a > 0 — ветви параболы направлены вверх.
При a < 0 — ветви параболы направлены вниз.
Квадратичная функция
Слайд 8Кубическая функция
График функции — кубическая парабола
Составим таблицу значения функции в 5-ти
Свойства функции y=x3
Область определения: множество всех действительных чисел
Множество значений: множество всех действительных чисел
Функция нечетная
Нули функции: y=0 при x=0
Функция возрастает на всей области определения
Слайд 9Показательная функция – это функция,
имеющая вид
y = ex
График называется экспонентой.
Экспоненциальной зависимостью
называют показательную
функцию для основания
e - иррационального числа
примерно равного
2,7182818284590...
Показательная функция
Слайд 10Это функция вида
y = lnx или y = logа x
Логарифмическая функция
График
Слайд 11Функции, имеющие вид:
y = sinx, y=cosx, y = tgx, y =
Тригонометрические функции
Синусоида
Тригонометрическая функция синус.