- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Квадратичная функция. 9 класс.
Содержание
- 1. Презентация к уроку Квадратичная функция. 9 класс.
- 2. Определение квадратичной функции Функцию, которую можно задать формулой
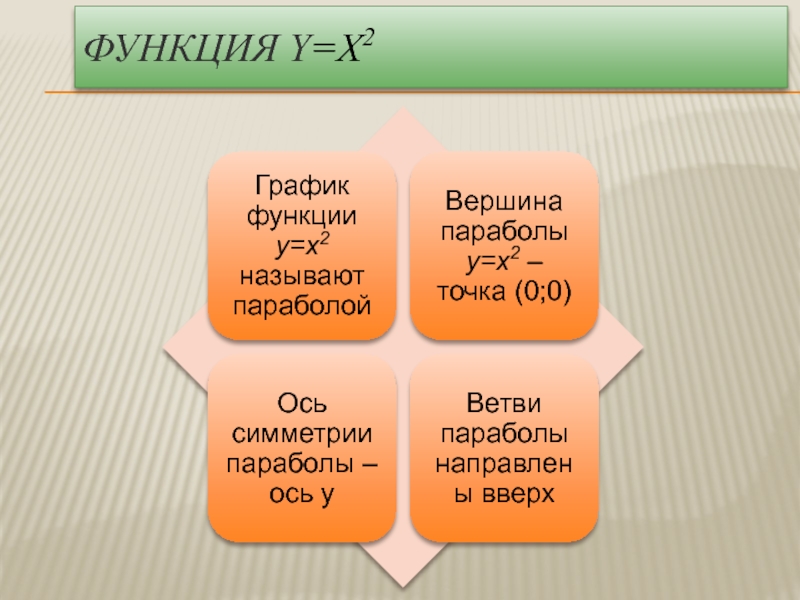
- 3. Функция Y=x2
- 4. Слайд 4
- 5. Свойства функции y = x2
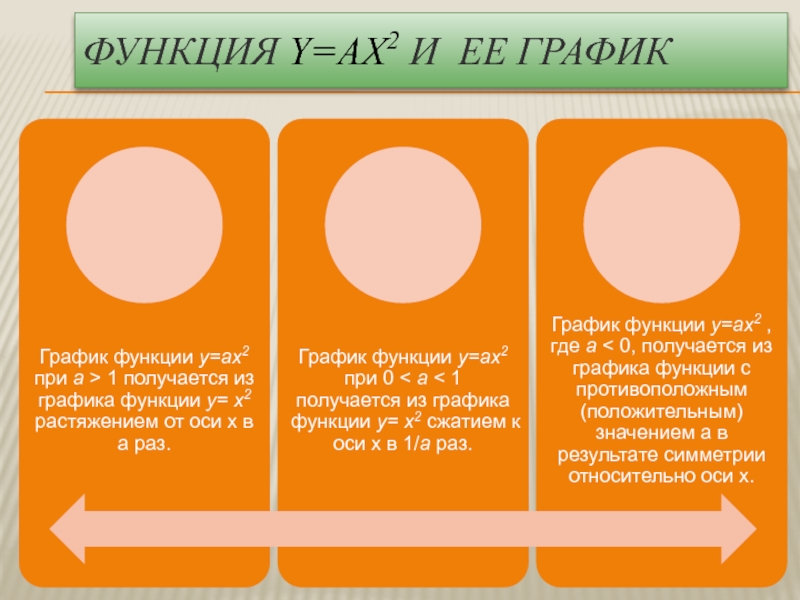
- 6. Функция y=ax2 и ее график
- 7. Слайд 7
- 8. Свойства функции y = ax2, при A > 0
- 9. Слайд 9
- 10. Свойства функции y = ax2, при A < 0
- 11. ДиктантВариант 1.1. Найдите все значения аргумента х,
- 12. ДиктантВариант 1.2. В каких четвертях расположен график
- 13. ДиктантВариант 1.3. Проходит ли график функции y
- 14. ДиктантВариант 1.4. Укажите промежуток возрастания функции y
- 15. ДиктантВариант 1.5. Графику функции y = ax2
- 16. ДиктантВариант 1.6. Сколько общих точек прямая y
- 17. Проверка
- 18. Y = ax2 + c, b =
- 19. Y = x2 и y = x2
- 20. Функция y=ax2 + bx + c
- 21. Слайд 21
- 22. Свойства функции y=ax2 + bx + c
- 23. Слайд 23
- 24. Слайд 24
Определение квадратичной функции Функцию, которую можно задать формулой вида y=ax2 + bx + c ,где х – независимая переменная, a, b и c – некоторые числа, причём a ≠ 0, называют квадратичной функцией.
Слайд 2Определение квадратичной функции
Функцию, которую можно задать формулой вида y=ax2 + bx
+ c ,где х – независимая переменная, a, b и c – некоторые числа, причём a ≠ 0, называют квадратичной функцией.
Слайд 11Диктант
Вариант 1.
1. Найдите все значения аргумента х, при каждом из которых
значение функции y = 1/3 x2 равно 3.
Вариант 2.
1. Найдите все значения аргумента х, при каждом из которых значение функции y = -1/4 x2 равно -4.
Вариант 2.
1. Найдите все значения аргумента х, при каждом из которых значение функции y = -1/4 x2 равно -4.
Слайд 12Диктант
Вариант 1.
2. В каких четвертях расположен график функции y = ax2
при a > 0.
Вариант 2.
2. В каких четвертях расположен график функции y = ax2 при a < 0.
Вариант 2.
2. В каких четвертях расположен график функции y = ax2 при a < 0.
Слайд 13Диктант
Вариант 1.
3. Проходит ли график функции y = -2x2 через точку
(-2; -8).
Вариант 2.
3. Проходит ли график функции y = -2x2 через точку (2; -8).
Вариант 2.
3. Проходит ли график функции y = -2x2 через точку (2; -8).
Слайд 14Диктант
Вариант 1.
4. Укажите промежуток возрастания функции y = -2x2.
Вариант 2.
4. Укажите
промежуток убывания функции y = -2x2.
Слайд 15Диктант
Вариант 1.
5. Графику функции y = ax2 принадлежит точка с координатами
(-2; 3), задайте формулой функцию.
Вариант 2.
5. Графику функции y = ax2 принадлежит точка с координатами (2; -3), задайте формулой функцию.
Вариант 2.
5. Графику функции y = ax2 принадлежит точка с координатами (2; -3), задайте формулой функцию.
Слайд 16Диктант
Вариант 1.
6. Сколько общих точек прямая y = x имеет с
параболой y = 4x2.
Вариант 2.
6. Сколько общих точек прямая y = -x имеет с параболой y = 4x2.
Вариант 2.
6. Сколько общих точек прямая y = -x имеет с параболой y = 4x2.
Слайд 18Y = ax2 + c, b = 0, a ≠ 0,
c ≠ 0.
y = x2 + 3
Какова область определения функции ?
Какова область значений функции ?
Показать что функция чётная, какая прямая является осью симметрии графика?
Нули функции.
Промежутки знакопостоянства.
Выяснить промежутки возрастания и убывания функции.
Чему равно наименьшее значение функции.
Слайд 19Y = x2 и y = x2 + 3
Для
любого значения x значения второй функции на 3 единицы больше соответствующего значения первой. График второй функции есть так же парабола, полученная переносом графика первой функции вверх параллельно оси ординат на 3 единицы
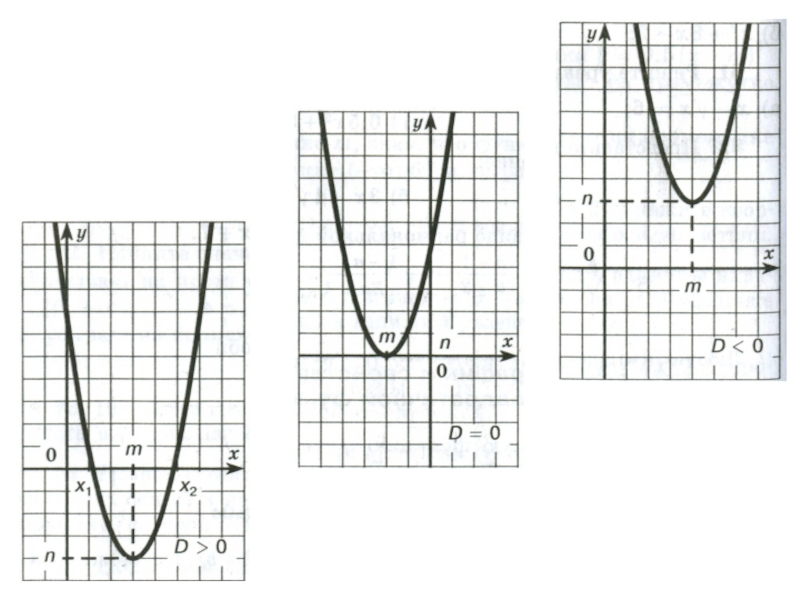
Слайд 22Свойства функции y=ax2 + bx + c при а > 0
Область
определения функции – множество действительных чисел
Область значений функции – множество [-D/4a ; + ∞)
Нули функции: y = 0
x1 = (-b-√D)/2a и x2 = (-b+√D)/2a при D > 0
x = -b/2a при D = 0
Функция нулей не имеет при D < 0
Промежутки знакопостоянства: y > 0, y < 0
Если D > 0, то y > 0 при xє(-∞ ; x1) и xє(x2; + ∞) и
y < 0 при xє(x1 ; x2)
Если D = 0, то y > 0 при любых xєR, кроме x = -b/2a.
Если D < 0, то y > 0 при любых xєR
Промежутки монотонности:
Функция убывает на промежутке (-∞ ; -b/2a]
Функция возрастает на промежутке [-b/2a ; +∞)
Наименьшее значение функции равно –D/4a при x = -b/2a
Область значений функции – множество [-D/4a ; + ∞)
Нули функции: y = 0
x1 = (-b-√D)/2a и x2 = (-b+√D)/2a при D > 0
x = -b/2a при D = 0
Функция нулей не имеет при D < 0
Промежутки знакопостоянства: y > 0, y < 0
Если D > 0, то y > 0 при xє(-∞ ; x1) и xє(x2; + ∞) и
y < 0 при xє(x1 ; x2)
Если D = 0, то y > 0 при любых xєR, кроме x = -b/2a.
Если D < 0, то y > 0 при любых xєR
Промежутки монотонности:
Функция убывает на промежутке (-∞ ; -b/2a]
Функция возрастает на промежутке [-b/2a ; +∞)
Наименьшее значение функции равно –D/4a при x = -b/2a