Презентация, доклад к уроку Классическое определение вероятности

Содержание

Исправьте ошибки

Слайд 1Блиц - опрос
1. Как называются различные комбинации выстраивания нескольких предметов друг

за другом?

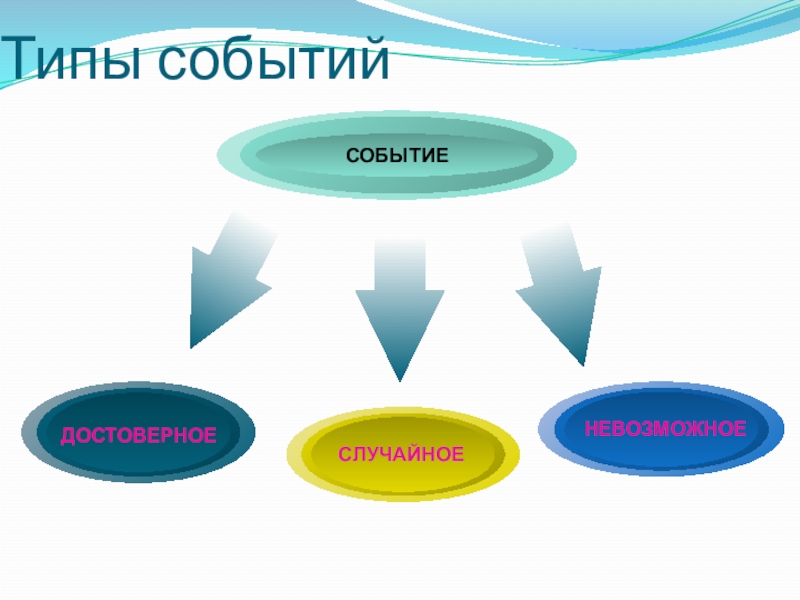
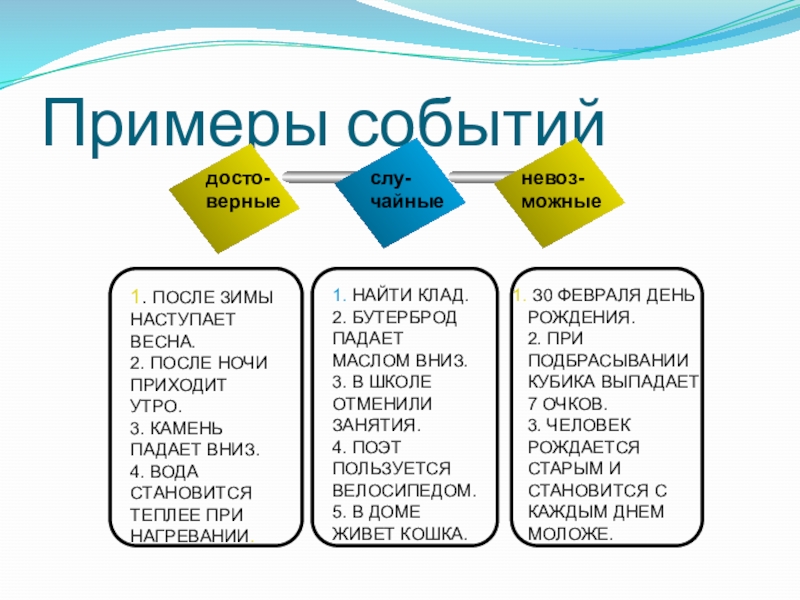
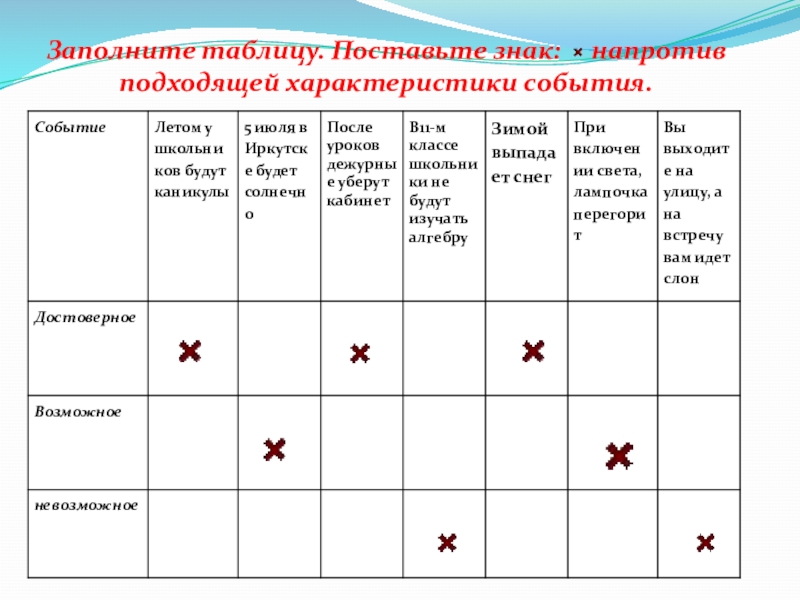
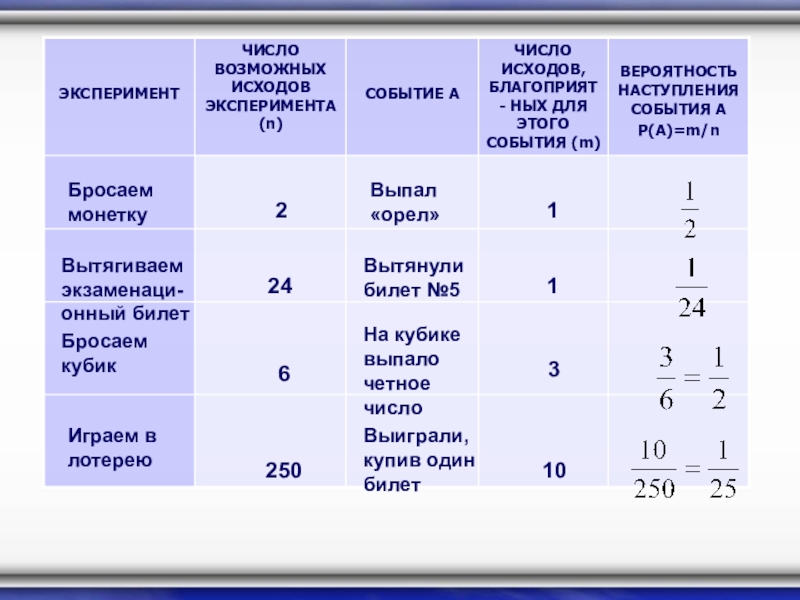
2. Что называют перестановками из n элементов?

3. Чем отличаются друг от друга две различные перестановки?

4. Рассчитайте число всевозможных перестановок из 9 книг на полке.

5. Как можно выбрать три книг из девяти для трёх победителей?

6. Что называется сочетанием из n элементов по к элементов?

Перестановками

Перестановками из n элементов называются комбинации
из n элементов, отличающиеся друг от друга
только порядком следования элементов.

Порядком следования

362800

Размещением 9-ти книг по 3.

Сочетанием из n элементов называются комбинации
из n элементов, отличающиеся друг от друга
только составом.

Блиц - опрос1. Как называются различные комбинации выстраивания нескольких предметов друг за другом?2. Что называют перестановками из

Слайд 2Исправьте ошибки

Исправьте ошибки

Слайд 3Классическое определение вероятности

Классическое определение вероятности

Слайд 4ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ.

Слайд 5СОБЫТИЕ

Под СОБЫТИЕМ понимается явление, которое происходит в

результате осуществления какого-либо определенного эксперимента.

ПРИМЕР. Бросаем шестигранный игральный кубик.
Определим события:
А {выпало четное число очков};
В {выпало число очков, кратное 3};
С {выпало более 4 очкков}.

✔

СОБЫТИЕ Под СОБЫТИЕМ понимается явление, которое происходит в результате осуществления какого-либо определенного

Слайд 6Эксперимент (опыт)
ЭКСПЕРИМЕНТ (или опыт) заключается в наблюдении за объектами

или явлениями в строго определенных условиях и измерении значений заранее определенных признаков этих объектов (явлений).

✔

Эксперимент (опыт) ЭКСПЕРИМЕНТ (или опыт) заключается в наблюдении за объектами или явлениями в строго определенных условиях

Слайд 7СЛУЧАЙНОЕ СОБЫТИЕ
СЛУЧАЙНЫМ называют событие, которое может произойти или не

произойти в результате некоторого испытания (опыта). Обозначают заглавными буквами А, В, С, Д,… (латинского алфавита).

✔

СЛУЧАЙНОЕ СОБЫТИЕ СЛУЧАЙНЫМ называют событие, которое может произойти или не произойти в результате некоторого испытания (опыта).

Слайд 8Рассмотрим несколько наиболее «излюбленных» в теории вероятностей примеров случайных экспериментов.

Рассмотрим несколько наиболее «излюбленных» в теории вероятностей примеров случайных экспериментов.

Слайд 9Опыт 1:
Подбрасывание монеты.
Испытание – подбрасывание

монеты; события – монета упала «орлом» или «решкой».

✔

«решка» - лицевая сторона монеты (аверс)

«орел» - обратная сторона монеты (реверс)

Опыт 1: Подбрасывание монеты. Испытание – подбрасывание монеты; события – монета упала «орлом» или

Слайд 10Опыт 2:
Подбрасывание кубика.
Это следующий по

популярности после монеты случайный эксперимент.
Испытание – подбрасывание кубика; события – выпало 1, 2, 3, 4, 5 или 6 очков (и другие).

✔

Опыт 2: Подбрасывание кубика. Это следующий по популярности после монеты случайный эксперимент. Испытание –

Слайд 11Опыт 3:
Выбор перчаток. В коробке лежат 3 пары

одинаковых перчаток. Из нее, не глядя, вынимаются две перчатки.







«Завтра днем – ясная погода».
Здесь наступление дня – испытание, ясная погода – событие.

✔

✔

Опыт 4:

Опыт 3: Выбор перчаток. В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя,

Слайд 12
События А и В называют несовместными ,если они не могут произойти

одновременно

События называют равновозможными , каждое из них е не имеет преимуществ в появлении чаще других.
События А и В называют несовместными ,если они не могут произойти одновременноСобытия называют равновозможными , каждое из

Слайд 13Типы событий
ДОСТОВЕРНОЕ
НЕВОЗМОЖНОЕ
СЛУЧАЙНОЕ



Типы событийДОСТОВЕРНОЕНЕВОЗМОЖНОЕСЛУЧАЙНОЕ

Слайд 14Типы событий
Событие называется
невозможным,

если оно не
может произойти
в результате
данного испытания.

Случайным
называют
событие которое может
произойти или не произойти в
результате
некоторого
испытания.

Событие
называется
достоверным,
если оно обязательно произойдет в
результате
данного испытания.

ДОСТОВЕРНОЕ

СЛУЧАЙНОЕ

НЕВОЗМОЖНОЕ

Типы событий Событие называется невозможным, если оно не

Слайд 15Примеры событий
досто-
верные
слу-
чайные
невоз-
можные
1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.
2. ПОСЛЕ НОЧИ ПРИХОДИТ УТРО.
3. КАМЕНЬ

ПАДАЕТ ВНИЗ.
4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ НАГРЕВАНИИ.

1. НАЙТИ КЛАД.
2. БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ.
3. В ШКОЛЕ ОТМЕНИЛИ ЗАНЯТИЯ.
4. ПОЭТ ПОЛЬЗУЕТСЯ ВЕЛОСИПЕДОМ.
5. В ДОМЕ ЖИВЕТ КОШКА.

З0 ФЕВРАЛЯ ДЕНЬ РОЖДЕНИЯ.
2. ПРИ ПОДБРАСЫВАНИИ КУБИКА ВЫПАДАЕТ 7 ОЧКОВ.
3. ЧЕЛОВЕК РОЖДАЕТСЯ СТАРЫМ И СТАНОВИТСЯ С КАЖДЫМ ДНЕМ МОЛОЖЕ.

Примеры событийдосто-верныеслу-чайныеневоз-можные1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.2. ПОСЛЕ НОЧИ ПРИХОДИТ УТРО.3. КАМЕНЬ ПАДАЕТ ВНИЗ.4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ

Слайд 16Какие из следующих событий – случайные, достоверные, невозможные:
черепаха научиться говорит;
вода в

чайнике, стоящим на горячей плите закипит;
ваш день рождения – 19 октября
день рождение вашего друга – 30 февраля;
вы выиграете участвуя в лотереи;
вы не выигрываете, участвуя в беспроигрышной лотереи;
вы проиграете партию в шахматы;
на следующей недели испортиться погода;
вы нажали на звонок, а он не зазвонил;
после четверга будет пятница;
после пятницы будет воскресенье.

Вспомним

НЕВОЗМОЖНОЕ

СЛУЧАЙНОЕ

СЛУЧАЙНОЕ

НЕВОЗМОЖНОЕ

СЛУЧАЙНОЕ

НЕВОЗМОЖНОЕ

СЛУЧАЙНОЕ

СЛУЧАЙНОЕ

СЛУЧАЙНОЕ

ДОСТОВЕРНОЕ

НЕВОЗМОЖНОЕ











Какие из следующих событий – случайные, достоверные, невозможные:черепаха научиться говорит;вода в чайнике, стоящим на горячей плите закипит;ваш

Слайд 17Заполните таблицу. Поставьте знак: напротив подходящей характеристики события.

Заполните таблицу. Поставьте знак: напротив подходящей характеристики события.

Слайд 18Охарактеризуйте события, о которых идет речь в приведенных заданиях как достоверные,

невозможные или случайные.

Петя задумал натуральное число. Событие состоит в следующем:

а) задумано четное число;
б) задумано нечетное число;
в) задумано число, не являющееся ни четным, ни нечетным;
г) задумано число, являющееся четным или нечетным.

Задание 1

Охарактеризуйте события, о которых идет речь в приведенных заданиях как достоверные, невозможные или случайные.Петя задумал натуральное число.

Слайд 19Задание 2
В мешках лежит 10 шаров: 3 синих, 3 белых

и 4 красных.

Охарактеризуйте следующее событие:

а) из мешка вынули 4 шара и они все синие;
б) из мешка вынули 4 шара и они все красные;
в) из мешка вынули 4 шара, и все они оказались разного цвета;
г) из мешка вынули 4 шара, и среди них не оказалось шара черного цвета.
Задание 2 В мешках лежит 10 шаров: 3 синих, 3 белых и 4 красных. Охарактеризуйте следующее событие:а)

Слайд 20ИСХОД
ИСХОДОМ (или элементарным исходом, элементарным событием) называется один

из взаимоисключающих друг друга вариантов, которым может завершиться случайный эксперимент.

✔

ИСХОД ИСХОДОМ (или элементарным исходом, элементарным событием) называется один из взаимоисключающих друг друга вариантов, которым

Слайд 21Число возможных исходов в каждом из рассмотренных выше опытах.
Опыт

1. – 2 исхода: «орел», «решка».

Опыт 2. – 6 исходов: 1, 2, 3, 4, 5, 6.

Опыт 3. – 3 исхода: «обе перчатки на левую руку», «обе перчатки на правую руку», «перчатки на разные руки».

✔

✔

✔

Число возможных исходов в каждом из рассмотренных выше опытах. Опыт 1. – 2 исхода: «орел», «решка».

Слайд 22Благоприятный исход:
Исход испытания называется благоприятным событию А ,если его наступление в

результате опыта приводит к наступлению события А
Благоприятный исход: Исход испытания называется благоприятным событию А ,если его наступление в результате опыта приводит к наступлению

Слайд 23Зажмурьте глаза и укажите ручкой точку на карте.
Вопрос: Какова вероятность

того, что эта точка окажется на территории России?
Зажмурьте глаза и укажите ручкой точку на карте. Вопрос: Какова вероятность того, что эта точка окажется на

Слайд 24Для ответа на этот вопрос нужно знать, какую часть всей карты

занимает Россия. Точнее, какую часть всей площади карты составляет Россия.

 

 

Решение:

Для ответа на этот вопрос нужно знать, какую часть всей карты занимает Россия. Точнее, какую часть всей

Слайд 25Классическое определение вероятности

Классическое определение вероятности

Слайд 26«…Все в природе подлежит измерению, все может быть сосчитано».
Н. И. Лобачевский


Классическая вероятность события

Р(А)=

«…Все в природе подлежит измерению, все может быть сосчитано».Н. И. Лобачевский Классическая вероятность событияР(А)=

Слайд 27Основные задачи

Основные задачи

Слайд 28Какова вероятность того, что из 5 цыплят один будет синего цвета?

Какова вероятность того, что из 5 цыплят один будет синего цвета?

Слайд 29Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24

1
Бросаем кубик

На кубике выпало

четное число


6


3

Играем в лотерею

Выиграли, купив один билет


250


10

Бросаем монетку2Выпал «орел»1Вытягиваем экзаменаци- онный билетВытянули билет №5241Бросаем кубикНа кубике выпало четное число63Играем в лотереюВыиграли, купив один

Слайд 30На экзамене -24 билета. Андрей не разобрался в одном билете и

очень боится его вытянуть. Какова вероятность, что Андрею достанется несчастный билет?
А- достанется несчастливый билет
n - _______;
m =__________, Тогда Р(А)=

Задачи

В лотереи 10 выигрышных билетов и 240 билетов без выигрыша. Какова вероятность выиграть в эту лотерею, купив один билет?
А- выиграть
Исходов всего 240+10=250;
Шансы=10; Р(А)=

В лотереи 100 билетов, из них 5 выигрышных. Какова вероятность проигрыша
А- проиграть:
Исходов _______;
Шанс =100-5=95, тогда Р(А)=

На экзамене -24 билета. Андрей не разобрался в одном билете и очень боится его вытянуть. Какова вероятность,

Слайд 31Пример 1
В школе 1300 человек, из

них 5 человек хулиганы.
Какова вероятность того, что один из них попадётся директору на глаза?
Пример 1 В школе 1300 человек, из них

Слайд 32Вероятность:
P(A) = 5/1300 = 1/250.
Решение

Вероятность: P(A) = 5/1300 = 1/250.Решение

Слайд 33Ошибка Даламбера

Какова вероятность, что подброшенные вверх две правильные монеты упадут

на одну и ту же сторону?
Решение, предложенное Даламбером.
Опыт имеет три равновозможных исхода:
Обе монеты упали на «орла».
Обе монеты упали на «решку».
Одна из монет упала на «орла», другая на «решку».

N = 3; N(A) = 2; P(A) =

Ошибка Даламбера Какова вероятность, что подброшенные вверх две правильные монеты упадут на одну и ту же сторону?

Слайд 34Правильное решение.
Орел, орел
Решка, решка
Орел, решка
Решка, орел
n = ; m

= ;

P(A) =

Нельзя объединять два принципиально разных исхода в один. Природа различает все предметы.

4

2

Правильное решение. Орел, орелРешка, решкаОрел, решкаРешка, орелn = ; m = ; P(A) = Нельзя объединять

Слайд 35Задача
В квадрат со стороной 10 см «бросают» точку. Какова вероятность того,

что эта точка попадёт в круг, вписанный в квадрат? Радиус круга равен 2 см.

РЕШЕНИЕ:


 

 

 

ЗадачаВ квадрат со стороной 10 см «бросают» точку. Какова вероятность того, что эта точка попадёт в круг,

Слайд 36Пример 2.
При игре в нарды бросают 2 игральных кубика. Какова

вероятность того, что на обоих кубиках выпадут одинаковые числа?
Пример 2. При игре в нарды бросают 2 игральных кубика. Какова вероятность того, что на обоих кубиках

Слайд 37Решение
Составим следующую таблицу
Вероятность: P(A)=6/36= =1/6.

РешениеСоставим следующую таблицуВероятность: P(A)=6/36= =1/6.

Слайд 38









Пример 3.
Из карточек составили слово «статистика». Какую карточку с буквой вероятнее

всего вытащить? Какие события равновероятные?

с

т

а

т

и

с

т

и

к

а

Пример 3.Из карточек составили слово «статистика». Какую карточку с буквой вероятнее всего вытащить? Какие события равновероятные?статистика

Слайд 39Всего 10 букв.
Буква «с» встречается 2 раза –
P(с) = 2/10

= 1/5;
буква «т» встречается 3 раза –
P(т) = 3/10;
буква «а» встречается 2 раза –
P(а) = 2/10 = 1/5;
буква «и» встречается 2 раза –
P(и) = 2/10 = 1/5;
буква «к» встречается 1 раз –
P(к) = 1/10.

Решение

Всего 10 букв.Буква «с» встречается 2 раза – P(с) = 2/10 = 1/5;буква «т» встречается 3 раза

Слайд 40

Задача 1.
В коробке 4 синих, 3 белых и 2 желтых

фишки. Они тщательно перемешиваются, и наудачу извлекается одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой. 
Задача 1. В коробке 4 синих, 3 белых и 2 желтых фишки. Они тщательно перемешиваются, и наудачу

Слайд 41

а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность равна:
P=3:9=1/3=0,33(3)
б)

Мы имеем всевозможных случаев 9. Благоприятствующих событий 2. Вероятность равна P=2:9=0,2(2)
в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=0,7(7)

Решение

а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность равна:P=3:9=1/3=0,33(3)б) Мы имеем всевозможных случаев 9. Благоприятствующих

Слайд 42

Задача 2.
В коробке лежат 10 одинаковых шаров, на каждом из

которых написан его номер от 1 до 10. Найдите вероятность следующих событий: а) извлекли шар № 7; б) номер извлеченного шара – четное число; в) номер извлеченного шара кратен 3. 
Задача 2. В коробке лежат 10 одинаковых шаров, на каждом из которых написан его номер от 1

Слайд 43

Задача 3.
Мальчики играли в “Орлянку”. Но монетка куда-то закатилась. Предложите,

как заменить ее игральным кубиком?
Задача 3. Мальчики играли в “Орлянку”. Но монетка куда-то закатилась. Предложите, как заменить ее игральным кубиком?

Слайд 44

Считать "орел" -  четное число, а "решка" - не четное число. 
Решение

Считать

Слайд 45

Задача 5.
В настольной игре сломалась вертушка с тремя разными секторами:

красным, белым и синим, но есть кубик. Как заменить вертушку? 
Задача 5. В настольной игре сломалась вертушка с тремя разными секторами: красным, белым и синим, но есть

Слайд 46

Считать на кубике 1 и 2 - красный сектор, 3 и

4 - синий сектор, 5 и 6 - белый сектор.

Решение

Считать на кубике 1 и 2 - красный сектор, 3 и 4 - синий сектор, 5 и

Слайд 47Самостоятельная работа
1 вариант
2 вариант
1. В урне 10 шаров: 6 белых и

4 черных. Вынули один шар. Какова вероятность, что он чёрный?

1. В урне 15 шаров: 5 синих и 10 черных. Вынули один шар. Какова вероятность, что он синий?

2. Из колоды карт вынимают одну карту? Какова вероятность появления карты червовой масти?

2. Из колоды карт вынимают одну карту? Какова вероятность появления короля?

3. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

3. На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.

Самостоятельная работа1 вариант2 вариант1. В урне 10 шаров: 6 белых и 4 черных. Вынули один шар. Какова

Слайд 48Подведение итогов:
Что такое событие?
Какое событие называют действительным?
Какое событие называют случайным?
Какое

событие называют достоверным, невозможным?
Что такое исход испытания?
Подведение итогов: Что такое событие?Какое событие называют действительным?Какое событие называют случайным?Какое событие называют достоверным, невозможным? Что такое

Слайд 49Классическая формула вероятности
Вероятность события- это численная мера объективной возможности ее появления.

Если имеется полная группа попарно несовместных и равновозможных событий, то вероятность Р(А) наступления события А вычисляется как отношение числа исходов, благоприятствующих наступлению события, к числу всех исходов испытания.

N – число всех исходов испытания
М – число исходов благоприятствующих событию А

Свойство вероятности:
1) Вероятность достоверного события равна 1

2) Вероятность невозможного события равна 0

3) Вероятность события А удовлетворяет двойному неравенству

Классическая формула вероятностиВероятность события- это численная мера объективной возможности ее появления. Если имеется полная группа попарно несовместных

Слайд 50Домашнее задание:
1.Составить 2 задачи на вероятность.
2.Написать реферат на одну из тем:


Даниил Бернулли и его вклад в развитие теории вероятностей.
Гюйгенс и его вклад в развитие теории вероятностей
Блез Паскаль и его вклад в развитие теории вероятностей
Ферма и его вклад в развитие теории вероятностей

Домашнее задание:1.Составить 2 задачи на вероятность.2.Написать реферат на одну из тем: Даниил Бернулли и его вклад в

Слайд 52
В магазин поступило 30 холодильников, пять из которых имеют заводской дефект.

Случайным образом выбирают один холодильник. Какова вероятность того, что он будет без дефекта?
Набирая номер телефона, абонент забыл две последние цифры, но помнит, что одна из них – ноль, а другая – нечётная. Найти вероятность того, что он наберёт правильный номер.
Найти вероятность того, что при бросании двух игральных костей в сумме выпадет:
а) пять очков; б) не более четырёх очков; в) от 3 до 9 очков включительно.

В магазин поступило 30 холодильников, пять из которых имеют заводской дефект. Случайным образом выбирают один холодильник. Какова

Слайд 53Литература
Ю.Н.Макарычев, Н.Г.Миндюк. Начальные сведения из теории вероятностей в школьном курсе

алгебры. “Математика в школе”. № 7. 2004 г. стр. 24.
В.А.Булычев, Е.А.Бунимович. Изучение теории вероятностей и статистики в школьном курсе математики. “Математика в школе”. № 4. 2003 г. стр. 59.
Электронные источники информации
Бунимович Е.А., Булычев В.А. Вероятность и статистика 5-9. Электронное учебное пособие на CD-ROM. – М.: Дрофа, 2003.
www.teorver.ru
http://ru.wikipedia.org/wiki/Теория_вероятности

Литература Ю.Н.Макарычев, Н.Г.Миндюк. Начальные сведения из теории вероятностей в школьном курсе алгебры. “Математика в школе”. № 7.
Скачать презентацию

Похожие презентации

Презентация по алгебре Решение показательных уравнений Презентация по алгебре Решение показательных уравнений 204
Презентация внеурочного занятия по математике для учащихся 7-9 классов Презентация внеурочного занятия по математике для учащихся 7-9 классов 250
Презентация к уроку алгебры в 8 классе Степень с целым отрицательным показателем. Презентация к уроку алгебры в 8 классе Степень с целым отрицательным показателем. 447
Презентация по теме: Решение задач на концентрацию, сплавы, движение (9-11 классы) Презентация по теме: Решение задач на концентрацию, сплавы, движение (9-11 классы) 265
Презентация по математике для 8-9 класса Решение неполных квадратных уравнений Презентация по математике для 8-9 класса Решение неполных квадратных уравнений 273
Презентация по математике Линейная функция, её свойства и график 7 класс Презентация по математике Линейная функция, её свойства и график 7 класс 217

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть