- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Исследование связи между корнями и коэффициентами квадратного уравнения.
Содержание
- 1. Презентация к уроку Исследование связи между корнями и коэффициентами квадратного уравнения.
- 2. Тема: «Исследование связи
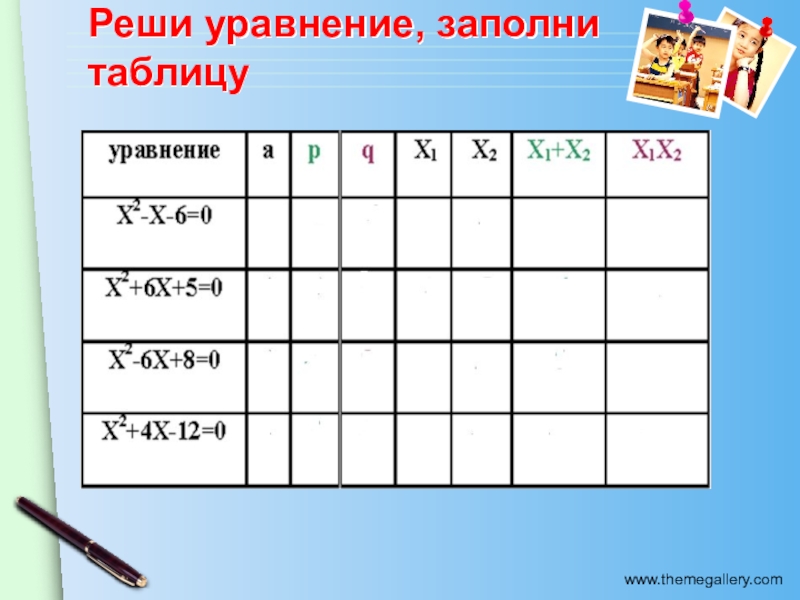
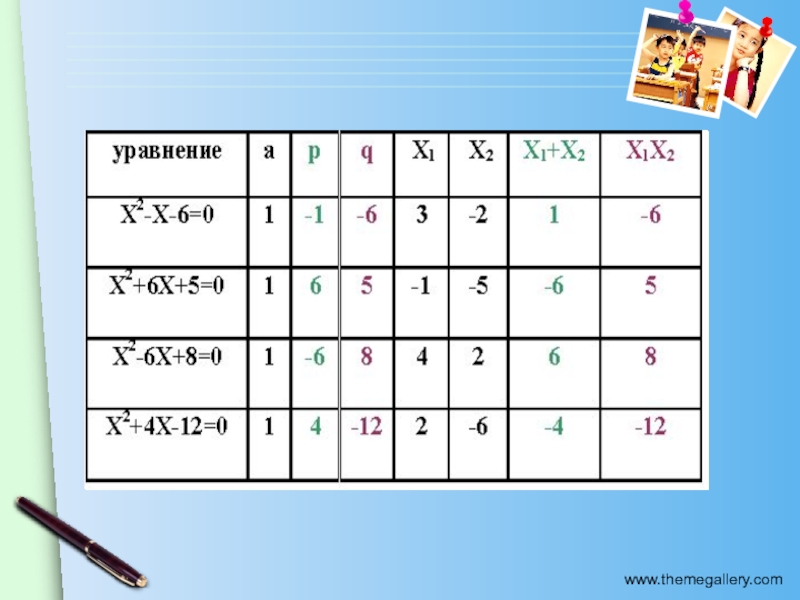
- 3. Реши уравнение, заполни таблицу
- 4. Слайд 4
- 5. Утверждение №1: Пусть х1 и х2 –
- 6. Теорема Виета: Числа х1 и х2 являются
- 7. Велик гармонией своей Квадратный многочлен: Произведение корней
- 8. Франсуа Виет Родился в 1540 году во
- 9. Слайд 9
- 10. Ситуации, в которых может использоваться теорема Виета.
- 11. Решите следующие задания: 1.Верно ли, что
- 12. Обобщенная теорема Виета: Числа х1 и
- 13. Решите следующие задания: 1.В уравнении х2 +
- 14. По праву достойна в стихах быть воспета
Тема: «Исследование связи между корнями и коэффициентами
Слайд 5Утверждение №1: Пусть х1 и х2 – корни уравнения
х2+ pх + q = 0.
Тогда числа х1, х2 , p, q связаны равенствами:
х1 + х2= -p, х1х2=q
Утверждение № 2:
Пусть числа х1, х2, p,q связаны равенствами х1 + х2 = -p, х1х2=q.
Тогда х1 и х2 – корни уравнения
х2+ pх + q=0
Слайд 6Теорема Виета: Числа х1 и х2 являются корнями приведенного квадратного уравнения х2
+ pх + q = 0 тогда и только тогда, когда х1 +х2 = -p, х1х2 = q.
Следствие:
х2 + pх + q=(х-х1)(х-х2).
Слайд 7Велик гармонией своей Квадратный многочлен: Произведение корней — Его свободный член. Другой чарующий момент — Что
минус сумма их
Суть средний коэффициент.
Запомни этот стих!
Павел Кикоть
Слайд 8Франсуа Виет
Родился в 1540 году во Франции.
Отец Виета был прокурором. Сын выбрал профессию отца и стал юристом, окончив университет в Пуату.
В 1563 году он оставляет юриспруденцию и становится учителем в знатной семье. Преподавание побудило в молодом юристе интерес к математике. Виет переезжает в Париж, где легче узнать о достижениях ведущих математиков Европы.
С 1571 года Виет занимает важные государственные посты, но в 1584 году он был отстранен и выслан из Парижа. Теперь он имел возможность всерьез заняться математикой.
В 1563 году он оставляет юриспруденцию и становится учителем в знатной семье. Преподавание побудило в молодом юристе интерес к математике. Виет переезжает в Париж, где легче узнать о достижениях ведущих математиков Европы.
С 1571 года Виет занимает важные государственные посты, но в 1584 году он был отстранен и выслан из Парижа. Теперь он имел возможность всерьез заняться математикой.
Слайд 9
Франсуа Виет
В 1591 году он издает трактат «Введение в аналитическое искусство», где показал, что, оперируя с символами, можно получить результат, применимый к любым соответствующим величинам. Знаменитая теорема была обнародована в том же году.
Громкую славу получил при Генрихе lll во время Франко-Испанской войны. В течение двух недель, просидев за работой дни и ночи, он нашел ключ к Испанскому шифру.
Умер в Париже в 1603 году, есть подозрения, что он был убит.
В 1591 году он издает трактат «Введение в аналитическое искусство», где показал, что, оперируя с символами, можно получить результат, применимый к любым соответствующим величинам. Знаменитая теорема была обнародована в том же году.
Громкую славу получил при Генрихе lll во время Франко-Испанской войны. В течение двух недель, просидев за работой дни и ночи, он нашел ключ к Испанскому шифру.
Умер в Париже в 1603 году, есть подозрения, что он был убит.
Слайд 10Ситуации, в которых может использоваться теорема Виета. 1.Проверка правильности найденных корней. ☻ 2.Определение знаков
корней квадратного уравнения.
☻
3.Устное нахождение целых корней приведенного квадратного уравнения.
☻
4.Составление квадратных уравнений с заданными корнями.
☻
5.Разложение квадратного трехчлена на множители.
Слайд 11Решите следующие задания: 1.Верно ли, что числа 15 и 7 являются
корнями уравнения х2 - 22х + 105 = 0?
☻
2.Определите знаки корней уравнения
х2 + 5х – 36 = 0.
☻
3. Найдите устно корни уравнения
х2 - 9х + 20 = 0.
☻
3.Составьте квадратное уравнение, корнями которого являются числа 1/3 и 0,3.
☻
4.Разложите квадратный трехчлен на множители х2 + 2х - 48.
Слайд 12Обобщенная теорема Виета: Числа х1 и х2 являются корнями квадратного уравнения
ах2 + bх + с = 0 тогда и только тогда, когда
х1 + х2 = -b/а, х1 х2 = с/а.
Следствие:
ах2 + bх + c = а(х-х1)(х-х2).
Слайд 13Решите следующие задания: 1.В уравнении х2 + pх – 32 = 0
один из корней равен 7. Найдите другой корень и коэффициент p.
2.Один из корней уравнения
10х2 - 33х + с = 0 равен 5,3. Найдите другой корень и коэффициент с.
3.Разность корней квадратного уравнения х2 - 12х + q = 0 равна 2. Найдите q.
4.Определите знаки корней квадратного уравнения ( если они существуют), не решая уравнения: 5х2 – х – 108 = 0.
5.Найдите b и решите уравнение
(b-1) х2 - (b+1)х = 72, если х1 = 3.
Слайд 14По праву достойна в стихах быть воспета О свойствах корней теорема Виета. Что
лучше, скажи, постоянства такого –
Умножить ты корни, и дробь уж готова:
В числителе «с», в знаменателе «а».
И сумма корней тоже дроби равна,
Хоть с минусом дробь та, ну, что за беда:
В числителе «в», в знаменателе «а».