- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры Системы уравнений 11 класс
Содержание
- 1. Презентация к уроку алгебры Системы уравнений 11 класс
- 2. Устная работаНайдите значение выражения:5:0,2-13=(5,7*10-3):)(1,9*10-2)(3-3)2 /3-104,5*102 /9*104(2√5)2 /10Log5150-log56Log183+log186120,3810,005221
- 3. Устная работаРешить уравнение8 5+х=64Х2+3х=0Х2=-14-9хLog2(2+x)=log211Х=-3Х1=0,х2=-3Х1=-7,х2=-2Х=9
- 4. Слайд 4
- 5. Посмотрите на картинку, скажите как она может быть связана с темой уроком?
- 6. Солнечная система Система уравнений
- 7. Системы уравнений
- 8. Если поставлена задача- найти такие пары чисел
- 9. Вопросы:1. Что называется решением системы уравнений?Пару значений
- 10. Методы решения
- 11. Задание (работа в группах)Определить метод решения системы уравненийСоставить алгоритм
- 12. Метод подстановки Выразить из какого-нибудь уравнения системы
- 13. Метод сложенияУмножьте почленно уравнения системы, подбирая множители
- 14. Графический метод Построить график функции, заданной
- 15. Метод введения новой переменной Ввести одну или две
- 16. методы решения:Метод подстановкиМетод сложенияГрафический методМетод введения новой переменной
- 17. ВНИМАНИЕ! При решении систем уравнений, мы практически
- 18. ВНИМАНИЕ! Равносильными являются методы: 1. Метод подстановки. 2. Метод сложения. 3.
- 19. Работа в группах(5 мин)Каждая группа решают по одной системе уравнений
- 20. Круговорот-Беспрерывный процесс, с постоянным возвращением к исходному
- 21. А) метод подстановки б) метод сложения в) метод введения новой переменной г) графический метод1.2.3.4.5.6.
- 22. а) метод подстановки- 1,3 б) метод сложения-2,5 в) метод введения новой переменной-4,6 г) графический метод-
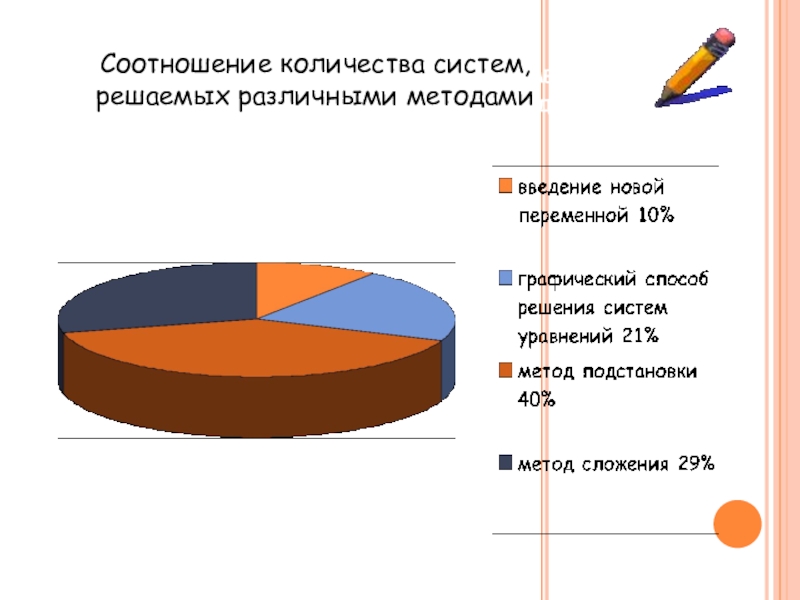
- 23. Соотношение количества систем, решаемых методом введения новых
- 24. ИТОГ УРОКА
- 25. Домашнее задание § 59Выбрать 4 системы и решить их различными методами
- 26. Слайд 26
Устная работаНайдите значение выражения:5:0,2-13=(5,7*10-3):)(1,9*10-2)(3-3)2 /3-104,5*102 /9*104(2√5)2 /10Log5150-log56Log183+log186120,3810,005221
Слайд 2Устная работа
Найдите значение выражения:
5:0,2-13=
(5,7*10-3):)(1,9*10-2)
(3-3)2 /3-10
4,5*102 /9*104
(2√5)2 /10
Log5150-log56
Log183+log186
12
0,3
81
0,005
2
2
1
Слайд 3Устная работа
Решить уравнение
8 5+х=64
Х2+3х=0
Х2=-14-9х
Log2(2+x)=log211
Х=-3
Х1=0,х2=-3
Х1=-7,х2=-2
Х=9
Слайд 8
Если поставлена задача- найти такие пары чисел (х;у), которые одновременно удовлетворяют
уравнению p(x;y)=0 и уравнению q(x;y)=0, то говорят, что данные уравнения образуют …
систему уравнений
p(x;y)=0
q(x;y)=0
систему уравнений
p(x;y)=0
q(x;y)=0
Слайд 9Вопросы:
1. Что называется решением системы уравнений?
Пару значений (х;у), которая одновременно является
решением первого и второго уравнений системы , называют решением системы уравнений.
Что значит решить систему уравнений?
Решить систему уравнений- значит найти все ее решения или установить, что решений нет
Что значит решить систему уравнений?
Решить систему уравнений- значит найти все ее решения или установить, что решений нет
Слайд 12Метод подстановки
Выразить из какого-нибудь уравнения системы одну переменную через другую.
Подставить в
другое уравнение системы вместо этой переменной полученное выражение.
Решить получившееся уравнение с одной переменной.
Найти соответствующее значение второй переменной.
Записать ответ в виде пары чисел (х;у)
Решить получившееся уравнение с одной переменной.
Найти соответствующее значение второй переменной.
Записать ответ в виде пары чисел (х;у)
Слайд 13Метод сложения
Умножьте почленно уравнения системы, подбирая множители так, чтобы коэффициенты при
одной из переменных стали противоположными числами.
Сложите почленно левые и правые части уравнений системы.
Решите получившееся уравнение с одной переменной.
Найдите соответствующее значение второй переменной
Записать ответ в виде пары чисел (х;у)
Сложите почленно левые и правые части уравнений системы.
Решите получившееся уравнение с одной переменной.
Найдите соответствующее значение второй переменной
Записать ответ в виде пары чисел (х;у)
Слайд 14Графический метод
Построить график функции, заданной первым уравнением системы.
Построить график функции,
заданной вторым уравнением системы.
Определить координаты точек пересечения графиков функций
Записать ответ в виде пары чисел (х;у)
Определить координаты точек пересечения графиков функций
Записать ответ в виде пары чисел (х;у)
Слайд 15Метод введения новой переменной
Ввести одну или две новые переменные.
Записать новое уравнение
или систему уравнений.
Решить новое уравнение или систему уравнений и найти значения введённых переменных.
Сделать обратную замену и найти значения переменных из условия.
Записать ответ.
Решить новое уравнение или систему уравнений и найти значения введённых переменных.
Сделать обратную замену и найти значения переменных из условия.
Записать ответ.
Слайд 16методы решения:
Метод подстановки
Метод сложения
Графический метод
Метод введения новой переменной
Слайд 17ВНИМАНИЕ!
При решении систем уравнений, мы практически в полной мере руководствуемся
теми же принципами, что и при решении обычных уравнений.
Постепенно переходим к более простым уравнениям, выполняя равносильные преобразования.
К уравнениям следствиям мы так же можем переходить, но стоит не забывать, что в этом случае мы должны проверить все полученные корни.
Определение. Две системы уравнений называются равносильными, если они имеют одни и те же решения или если решений нет у каждой из систем.
Постепенно переходим к более простым уравнениям, выполняя равносильные преобразования.
К уравнениям следствиям мы так же можем переходить, но стоит не забывать, что в этом случае мы должны проверить все полученные корни.
Определение. Две системы уравнений называются равносильными, если они имеют одни и те же решения или если решений нет у каждой из систем.
Слайд 18ВНИМАНИЕ!
Равносильными являются методы:
1. Метод подстановки.
2. Метод сложения.
3. Метод введения новой переменой.
Используя
эти методы, мы заменяем исходную систему уравнений равносильной системой, но как правило получившуюся систему решить гораздо проще.
Методы, приводящие к уравнениям следствиям:
1. Возведение в квадрат обеих частей уравнения.
2. Умножение уравнений системы.
3. Преобразования, расширяющие область допустимых значений каждого уравнения.
При использовании данных методов, проверку корней следует проводить всегда!
Методы, приводящие к уравнениям следствиям:
1. Возведение в квадрат обеих частей уравнения.
2. Умножение уравнений системы.
3. Преобразования, расширяющие область допустимых значений каждого уравнения.
При использовании данных методов, проверку корней следует проводить всегда!
Слайд 20Круговорот
-Беспрерывный процесс, с постоянным возвращением к исходному положению, к началу.
Группа решает
данное задание, затем один человек из группы идет консультировать другую группу о своем методе решения системы уравнений.
Слайд 21А) метод подстановки
б) метод сложения
в) метод введения новой переменной
г) графический метод
1.
2.
3.
4.
5.
6.
Слайд 22
а) метод подстановки- 1,3
б) метод сложения-2,5
в) метод введения новой переменной-4,6
г)
графический метод-
Слайд 23Соотношение количества систем, решаемых методом введения новых переменных, с другими методами.
Соотношение
количества систем, решаемых различными методами