- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры по теме Квадратное неравенство и его решения (9 класс)
Содержание
- 1. Презентация к уроку алгебры по теме Квадратное неравенство и его решения (9 класс)
- 2. Найдите у=0, у>0, у
- 3. Слайд 3
- 4. ах2+вх+с>0 (ах2+вх+с
- 5. 1) х2+2х-4805) 7х+2х2>4 6) 5х2-у>07) х-3
- 6. 1. Направление ветвей параболы;2. Примерное расположение параболы;3. Координаты вершины параболы;4. Пересечение параболы с осями координат;5. Знак дискриминанта квадратного трехчлена.Выбрать из перечисленных:
- 7. Слайд 7
- 8. Задания группам: Разложить в хронологическом порядке шаги
- 9. Алгоритм решения квадратного неравенства 1.Привести неравенство к
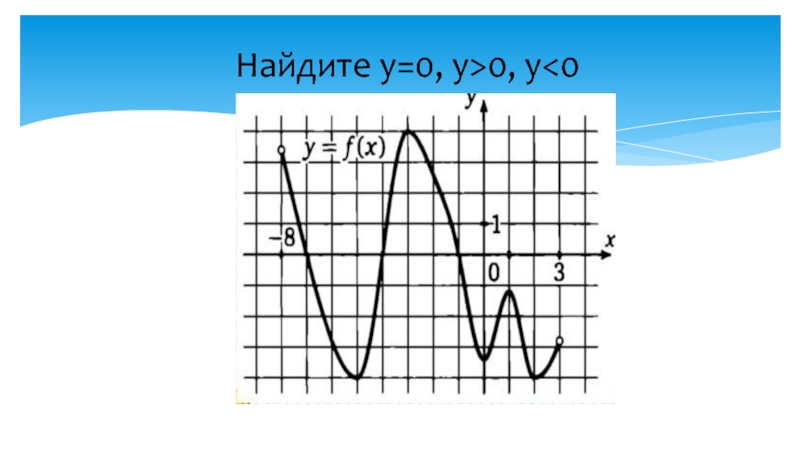
Найдите у=0, у>0, у
Слайд 1Проверка домашнего задания
№1 4
№2 4
№3 4
№4 1
№5 2
Критерии оценки:
5 «+» отметка 5 4 «+» отметка 4
3 «+» отметка 3 1-2 «+» отметка 2
Слайд 4 ах2+вх+с>0 (ах2+вх+с
некоторые числа, причем а≠0 называется неравенством второй степени или квадратным неравенством
Слайд 51) х2+2х-48
4) 3х-17х2>0
5) 7х+2х2>4
6) 5х2-у>0
7) х-3<0
8) -3х2-6х+9<0
9) -20х2≥5
Выбрать номера квадратных неравенств с одной переменной
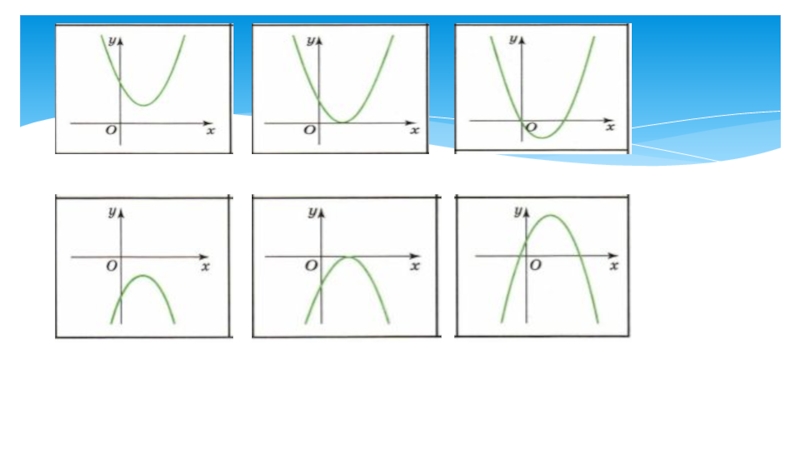
Слайд 61. Направление ветвей параболы;
2. Примерное расположение параболы;
3. Координаты вершины параболы;
4. Пересечение параболы с осями координат;
5. Знак
дискриминанта квадратного трехчлена.
Выбрать из перечисленных:
Слайд 8Задания группам: Разложить в хронологическом порядке шаги алгоритма решения квадратного неравенства
Схематически
построить график функции y = aх2 + bx + c.
Привести неравенство к виду aх2 + bx + c> 0 (aх2 + bx + c< 0).
Записать ответ в виде промежутка.
Найти точки пересечения параболы с осью абсцисс, решив для этого квадратное уравнение aх2 + bx + c =0.
На оси абсцисс выделить те значения x, для которых y> 0 (y< 0).
Выделить ту часть параболы, для которой y> 0 (y< 0).
Указать направление ветвей параболы ( если a>0, то ветви направлены вверх; если a<0, то ветви направлены вниз).
Рассмотреть функцию y = aх2 + bx + c.
Привести неравенство к виду aх2 + bx + c> 0 (aх2 + bx + c< 0).
Записать ответ в виде промежутка.
Найти точки пересечения параболы с осью абсцисс, решив для этого квадратное уравнение aх2 + bx + c =0.
На оси абсцисс выделить те значения x, для которых y> 0 (y< 0).
Выделить ту часть параболы, для которой y> 0 (y< 0).
Указать направление ветвей параболы ( если a>0, то ветви направлены вверх; если a<0, то ветви направлены вниз).
Рассмотреть функцию y = aх2 + bx + c.
Слайд 9Алгоритм решения квадратного неравенства
1.Привести неравенство к виду ах2+ bx +
c> 0 (ax2+ bx + c< 0).
2. Рассмотреть функцию y = ах2+ bx + c.
3. Указать направление ветвей параболы ( еслиa>0, то ветви направлены вверх; если a<0, то ветви направлены вниз).
4. Найти точки пересечения параболы с осью абсцисс, решив для этого квадратное уравнение ах 2+ bx + c =0.
5. Схематически построить график функции y = ax2+ bx + c.
6. Выделить ту часть параболы, для которой y> 0 (y< 0).
7. На оси абсцисс выделить те значения x, для которых y> 0 (y< 0).
8. Записать ответ в виде промежутка.
2. Рассмотреть функцию y = ах2+ bx + c.
3. Указать направление ветвей параболы ( еслиa>0, то ветви направлены вверх; если a<0, то ветви направлены вниз).
4. Найти точки пересечения параболы с осью абсцисс, решив для этого квадратное уравнение ах 2+ bx + c =0.
5. Схематически построить график функции y = ax2+ bx + c.
6. Выделить ту часть параболы, для которой y> 0 (y< 0).
7. На оси абсцисс выделить те значения x, для которых y> 0 (y< 0).
8. Записать ответ в виде промежутка.