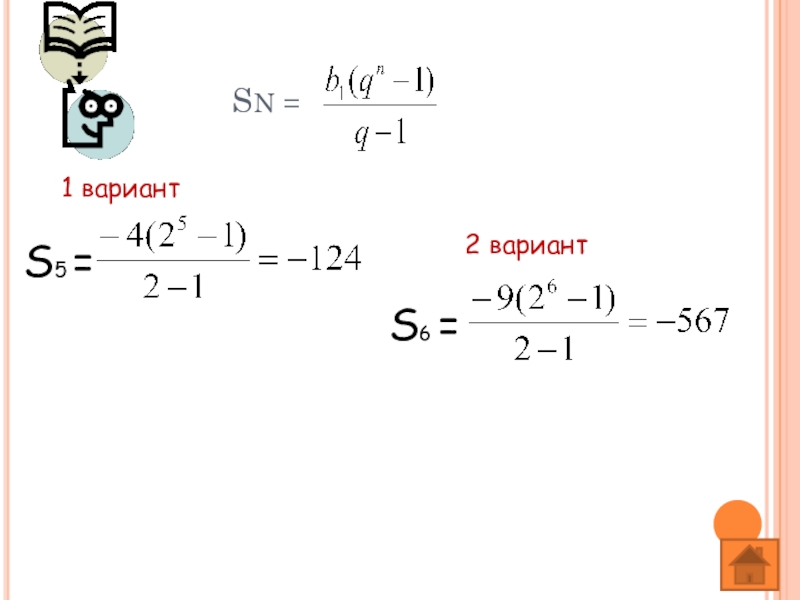- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры на тему Формула суммы n первых членов геометрической прогрессии
Содержание
- 1. Презентация к уроку алгебры на тему Формула суммы n первых членов геометрической прогрессии
- 2. Математические знания могут применяться умело с пользой
- 3. Дорогой друг! Сегодня у тебя необычный
- 4. ХОД УРОКА:Организационный момент.Актуализация опорных знаний.
- 5. УСТНО:1. Сравните числовые последовательности1). 1, 2, 4;
- 6. ТестВариант 11.Дописать пропущенное: «Числовая последовательность b1, b2,
- 7. ОТВЕТЫ ТЕСТАI – вариант1. bn+1 =
- 8. НАЗАД, В ИСТОРИЮ!На связь между прогрессиями первым
- 9. АНГЛИЯ XVIII ВЕКВ XVIII в. в английских учебниках появились обозначения арифметической и геометрической прогрессий:
- 10. Сведения, связанные с прогрессиями, впервые встречаются в
- 11. ДРЕВНИЙ ЕГИПЕТ
- 12. ГЕРМАНИЯНашел моментально сумму всех натуральных чисел от
- 13. Шахматная игра была придумана в
- 14. -Я достаточно богат, чтобы исполнить
- 15. Когда на другой день Сета снова
- 16. -Довольно, - с раздражением прервал
- 17. Почему так хитро улыбнулся Сета? Прав
- 18. Тема урока:Формула суммы n первых членов геометрической прогрессии
- 19. Выведем теперь формулу суммы n
- 20. За обедом царь вспомнил об
- 21. Утром царю доложили, что старшина придворных
- 22. -Как бы велико оно ни
- 23. С изумлением внимал царь
- 24. -Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот
- 25. Такова легенда. Действительно ли было
- 26. S = 264 – 1
- 27. ВЫВОДЕсли бы царю удалось засеять пшеницей площадь
- 28. Не в количестве знаний заключается образование,
- 29. В благоприятных условиях бактерии размножаются так,
- 30. Приходит как-то раз к одному богатому
- 31. План исследованияВычислить сумму, которую получит купецУзнать сумму, которую получит мужикСравнить доходыСделать выводы
- 32. Сумма, которую получит купецSкупец= 100000руб х 30дней = =3000000руб
- 33. Сумма, которую получит мужик1-ый день- 1коп2-ой
- 34. Последовательность чисел 1; 2; 4; 8;
- 35. Дано: геометрическая прогрессия b1=1 q=2Найти:S30Решение:
- 36. Сравним доходыкупец получил 3 000 000 рубмужик
- 37. ПРОВЕРЬ СЕБЯ1 вариантОбязательная часть.Дана геометрическая прогрессияb1= -
- 38. SN =S5 =S6 =1 вариант2 вариант
- 39. Sn =1 вариант2 вариантS5 =S6 =
- 40. ВАШЕ НАСТРОЕНИЕ
- 41. узнал…научился…понял, что…смог …могу научить…Сегодя Подошёл к концу
- 42. спасибо за работу Домашнее задание:П. 18, выучить
Слайд 2Математические знания могут применяться умело с пользой лишь в том случае,
Слайд 3Дорогой друг!
Сегодня у тебя необычный урок математики. Сегодня ты
Желаю тебе успехов и творческих радостей на уроке!
Слайд 4ХОД УРОКА:
Организационный момент.
Актуализация опорных знаний.
Проверка домашнего задания
Устная работа (5 мин.).
Проверочный тест (5 мин.).
Историческая справка (5 мин.).
Изучение новой темы (10 мин.).
Исторические задачи (5 мин.).
Задачи на закрепление новой темы (5 мин.).
Домашнее задание (2 мин.).
Рефлексия (2 мин.).
Выставление оценок (5 мин.).
Слайд 5УСТНО:
1. Сравните числовые последовательности
1). 1, 2, 4; -8 …
2). 1; -2;
3). 1; -2; -4; -8 …
4). 1, 2, 4, 8 …
Найдите закономерности. .
Какие из приведенных последовательностей являются геометрической прогрессией?
2. Сравните числовые последовательности
1). 2,3; 3,5; 4,7; 5,9 …
2). -8; 1; -2; 4 …
3). 3; -9; 27; 81 …
4). 3; 5; 7; 9 …
Есть ли здесь арифметическая прогрессия?
Есть ли среди них геометрическая прогрессия?
3. Является ли число 1/4геометрической прогрессией 8; 4; 2 ..? Если да, то укажите номер.
.
Слайд 6Тест
Вариант 1
1.Дописать пропущенное: «Числовая последовательность b1, b2, b3, .... bn, ....
где b1 ≠ 0, g ≠ 0
2 Написать формулу n - члена геометрической прогрессии.
3. Является ли геометрической прогрессией последовательность; 5, 25, 125, ..?
Назовите следующий член прогрессии.
4.(bn) - геометрическая прогрессия, b1 = 16, g = 1/2. Найдите b2, b3, b4.
5.(bn) - геометрическая прогрессия, b6 = 1/27, g = 1/3, Найдите b1.
Вариант 2
1. Дописать пропущенное: «Знаменателем геометрической прогрессии bп называется число g, которое вычисляется по формуле....... . »
2. Написать формулу n-го члена геометрической прогрессии.
3. Является ли геометрической прогрессией последовательность: 36, 18, 9,…?
Назовите следующий член прогрессии.
4.(bn) - геометрическая прогрессия, b1 = 1, g = 2. Найдите b2, b3, b4
5.(bn) — геометрическая прогрессия. b5=1/64, g = 1/2: Найдите b1.
Слайд 7ОТВЕТЫ ТЕСТА
I – вариант
1. bn+1 = b1qn где b1 ≠
2. b n = b1 *qⁿ-1
3. Да , 625
4. b1 = 16, b2= 16*1/2 = 8,
b3= 8 *1/2 =4, b4 = 4 *1/2= 2
5. bn= b1 qn-1, b1 = bn /qn-1,
b1= 1/27:(1/3)5= 1/27* 35 = 32 =9
II – вариант:
1. q =b2 / b1 = bn-1 / bn
2. b n = b1 *qⁿ-1
3. Да. 4,5
4. b2 = 1 * 2= 2 ; b3 = 2 * 2= 4 ; b4 = 4 * 2= 8
5. b1 = b5 /q4; b1 =1/64:(1/2)4 = 1/ 26 * 24 = 1/4
Слайд 8НАЗАД, В ИСТОРИЮ!
На связь между прогрессиями первым обратил внимание великий АРХИМЕД
Термин “прогрессия” был введен римским автором Боэцием (в 6 веке) и понимался в более широком смысле, как бесконечная числовая последовательность. Названия “арифметическая” и “геометрическая” были перенесены из теории непрерывных пропорций, которыми занимались древние греки.
Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (в 3 веке). Формула суммы членов геометрической прогрессии дана в книге Евклида “Начала” (3 век до н.э.).
Правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книги абака» в 1202г. (ЛеонардоПизанский)
Понятие числовой последовательности возникло и развивалось задолго до создания учения о функциях.
Слайд 9АНГЛИЯ XVIII ВЕК
В XVIII в. в английских учебниках появились обозначения арифметической
Слайд 10Сведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах
Древняя Греция
Слайд 12ГЕРМАНИЯ
Нашел моментально сумму всех натуральных чисел от 1 до 100, будучи
1 + 2 + 3 + 4 + ….. + 99 + 100 = (1 + 100) + (2 + 99) + …… + (50 + 51) = 101 ∙ 50 = 5050
Решение
КАРЛ ГАУСС
(1777 – 1855)
Слайд 13
Шахматная игра была придумана в Индии, и когда индусский
Слайд 14 -Я достаточно богат, чтобы исполнить самое смелое твое пожелание,
Сета молчал.
-Не робей, - ободрил его царь. – Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его.
-Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра я сообщу тебе мою просьбу.
-Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, -сказал царь.
Мудрец поклонился.
Слайд 15 Когда на другой день Сета снова явился к ступеням трона,
-Повелитель, - сказал Сета, - прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
-Простое пшеничное зерно? – изумился царь.
-Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью - 4, за четвертую - 8, за пятую - 16, за шестую -32…
Слайд 16 -Довольно, - с раздражением прервал его царь. – Ты
Сета улыбнулся хитро, покинул дворец и стал дожидаться у ворот дворца.
Слайд 17Почему так хитро улыбнулся Сета?
Прав ли был индусский царь,
Об этом ты узнаешь чуточку позже.
Слайд 19
Выведем теперь формулу суммы n первых членов произвольной геометрической
Воспользуемся тем же приемом, с помощью которого была вычислена сумма в задаче№1. Пусть дана геометрическая прогрессия (bn). Обозначим сумму n первых ее членов через Sn:
Sn = b1 + b2 + b3 +………+bn-1 + bn. (1)
Умножим обе части этого равенства на q: Sn ·q = b1· q + b2 ·q + d3· q +…..+bn· q
Учитывая, что b1· q = b2, b2· q = b3,……bn-1· q = bn,
получим: Sn·q = b2 + b3 + b4+ ……+ bn + bn·q (2)
Вычтем почленно из (2) равенство (1) и приведем подобные члены : Sn·q – Sn = (b2+b3+b4+….+bn+bn·q) – (b1+b2+b3+…..+bn) = bn·q – b1 ⇒ Sn(q – 1) = bn·q – b1
Sn = (bn·q – b1) / (q – 1)
Sn =
Слайд 20 За обедом царь вспомнил об изобретателе шахмат и послал
-Повелитель, - был ответ, - приказание твое исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился. Он не привык, чтобы повеления его исполнялись так медлительно.
Вечером, отходя ко сну, царь еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
-Повелитель, - ответили ему, - математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.
Слайд 21 Утром царю доложили, что старшина придворных математиков просит выслушать важное
Царь приказал ввести его.
-Прежде чем скажешь о твоем деле, - объявил Шерам, - я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.
-Ради этого я и осмелился явиться перед тобой в столь ранний час, - ответил старик. – Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…..
Слайд 22 -Как бы велико оно ни было, - надменно перебил
- Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, которое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни.
Слайд 23
С изумлением внимал царь словам старца.
Пусть все пространство их будет сплошь засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду…
Слайд 24-Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят
18 446 744 073 709 551 615
Слайд 25 Такова легенда. Действительно ли было то, что здесь рассказано,
Фактически, число зерен, о которых идет речь, является суммой 64 членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:
S = 1+2+22+23+24+…….+262+263
Слайд 26 S = 264 – 1
Значит, подсчет зерен сводится
=1024 · 1024 ·1024· 1024 ·1024· 1024· 16 =
=1048576 ·1048576 ·1048576 ·16 – 1
и получим искомое число зерен:
18 446 744 073 709 551 615
Масса такого числа зерен больше триллиона тонн.
Индусский царь не в состоянии был выдать подобной награды.
Но будь он силен в математике, он бы не попал впросак…
Слайд 27ВЫВОД
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая
Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до настоящего времени.
Слайд 28
Не в количестве знаний заключается
образование, а в полном понимании
что знаешь.
Георг Гегель
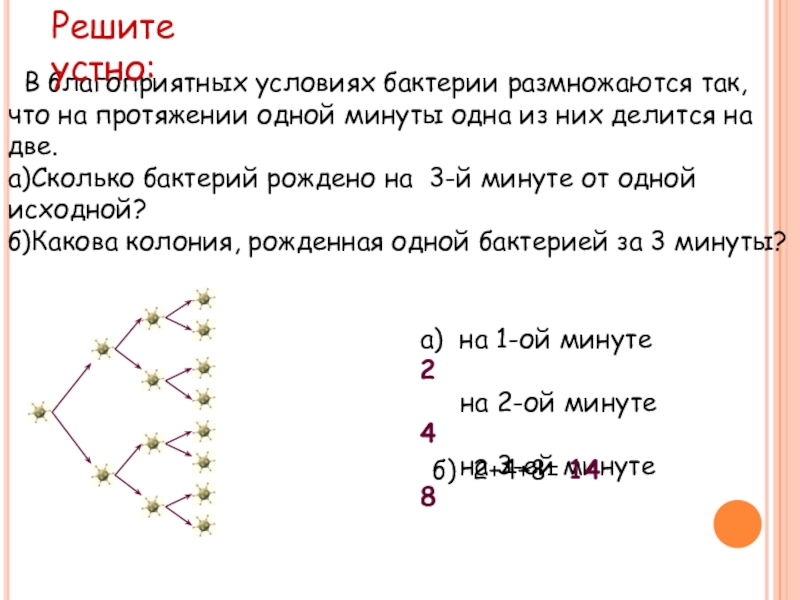
Слайд 29 В благоприятных условиях бактерии размножаются так,
что на протяжении одной
а)Сколько бактерий рождено на 3-й минуте от одной исходной?
б)Какова колония, рожденная одной бактерией за 3 минуты?
а) на 1-ой минуте 2
на 2-ой минуте 4
на 3-ей минуте 8
б) 2+4+8= 14
Решите устно:
Слайд 30 Приходит как-то раз к одному богатому
купцу мужик и
«Давай, говорит, в течение месяца я
буду приносить тебе каждое утро по
100000 руб, а ты мне взамен в первый
день отдашь 1 коп, а в каждый последую-
щий в 2 раза больше. Во второй день-
2 коп, в третий- 4 коп и т.д.»
Подумал купец и подписал договор.
Кому выгодна сделка?
Слайд 31План исследования
Вычислить сумму, которую получит купец
Узнать сумму, которую получит мужик
Сравнить доходы
Сделать
Слайд 33Сумма, которую получит мужик
1-ый день- 1коп
2-ой день- 2коп
3-ий день-
4-ый день- 8коп
5-ый день- 16коп
6-ой день- 32коп
7-ой день- 64коп
8-ой день- 128коп
9-ый день-256 коп
10-ый день- 512 коп
11-ый день- 1024 коп
12-ый день- 2048 коп
13-ый день- 4096 коп
14-ый день- 8192 коп
15-ый день- 16384 коп
……………………………
Путь не рациональный.
Замечаем, что каждая
последующая выплата
в 2 раза больше предыдущей.
Слайд 34 Последовательность чисел 1; 2; 4; 8; 16;…
представляет собой геометрическую прогрессию,
у которой b1=1, q=2.
Следовательно, необходимо найти сумму первых
30 членов данной геометрической прогрессии.
Вывод
каким образом???
Слайд 35Дано:
геометрическая прогрессия
b1=1
q=2
Найти:
S30
Решение:
S30= = 230 -1 = 1073741824 -1 =
= 1073741823 коп = 10737418 руб 23 коп
Сумма, которую получит мужик
Слайд 36Сравним доходы
купец получил 3 000 000 руб
мужик – 10 737 418
разница составляет 7 737 418 РУБ 23 КОП !!!
Так кому выгодна эта сделка?
Слайд 37ПРОВЕРЬ СЕБЯ
1 вариант
Обязательная часть.
Дана геометрическая прогрессия
b1= - 4, q=2. Найти S5
b1=4, b2=16. Найти S6
Дополнительная часть.
3) Упростите выражение, применив формулу суммы n первых членов геометрической прогрессии:
1+х+х2+х3+х4=
х≠1
2 вариант
Обязательная часть.
Дана геометрическая прогрессия
b1= - 9, q=2. Найти S6
b1=3, b2=9. Найти S5
Дополнительная часть.
3) Упростите выражение, применив формулу суммы n первых членов геометрической
прогрессии:
1+х+х2+х3+х4 +х5=
х≠1
Слайд 41узнал…
научился…
понял, что…
смог …
могу научить…
Сегодя
Подошёл к концу наш урок. Давайте подведем
У вас у каждого на парте лежат смайлики, поднимите, пожалуйста, тот, который расскажет о вашем настроении после урока, о впечатлении от урока. Кто из вас выскажет мнение о пройденном уроке, вот фразы, с которых вы можете начать…
Рефлексия
Слайд 42спасибо за работу
Домашнее задание:
П. 18, выучить формулы
Задача 1
Некто продавал коня
Задача 2
Придумать задачу на применение формулы суммы геометрической прогрессии.