- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры методы решения тригонометрических уравнений .
Содержание
- 1. Презентация к уроку алгебры методы решения тригонометрических уравнений .
- 2. Слайд 2
- 3. ТЕМА УРОКА : Методы
- 4. Устная работа 1. Вычислите а) arсsin1/2 =
- 5. Вычислитеа) arсsin 1/2 = П/6
- 6. Вычислитеа) arсsin 1/2 = П/6б) arсsin (- 1/2 ) =
- 7. Вычислитеа) arсsin 1/2 = П/6б) arсsin (- 1/2 ) = -П/6
- 8. Вычислитеа) arсsin 1/2 = П/6б) arсsin (- 1/2 ) = - П/6в) arccos √3/2=
- 9. Вычислитеа) arсsin 1/2 = П/6б) arсsin (- 1/2 ) = - П/6в) arccos √3/2= П/6
- 10. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 11. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 12. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 13. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 14. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 15. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 16. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 17. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 18. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 19. Вычислитеа) arсsin 1/2 = П/6б) arсsin (-
- 20. Найдите ошибку и исправьте ее. а) cos х
- 21. Найдите ошибку и исправьте ее.а) cos х
- 22. Найдите ошибку и исправьте ее. б) sin х
- 23. Найди ошибку и исправь ееб) sin х
- 24. Найдите ошибку и исправьте ееб) sin х
- 25. Самостоятельная работа по вариантам на карточках Решите
- 26. Взаимопроверка 1 вариант ∙ 1)sin х
- 27. Установите соответствие.( Работа в парах)Установите соответствие между
- 28. Установите соответствие.( Работа в парах)Установите соответствие между
- 29. Практикум по решению тригонометрических уравнений( работа в
- 30. Повторение 1)5 sin2 x – 14Sinxcosx
- 31. Алгоритм решения однородного тригонометрического уравнения первой
- 32. Алгоритм решения однородного тригонометрического уравнения второй
- 33. Практикум по решению уравнений. Работа в
- 34. Решение уравнений. Коллективная работа
- 35. Решение уравнений. Коллективная работа
- 36. 7. Дифференцированная самостоятельная работа На выбор
- 37. Домашнее задание Задачник Алгебра и начала анализа
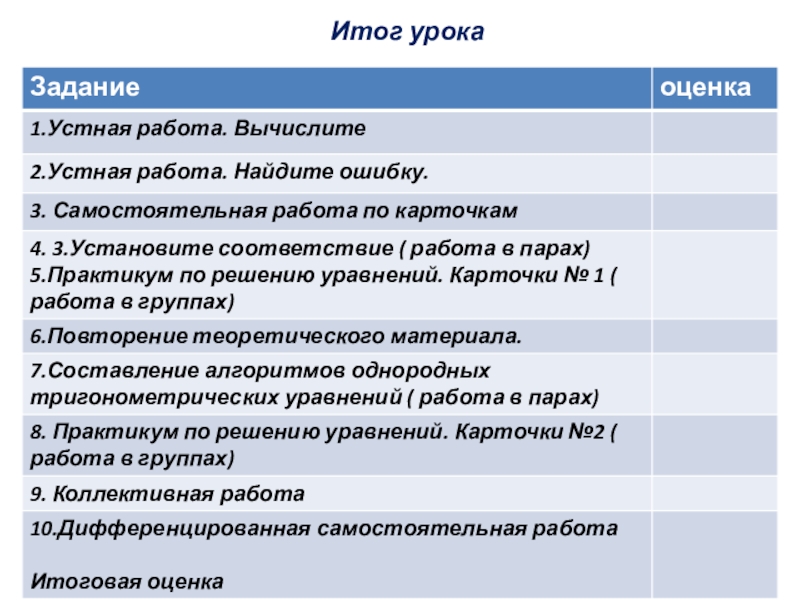
- 38. Итог урока
- 39. Рефлексия На уроке я…-Узнал…Понял…Научился…Самый большой мой успех
- 40. Спасибо за урок !
- 41. Использовалась литература :1 Мордкович А.Г., Семенов
Слайд 1Методы решения тригонометрических уравнений
Учитель математики МАОУ Богандинской СОШ № 42
Слайд 3 ТЕМА УРОКА : Методы решения тригонометрических уравнений. Цель урока: Формирование умений
цц
Слайд 10Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )=
Слайд 11Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= 5П/6
Слайд 12Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= 5П/6
д) arctg 1 =
Слайд 13Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= П/6
д) асtg 1 = П/4
Слайд 14Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= 5П/6
д) arctg 1 = П/4
е) arctg ( -1 ) =
Слайд 15Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= 5П/6
д) tg 1 = П/4
е) tg ( -1 ) = - П/4
Слайд 16Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= 5П/6
д) arctg 1 = П/4
е) arctg ( -1 ) = - П/4
ж) arcсtg 1 =
Слайд 17Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= 5П/6
д) arctg 1 = П/4
е) arctg ( -1 ) = - П/4
ж) arcсtg 1 = П/4
Слайд 18Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= 5П/6
д) arctg 1 = П/4
е) arctg ( -1 ) = - П/4
ж) arcсtg 1 = П/4
з) arcсtg ( - 1 ) =
Слайд 19Вычислите
а) arсsin 1/2 = П/6
б) arсsin (- 1/2 ) = -
в) arccos √3/2= П/6
г) arccos (– √3/2 )= 5П/6
д) arctg 1 = П/4
е) arctg( -1 ) = - П/4
ж) arcсtg 1 = П/4
з) arcсtg ( - 1 ) = 3П/4
Слайд 20Найдите ошибку и исправьте ее.
а) cos х = а, Х =
б) sin х = a,
в) tg х = a, х = arctga + πn, n € Z
Слайд 21Найдите ошибку и исправьте ее.
а) cos х = а, Х =
Если │а │≤ 1, то Х = ± arccos a + 2πn, n € Z
Слайд 24Найдите ошибку и исправьте ее
б) sin х = a
sin х
если │а │≤ 1, то Х= (-1)k arсsin а +πk, k € Z
или Х = arсsin а + 2πk, k € Z
Х = (П- arсsin а) + 2πk, k € Z
Слайд 25Самостоятельная работа по вариантам на карточках
Решите уравнения
1 вариант
1)sin х = 0 1) cos x = 0
2) sin х = 1 2) cos x = 1
3) sin х = -1 3) cos x = - 1
4) ctg x = 1 4) tg x = 1
5) ctg x = - 1 5) tg x = - 1
Слайд 26Взаимопроверка
1 вариант
∙ 1)sin х = 0, x =
2) sin х = 1, x = П/2 + 2Пn, n €Z
3) sin х = -1, x = - П/2 + 2Пn, n €Z
4) ctg x = 1, x = П/4 +Пn, n €Z
5) ctg x = - 1, x = 3/4 ∙П +Пn, n €Z
2 вариант
1) cos x = 0, x = П/2 + Пn, n €Z
2) cos x = 1, x = 2Пn, n €Z
3) cos x = - 1 , x = П + 2Пn, n €Z
tg x = 1, x = П/4 +Пn, n €Z
tg x = - 1, x = - П/4 +Пn, n €Z
Слайд 27Установите соответствие.( Работа в парах)
Установите соответствие между уравнениями и возможными решениями:
Уравнения Решения
а) Sin x = - 1/2 1).x = П/6 + 2Пn, x = - П/6 + 2Пn, n €Z
б) cos x = √3/2 2)х = - П/6 + 2Пn, x = - 5/6П + 2Пn, n €Z
в) tg x =√3 3). x = 3/4П + 2Пn, x = - 3/4П + 2Пn, n €Z
г) cоs x = - √2/2 4). Х = П/3 + Пn, n €Z .
Слайд 28Установите соответствие.( Работа в парах)
Установите соответствие между уравнениями и возможными решениями:
Уравнения Решения
а) Sin x = - 1/2 1).x = П/6 + 2Пn, x = - П/6 + 2Пn, n €Z
б) cos x = √3/2 2)х = - П/6 + 2Пn, x = - 5/6П + 2Пn, n €Z
в) tg x= √3 3). x = 3/4П + 2Пn, x = - 3/4П + 2Пn, n €Z
г) cоs x = - √2/2 4). Х = П/3 + Пn, n €Z .
Слайд 29Практикум по решению тригонометрических уравнений( работа в группах) Карточки №1.
Проанализируйте решение
Решите уравнение1, работая в группе.
Слайд 30Повторение
1)5 sin2 x – 14Sinxcosx - 3 cos2x =
2)2 cos2 3х – 5cos3x – 3 = 0,
3) 6sin х + 7cos х = 0,
4) sin2 x = 3 cos2x - 2sinxcosx
a)Назовите однородные тригонометрические уравнения первой степени
б)Дайте определение однородного тригонометрического уравнения первой степени
в)Назовите однородные тригонометрические уравнения второй степени
г)Дайте определение однородного тригонометрического уравнения второй степени
Слайд 31Алгоритм решения однородного тригонометрического уравнения первой степени, т. е. уравнения вида
1.Делим обе части уравнения на cos x ≠ 0
( если cos x = 0, то и sin x=0, что невозможно т.к. cos2x + sin2 x = 1)
2. Приходим к простейшему уравнению
tg x = - в/а
Слайд 32Алгоритм решения однородного тригонометрического уравнения второй степени, т. е. уравнения вида а
1.Посмотрим, есть ли в уравнении член а sin2 x
2.Если член а sin2 x в уравнении содержится
(т.е. а ≠ 0 ), то уравнение решается делением обеих частей на cos2x ≠ 0 и последующим введением новой переменной tg x= у.
3. Если член а sin2 x в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносится cos х
Слайд 33Практикум
по решению уравнений. Работа в группах
Решить уравнения
1) sin2 x – 5Sinx cosx + 6cos2x = 0,
2) sin2 4х– 2Sin 4x cos 4x = 0.
Карточка №2 ( 2 группа)
Решить уравнения
1) 3sin2 3х + 10Sin3x cos3x + 3cos23х= 0,
2) 5 cos2x + 4Sin x cos x - cos2x = 0.
Карточка №2 ( 3 группа)
Решить уравнение
1) 3sin2 х + Sinx cosx - 2cos2х= 0,
2)2 sin2 x = 3cos2x .
Слайд 34Решение уравнений. Коллективная работа
Задачник .Мордкович А.Г., Семенов
Решить уравнение
5sin2 x – 14Sinx cosx - 3cos2x = 2
Чем это уравнение сложнее предыдущих?
Решим это уравнение у доски и в тетрадях.
Слайд 35Решение уравнений. Коллективная работа
Задачник Алгебра и начала анализа 10 класс . Профильный уровень . Стр.134 №23.18 (а)
Решить уравнение
5sin2 x – 14Sinx cosx - 3cos2x = 2
Ответ: arctg5 + Пn, n €Z, arctg 1/3+ Пn, n €Z,
Слайд 367. Дифференцированная самостоятельная работа
На выбор учащихся предлагается 3 варианта:
А
Вариант А Вариант В
1)сosx = √3/2 ; 1) 2sin2 х - 3 cosx = 0; 2) (2sin x – 1)(tg x - 1 ) = 0 2) tg2 x – 3 tg x + 2 = 0. Вариант С
1)8 sin2 х + cosx + 1 = 0;
2) 4 sin 2х + 3 sin x cos x - cos2 x = 0.
Слайд 37Домашнее задание
Задачник Алгебра и начала анализа 10 класс . Профильный
№23.16 ; № 23.12; №23.2 (г,д)- обязательный минимум.
Дополнительно №23.18(г)
Слайд 39Рефлексия
На уроке я…
-Узнал…
Понял…
Научился…
Самый большой мой успех – это…
Я не умел,
- Я изменил свое отношение к …
Слайд 41 Использовалась литература
:
1 Мордкович А.Г., Семенов П.В. Алгебра и начала математического
2 Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа. 10 класс. Часть 2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) 10-е изд. М: Мнемозина, 2013
3.Л.А. Александрова ; Алгебра и начала математического анализа. 10 класс. Самостоятельные работы для учащихся общеобразовательных учреждений (профильный уровень) под ред. А.Г.Мордковича – М. : Мнемозина, 2012. – 207 с.: ил.
34.И.В. Фотина . Математика .5-11 классы. Коллективный способ обучения: конспекты уроков, занимательные задачи. Волгоград : Учитель, 2009.
В.И. Садкина 101 педагогическая идея как создать урок. 2-е изд. – Ростов н/Д: Феникс, 2015. -87.с. – (Золотая педагогическая коллкция)