- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры Методы решения логарифмических уравнений (10-11 класс)
Содержание
- 1. Презентация к уроку алгебры Методы решения логарифмических уравнений (10-11 класс)
- 2. Логарифм и ОДЗLoga b=Х ах =bЛогарифм и ОДЗВМЕСТЕтрудятсявезде!b?a?
- 3. Устный счет-2=1/2927lg 0,1=-1не существует42+log45 =803-2
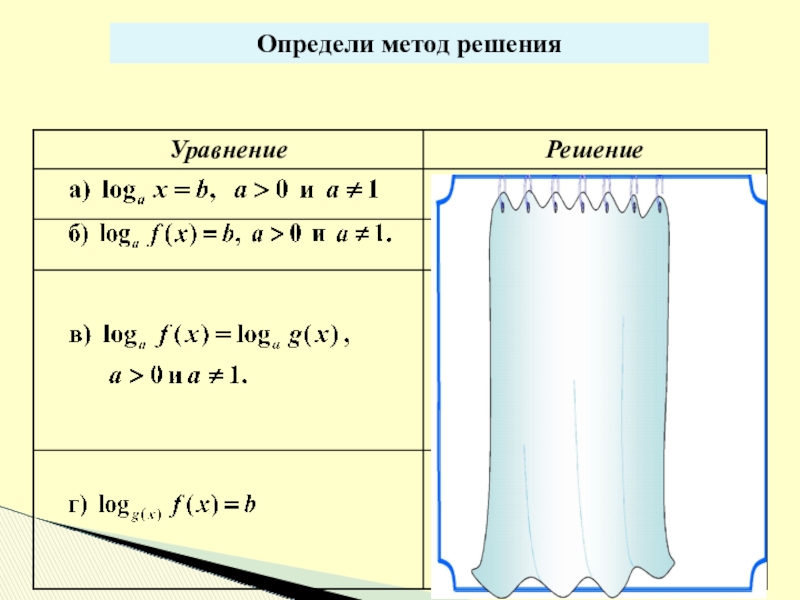
- 4. Определи метод решения
- 5. Слайд 5
- 6. Решите уравненияX=24X=-10 и X=10X=16Гимназия № 8 Сочиx=64log2x+4log4x=12xlgx=100x;Работа в парах. Решите уравнения.
- 7. Проблема?
- 8. Первичное закрепление
- 9. Физминутка
- 10. Слайд 10
- 11. Самостоятельная работаxlgx=x100; x0,5lgx=0,01x2; X2log3x=3log33xРешите уравнения методом логарифмирования
- 12. Самопроверкаxlgx=x100; 1)ОДЗ: х>02) lgxlgx=lgx100;lg2x = 100lgxlg2x -
- 13. Решение систем логарифмических уравнений№ 521 (а,б,в)
- 14. Домашнее заданиеП.39№521 (г)№ 522 (б,в)№ 523 (в)
- 15. Спасибо за работу на уроке!
Логарифм и ОДЗLoga b=Х ах =bЛогарифм и ОДЗВМЕСТЕтрудятсявезде!b?a?
Слайд 6Решите уравнения
X=24
X=-10 и X=10
X=16
Гимназия № 8
Сочи
x=64
log2x+4log4x=12
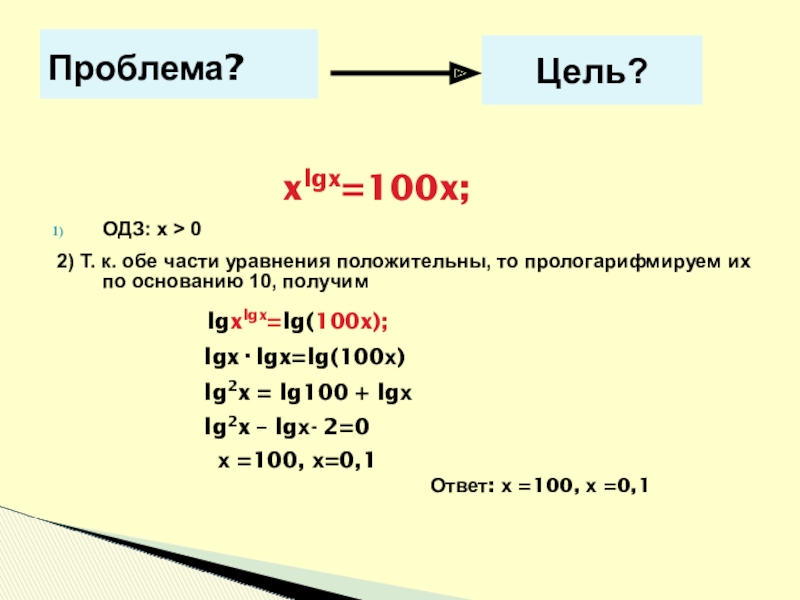
xlgx=100x;
Работа в парах. Решите
уравнения.
Слайд 7Проблема?
xlgx=100x;
ОДЗ: х > 0
2) Т. к. обе части уравнения положительны, то прологарифмируем их по основанию 10, получим
lgxlgx=lg(100x);
lgx·lgx=lg(100х)
lg2x = lg100 + lgх
lg2x – lgх- 2=0
х =100, х=0,1
Ответ: х =100, х =0,1
ОДЗ: х > 0
2) Т. к. обе части уравнения положительны, то прологарифмируем их по основанию 10, получим
lgxlgx=lg(100x);
lgx·lgx=lg(100х)
lg2x = lg100 + lgх
lg2x – lgх- 2=0
х =100, х=0,1
Ответ: х =100, х =0,1
Цель?
Слайд 8Первичное закрепление
Xlgx+2 = 1000
1)ОДЗ: Х>0
2) Т. к. обе части уравнения положительны, то логарифмируя их по основанию 10, получим:
lgxlgx+2 = lg1000
( lgx+2)·lgx=lg1000
lg2x+ 2lgx- 3=0
lgx=y
у2 + 2у- 3=0
y=- 3, у=1.
lgx=- 3, x=10-3=0,001;
lgx=1, x=10
Ответ: 0,001; 10.
1)ОДЗ: Х>0
2) Т. к. обе части уравнения положительны, то логарифмируя их по основанию 10, получим:
lgxlgx+2 = lg1000
( lgx+2)·lgx=lg1000
lg2x+ 2lgx- 3=0
lgx=y
у2 + 2у- 3=0
y=- 3, у=1.
lgx=- 3, x=10-3=0,001;
lgx=1, x=10
Ответ: 0,001; 10.
Слайд 11Самостоятельная работа
xlgx=x100;
x0,5lgx=0,01x2;
X2log3x=3log33x
Решите уравнения методом логарифмирования
Слайд 12Самопроверка
xlgx=x100;
1)ОДЗ: х>0
2) lgxlgx=lgx100;
lg2x = 100lgx
lg2x - 100lgx =0
lgx(lgx – 100)
=0
lgx =0 или
lgx = 100
х =1 или х =10100
Ответ: х=1, х=10100
lgx =0 или
lgx = 100
х =1 или х =10100
Ответ: х=1, х=10100
x0,5lgx=0,01x2;
1)ОДЗ: х>0
2) lgx0,5lgx=lg0,01x2;
0,5lgxlgx – (-2+2lgx)=0
0,5lg2x - 2lgx+2=0
lg2x - 4lgx +4 =0
(lgx -2)2=0
lgx =2
х=100
Ответ: х=100
X2log3x=3log33x
1)ОДЗ:х>0
2) log3X2log3x=log33log33x
2log3x·log3x=log3(3x)·log33
2log32x = 1+log3x
2log32x -1-log3x=0
X=3 или х=3-0,5
Ответ: х=3,
х=3-0,5