- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры
Содержание
- 1. Презентация к уроку алгебры
- 2. В подборке представлены задачи с реальным содержанием:
- 3. 1 Задачи из обиходной жизни
- 4. Задача 1В каком месте незастроенного треугольного двора
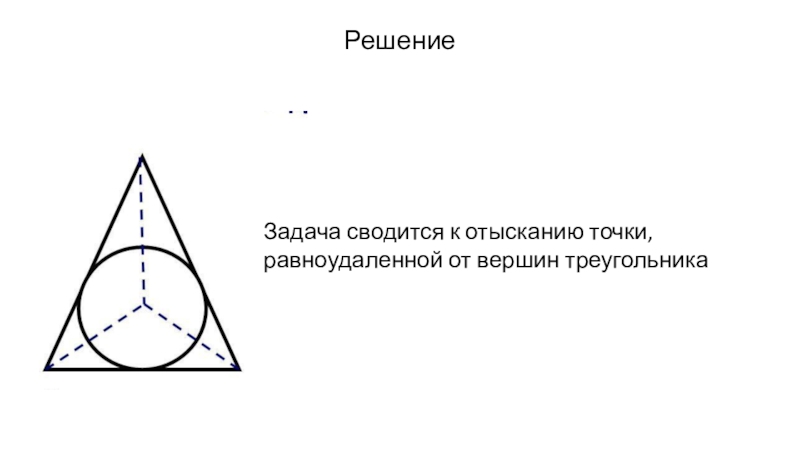
- 5. РешениеЗадача сводится к отысканию точки, равноудаленной от вершин треугольника
- 6. Задача 2Желая проверить, имеет ли отрезанный кусок
- 7. РешениеНет, недостаточна. Указанный прием убеждает лишь в
- 8. Задача 3Стакан вплотную обставлен соприкасающимися с ним и между собой стаканами такой же величины. Сколько их?
- 9. РешениеИз рисунка видно, что прямые, соединяющие центры
- 10. Задача 4Во сколько раз объем мясистой части
- 11. РешениеТак как диаметр вишни втрое больше диаметра
- 12. Задача 5Какие яйца выгоднее покупать: 60-миллиметровые(по длине) по 1 руб., или 55-миллиметровые по 75 коп.?
- 13. РешениеОбъем меньшего яйца (то есть колличество питательных
- 14. 2. Задачи из техники и сельского хозяйства
- 15. Задача 6Жестяники и столяры нередко пользуются следующим
- 16. РешениеДлина окружности получается при этом равной6r+(r-r √¯2/2)=
- 17. 3. Задачи из мироведения
- 18. Задача 7Вообразим, что земной шар вытянут в
- 19. РешениеОтвет- для большинства неожиданный- получается из уравнения1/4πx²
- 20. Задача 8Два котла, большой и малый, одинакового
- 21. РешениеВещи остывают с поверхности, следовательно , остынет
- 22. 4 Задачи из живой природы
- 23. Задача 9При каждом ударе сердце человека выталкивает
- 24. РешениеИскомое ребро куба обозначим через х. Тогдах³ = 75 · 60 · 24 · 175х=260 см
- 25. Задача 10Зрачок человеческого глаза может изменять свой
- 26. РешениеКоличество пропускаемого света пропорционально площади отверстия. Следовательно,
- 27. 5. Историческая задача
- 28. Задача 11Чтобы построить прямой угол на местности,
- 29. РешениеПолучался, так как выполняются равенства5²+12²=13² и 8²+15²=17²Прямой
- 30. Слайд 30
В подборке представлены задачи с реальным содержанием: из обиходной жизни, из техники, из мироведения, из живой природы и др. Выбор сюжетов и тем далеко не исчерпывает всех возможных вариантов, но дает общее представление о такого рода
Слайд 2В подборке представлены задачи с реальным содержанием: из обиходной жизни, из
техники, из мироведения, из живой природы и др. Выбор сюжетов и тем далеко не исчерпывает всех возможных вариантов, но дает общее представление о такого рода упражнениях. Последние послужат хорошими образцами для учителя, готового следовать по пути, предложенному когда-то Перельманом, желающего попробовать составлять такие задачи самостоятельно и привлекать к этому своих учеников, включая задачи данного вида в содержание уроков и внеурочных мероприятий.
Слайд 4Задача 1
В каком месте незастроенного треугольного двора нужно поместить фонарь, чтобы
все три угла двора были освещены им одинаково?
Слайд 6Задача 2
Желая проверить, имеет ли отрезанный кусок материи форму квадрата, швея
убеждается, что при перегибании по диагоналям края обеих частей совпадают. Достаточна ли такая проверка?
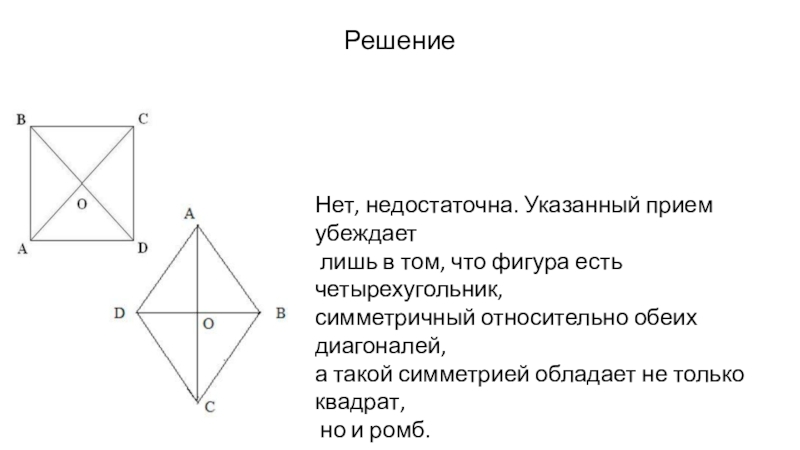
Слайд 7Решение
Нет, недостаточна. Указанный прием убеждает
лишь в том, что фигура есть
четырехугольник,
симметричный относительно обеих диагоналей,
а такой симметрией обладает не только квадрат,
но и ромб.
симметричный относительно обеих диагоналей,
а такой симметрией обладает не только квадрат,
но и ромб.
Слайд 8Задача 3
Стакан вплотную обставлен соприкасающимися с ним и между собой стаканами
такой же величины. Сколько их?
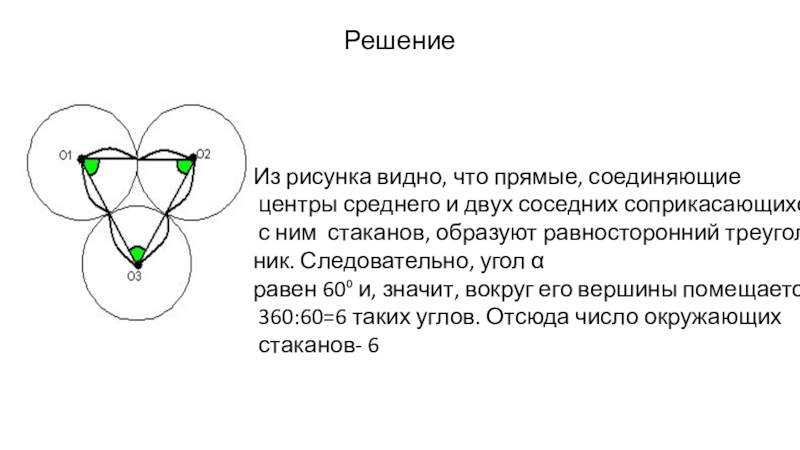
Слайд 9Решение
Из рисунка видно, что прямые, соединяющие
центры среднего и двух соседних
соприкасающихся
с ним стаканов, образуют равносторонний треуголь-
ник. Следовательно, угол α
равен 60⁰ и, значит, вокруг его вершины помещается
360:60=6 таких углов. Отсюда число окружающих
стаканов- 6
с ним стаканов, образуют равносторонний треуголь-
ник. Следовательно, угол α
равен 60⁰ и, значит, вокруг его вершины помещается
360:60=6 таких углов. Отсюда число окружающих
стаканов- 6
Слайд 10Задача 4
Во сколько раз объем мясистой части вишни больше объема косточки?
Толщину слоя мякоти принять равной ширине косточки
Слайд 11Решение
Так как диаметр вишни втрое больше диаметра косточки (то и другое
принимают за шары), то объем вишни больше объема косточки в 27 раз, а объем мякоти больше объема косточки в 26 раз. Значит, объем косточки составляет 1/26, то есть примерно 4% от объема мякоти
Слайд 12Задача 5
Какие яйца выгоднее покупать: 60-миллиметровые(по длине) по 1 руб., или
55-миллиметровые по 75 коп.?
Слайд 13Решение
Объем меньшего яйца (то есть колличество питательных веществ в нем), считая
форму обоих яиц одинаковой, меньше объема крупного яйца в отношении 55³ : 60³ ≈0,77. Следовательно меньшие яйца должны были бы продаваться по цене 77 коп, а не 75 коп. Более мелкие яйца покупать выгоднее.
Слайд 15Задача 6
Жестяники и столяры нередко пользуются следующим приемом для определения длины
окружности: откладывают на прямой 6 раз радиус данной окружности и прибавляют высоту меньшего сегмента, отрезаемого стороной вписанного в эту окружность квадрата. Оцените точность результата, который дает этот прием
Слайд 16Решение
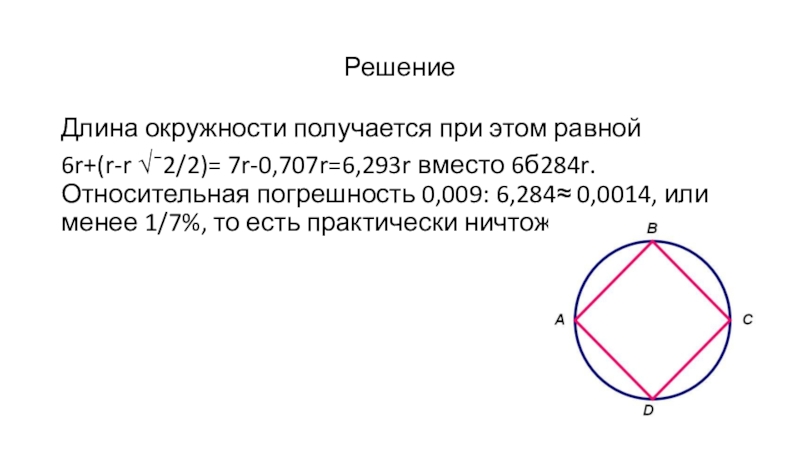
Длина окружности получается при этом равной
6r+(r-r √¯2/2)= 7r-0,707r=6,293r вместо 6б284r. Относительная
погрешность 0,009: 6,284≈ 0,0014, или менее 1/7%, то есть практически ничтожна.
Слайд 18Задача 7
Вообразим, что земной шар вытянут в цилиндрическую нить длиной от
Земли до Солнца. Какой толщины была бы эта нить?
Слайд 19Решение
Ответ- для большинства неожиданный- получается из уравнения
1/4πx² · 150 000 000=
1/6π · 12700³ , откуда x= 95,25 км.
Слайд 20Задача 8
Два котла, большой и малый, одинакового материала и формы (или
два самовара) наполнены кипятком. Какой остынет скорее?
Слайд 21Решение
Вещи остывают с поверхности, следовательно , остынет скорее тот котел, в
котором на каждую единицу объема приходится большая поверхность. Если один котел в n раз выше и шире другого, то поверхность его больше в n² раз, а объем-в n³ ; на единицу поверхности в большом котле приходится в n раз больший объем. Следовательно, меньший котел должен остыть раньше.
Слайд 23Задача 9
При каждом ударе сердце человека выталкивает 175 см³ крови. Сердце
делает 75 ударов в минуту. Каких размеров кубический сосуд потребовался бы, чтобы вместить количество крови, перекачиваемое сердцем в течении суток?
Слайд 25Задача 10
Зрачок человеческого глаза может изменять свой диаметр ( в зависимости
от яркости освещения) от 2 до 9 мм. Во сколько раз расширенный зрачок пропускает больше света, чем суженный?
Слайд 26Решение
Количество пропускаемого света пропорционально площади отверстия. Следовательно, расширенный зрачок пропускает больше
лучей, чем суженный, в отношении
9² / 2² = 81/4 ,то есть в 20,25 раз.
9² / 2² = 81/4 ,то есть в 20,25 раз.
Слайд 28Задача 11
Чтобы построить прямой угол на местности, древние индусы строили на
земле треугольник с соотношением сторон 5:12:13 или 8:15:17. Получался ли при этом прямой угол и если да, то против какой стороны?
Слайд 29Решение
Получался, так как выполняются равенства
5²+12²=13² и 8²+15²=17²
Прямой угол лежит против сторон
с длиной 13 и 17 единиц