- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку 11 класс Экстремумы функции
Содержание
- 1. Презентация к уроку 11 класс Экстремумы функции
- 2. Точки из области определения функции, в которых:
- 3. Точки из области
- 4. Пусть xо точка из области определения функции
- 5. Экстремумы функцииХ0 - точка максимума (max) функции,
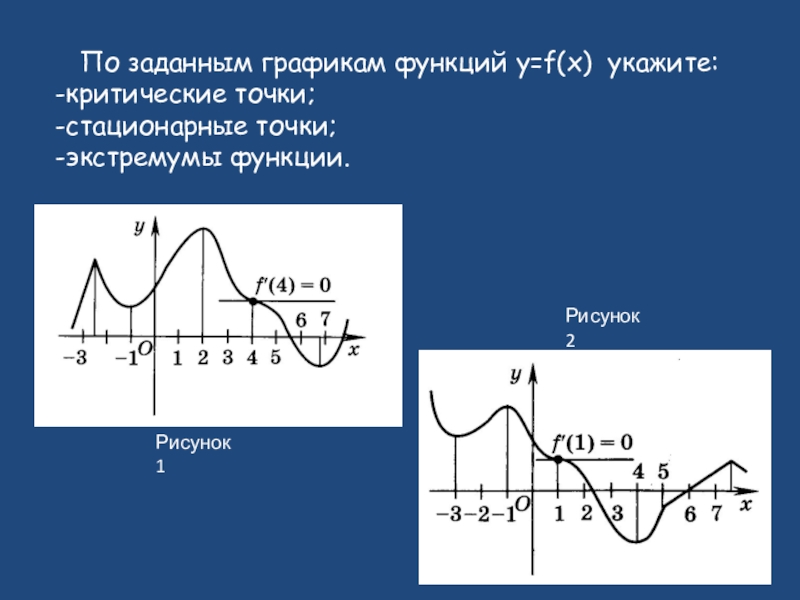
- 6. Рисунок 1Рисунок 2По заданным графикам функций y=f(x) укажите:-критические точки;-стационарные точки;-экстремумы функции.
- 7. Алгоритм поиска точек экстремума функции:1. Найти производную
- 8. Выполните задание1.Найдите точку максимума функции2.Наидите точку минимума функции
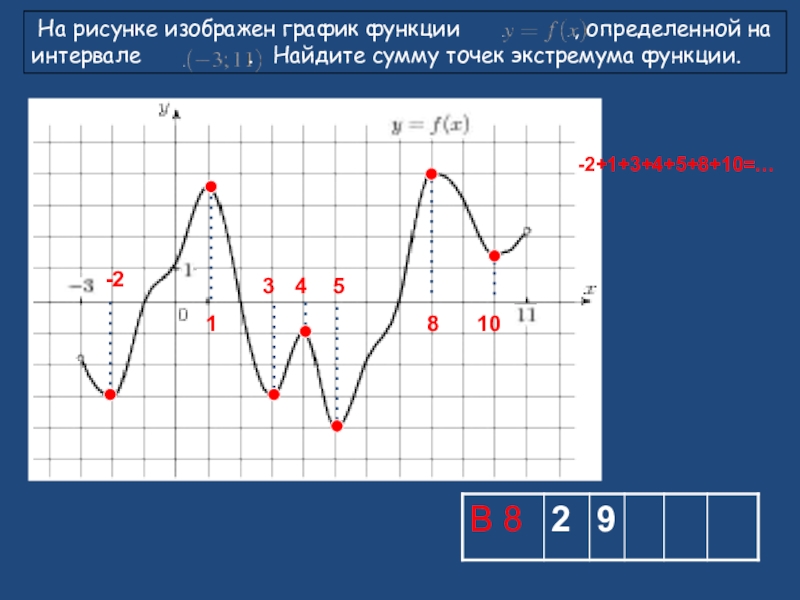
- 9. На рисунке изображен график функции
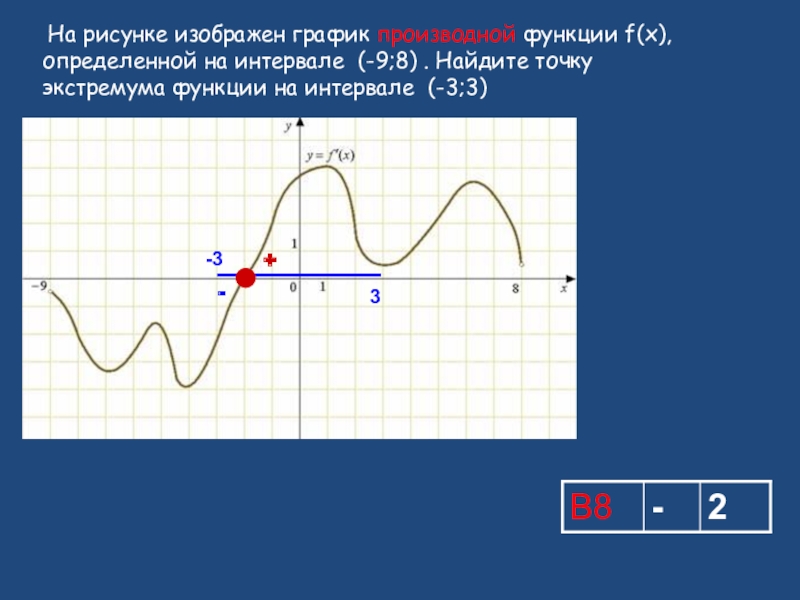
- 10. На рисунке изображен график производной функции f(x),
Точки из области определения функции, в которых: f′ (x) =0 или не существует, называются критическими точками этой функции. Только они могут быть точками экстремума функции. (рис. 1 и 2). f′ (x1) =0
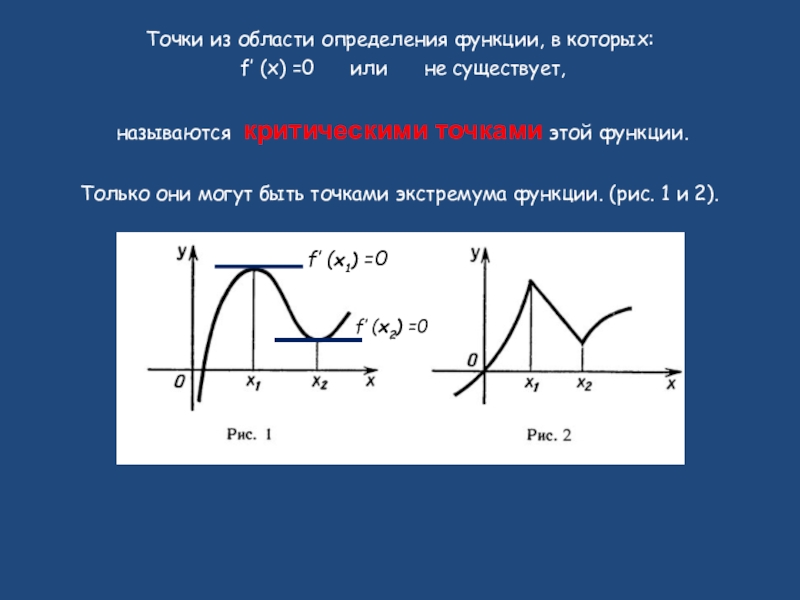
Слайд 2Точки из области определения функции, в которых:
f′ (x) =0
или не существует,
называются критическими точками этой функции.
Только они могут быть точками экстремума функции. (рис. 1 и 2).
называются критическими точками этой функции.
Только они могут быть точками экстремума функции. (рис. 1 и 2).
f′ (x1) =0
f′ (x2) =0
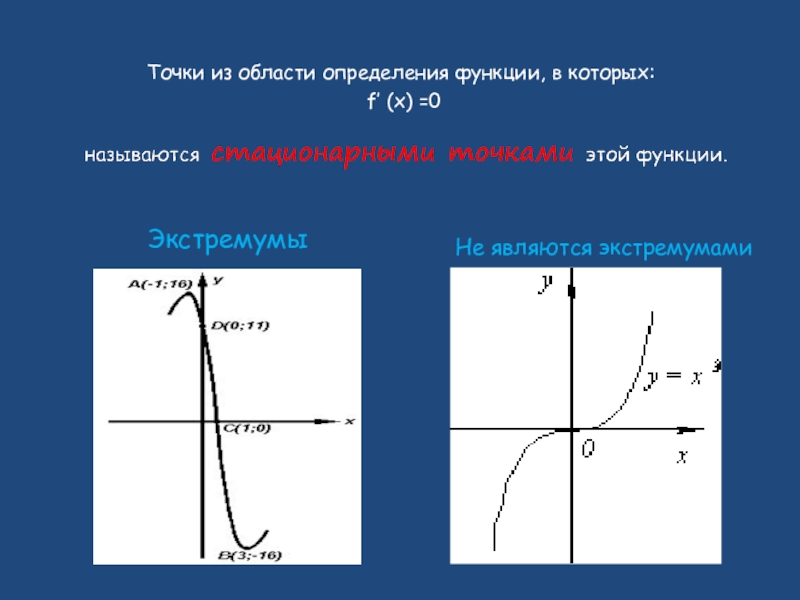
Слайд 3 Точки из области определения функции, в которых: f′ (x) =0
Экстремумы
Не являются экстремумами
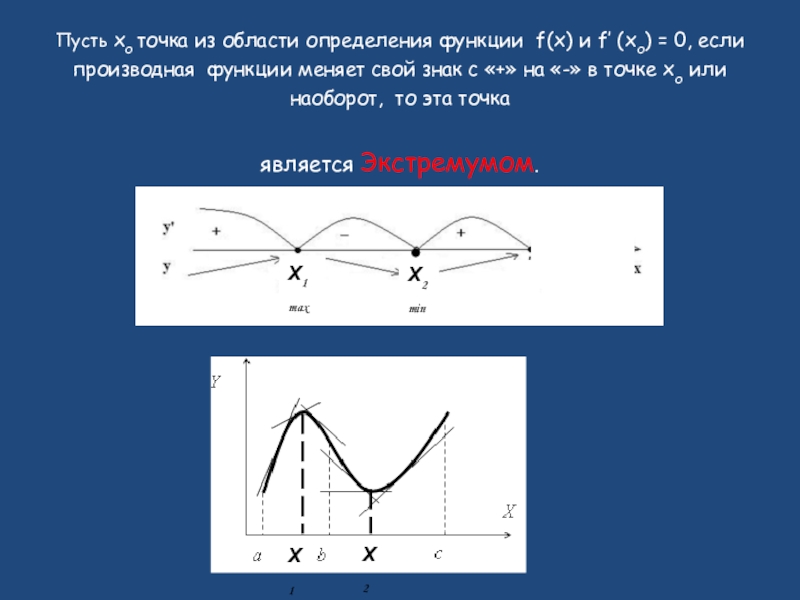
Слайд 4Пусть xо точка из области определения функции f(x) и f′ (xо)
= 0, если производная функции меняет свой знак с «+» на «-» в точке xо или наоборот, то эта точка
является Экстремумом.
Х1
max
Х2
min
Слайд 5Экстремумы функции
Х0 - точка максимума (max) функции, если существует такая окрестность
точки х0 , что для всех х ≠ х0 из этой окрестности выполняется неравенство
f(x) ˂ f(x0 ).
f(x) ˂ f(x0 ).
Х0 - точка минимума (min)
функции, если существует такая окрестность точки х0 , что
для всех х ≠ х0 из этой окрестности выполняется неравенство
f(x) ˃ f(x0 ).
Слайд 6Рисунок 1
Рисунок 2
По заданным графикам функций y=f(x) укажите:
-критические точки;
-стационарные точки;
-экстремумы функции.
Слайд 7Алгоритм поиска точек экстремума функции:
1. Найти производную функции;
2.Приравнять производную к нулю
– найти стационарные точки;
3. Исследовать производную на «знак» - сделать вывод.
Слайд 9 На рисунке изображен график функции
, определенной на интервале . Найдите сумму точек экстремума функции.
3
-2+1+3+4+5+8+10=…
Слайд 10 На рисунке изображен график производной функции f(x), определенной на интервале (-9;8)
. Найдите точку экстремума функции на интервале (-3;3)
-3
3
+
-
