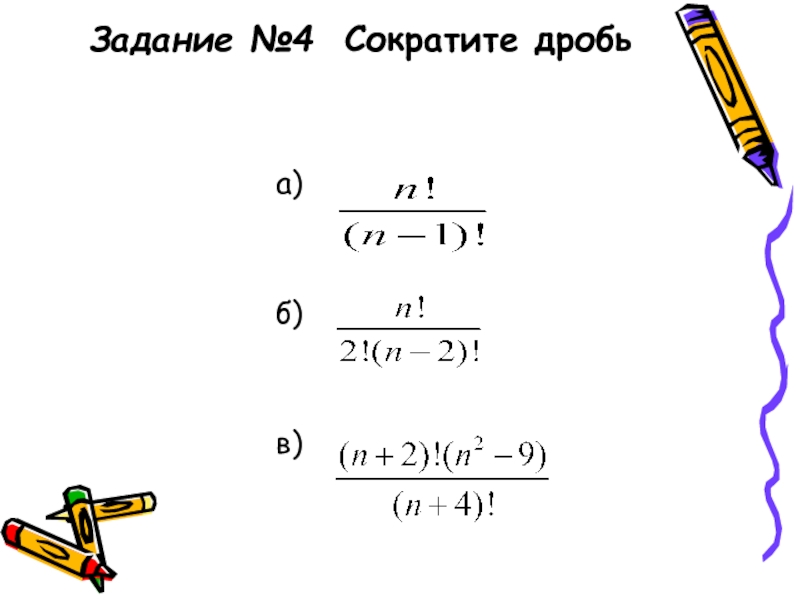- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к урокам математике по статистике для учащихся 11 класса по теме Перестановки.
Содержание
- 1. Презентация к урокам математике по статистике для учащихся 11 класса по теме Перестановки.
- 2. Урок №1. Тема урока : «Перестановки».
- 3. Основная цель: Ознакомить учащихся с понятиями перестановки и соответствующими формулами для подсчета их числа.
- 4. Знания и умения учащихся: знать основные правила
- 5. Часто из элементов
- 6. Сколько различных трехзначных чисел можно записать с
- 7. Сколько различных четырехзначных чисел можно записать с
- 8. Сколькими различными способами можно посадить за столом
- 9. Пусть дано произвольное множество из n элементов.
- 10. Мы установили, это множество из трёх цифр
- 11. Каждый способ упорядоче-ния множества каких либо элементов называется перестановкой этих элементов.
- 12. Теорема: Число перестановок из n элементов
- 13. Задача №1.Сколькими способами можно составить список из
- 14. Задача №2 Сколькими способами можно составить
- 15. Задание№3 Вычислите:
- 16. Задание №4 Сократите дробьа) б)в)
- 17. Задание №5 Решите уравнение:
- 18. Правило умножения:Если элемент А можно выбрать а
- 19. Задание №7. Сколькими способами можно расставить на
- 20. Задание №9.Выполните действия:Задание №10. Из цифр
- 21. Число перестановок из n элементов с повторениямиФОРМУЛА:
- 22. Задание на дом: Задача №1 .В пассажирском
- 23. Урок №2. Тема урока : «Перестановки».
- 24. Цель: закрепить изученный материал, применить полученные знания к решению практических задач.
- 25. Ход урока. Опрос. Устная работа.1. Делится
- 26. I I. Решение упражнений. Фронтальная работа:Вычислите
- 27. 4. Имеется девять различных книг, четыре из
- 28. III. Самостоятельная работа.Сколько существует вариантов рассадить
- 29. IV. Задание на дом:Что больше: 6! .5
Слайд 3Основная цель:
Ознакомить учащихся с понятиями перестановки и соответствующими формулами для
Слайд 4Знания и умения учащихся:
знать основные правила и методы решения комбинаторных
Слайд 5
Часто из элементов некоторого конечного множества приходится
В комбинаторике имеют дело только с конечными множествами. Этот раздел имеет большое значение в теории вероятности, теории, вычислительной техники, теории автоматов, в экономических расчётах.
Мы рассмотрим начальные сведения из комбинаторики.
Слайд 6Сколько различных трехзначных чисел можно записать с помощью трёх цифр: 3,5,7
Решение:
357,375,537,573,735,753.
Таких чисел будет 6.
Добавим к данным трем цифрам ещё одну, например 8. Тогда задача примет вид:
Слайд 7Сколько различных четырехзначных чисел можно записать с помощью цифр 3,5,7,8, не
Всего будет 24:
357 375 537 573 735 753
8357 8375 8537 8573 8735 8753
3857 3875 5837 5873 7835 7853
3587 3785 5387 5783 7385 7583
3578 3758 5378 5738 7358 7538
Слайд 8Сколькими различными способами можно посадить за столом четырёх человек, если к
По существу эта задача не отличается от предыдущей о четырех цифрах, поэтому и ответ будет тот же – 24.
Слайд 9
Пусть дано произвольное множество из n элементов. Упорядочить множество – значит
Слайд 10Мы установили, это множество из трёх цифр можно упорядочить шестью способами,
ВОПРОС:
Сколькими способами можно упорядочить множество из n элементов, где n- любое натуральное число?
Слайд 11
Каждый способ упорядоче-ния множества каких либо элементов называется перестановкой этих элементов.
Слайд 12
Теорема: Число перестановок из n элементов равно произведению n первых
Произведение n первых натуральных чисел обозначают n!
Например: 1! = 1; 2! = 1·2 = 2;
3! = 1·2·3 = 6; 4! = 1·2·3·4 = 24.
Слайд 13
Задача №1.
Сколькими способами можно составить список из 9 учеников?
Решение:
9! = 1·2·3...8·9 = 362880.
Слайд 14
Задача №2
Сколькими способами можно составить маршрут путешествия, проходящего через
Решение:
7! = 1·2...6·7 = 5040.
Слайд 17
Задание №5 Решите уравнение:
Задание №6
Сколько различных пятизначных чисел можно записать с помощью цифр 0,2,4,5,7, не повторяя их?
Слайд 18Правило умножения:
Если элемент А можно выбрать а способами и если после
Слайд 19Задание №7. Сколькими способами можно расставить на полке 12 книг, из которых
Задание №8
Сколько различных четных пятизначных чисел, все цифры, которых различны, можно записать с помощью цифр 1,2,3,4,5?
Слайд 20
Задание №9.
Выполните действия:
Задание №10. Из цифр 1,2,3,4,5,6,7 составляют всевозможные семизначные
Слайд 21Число перестановок из n элементов с повторениями
ФОРМУЛА:
Задание №11.
Сколько семизначных чисел
Слайд 22
Задание на дом:
Задача №1 .В пассажирском поезде 14 вагонов. Сколькими
Задача№2. Вычислить
Задача №3. Сократить дробь
Задача№4. В расписании на понедельник шесть уроков: алгебра, геометрия, биология, физкультура, химия, история. Сколькими способами можно составить расписание на этот день так, чтобы два урока математики стояли рядом?
Задача№5. Сколько среди всех перестановок букв слова «высота» таких, которые начинаются с буквы «а»,а оканчиваются буквой «т».
Слайд 24
Цель: закрепить изученный материал, применить полученные знания к решению
Слайд 25Ход урока.
Опрос. Устная работа.
1. Делится ли 11! на 64?
Делится ли
3. 15! Сколько нулей?
Слайд 26I I. Решение упражнений.
Фронтальная работа:
Вычислите 51! : 49!
Сократите дробь:
Упростите выражение:
Слайд 27
4. Имеется девять различных книг, четыре из которых – учебники. Сколькими
Слайд 28 III. Самостоятельная работа.
Сколько существует вариантов рассадить участников «Большой восьмерки» за
Вычислите:
Решите уравнение: (m +17)! = 420 (m + 15)!
Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа без повторения. Выясните, сколько среди этих пятизначных чисел таких, которые: а) начинаются цифрой 3; б) начинаются с 54?
У мамы 2 яблока, 3 груши и 4 апельсина. Каждый день в течение 9 дней подряд она выдает дочери по одному фрукту. Сколькими способами она сможет это сделать?
Слайд 29IV. Задание на дом:
Что больше: 6! .5 или 5! .6 ?
Выполните действие:
Сколькими способами можно записать в виде произведения простых множителей число 120?