- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к работе Проценты вокруг нас
Содержание
- 1. Презентация к работе Проценты вокруг нас
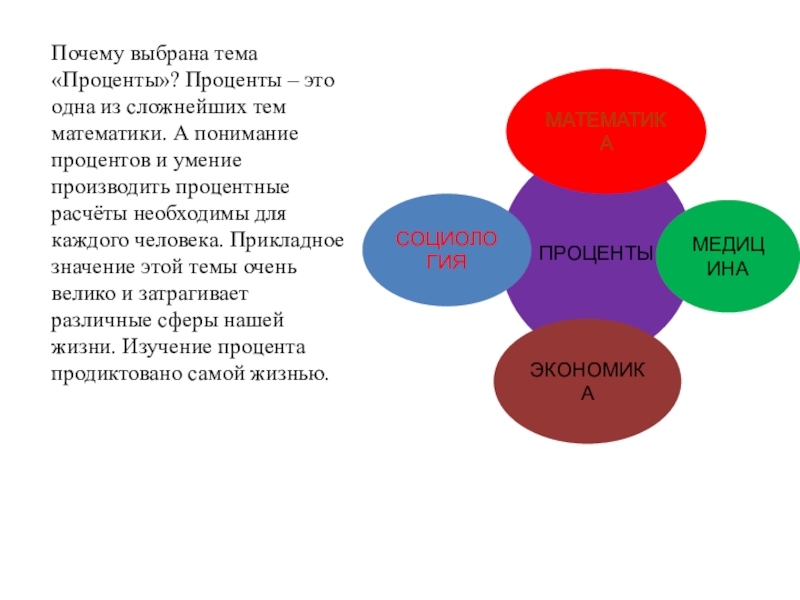
- 2. Почему выбрана тема «Проценты»? Проценты – это
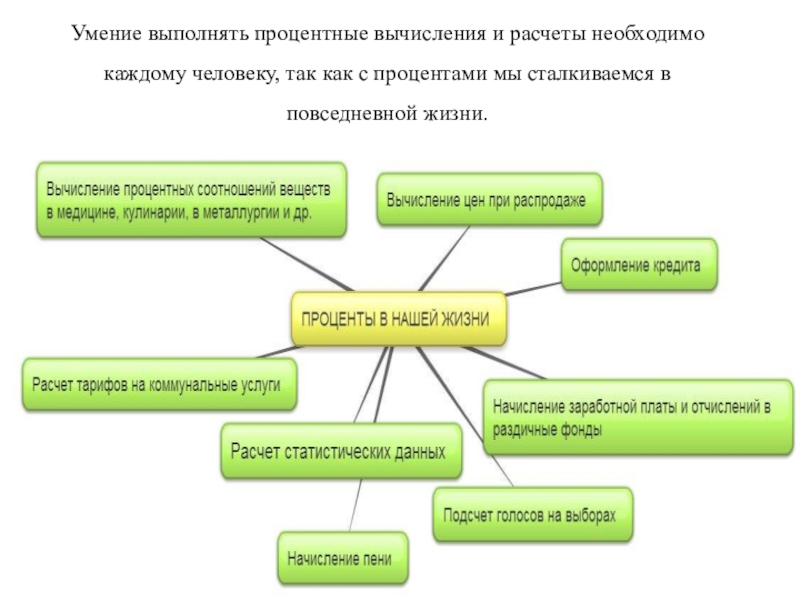
- 3. Умение выполнять процентные вычисления и расчеты необходимо
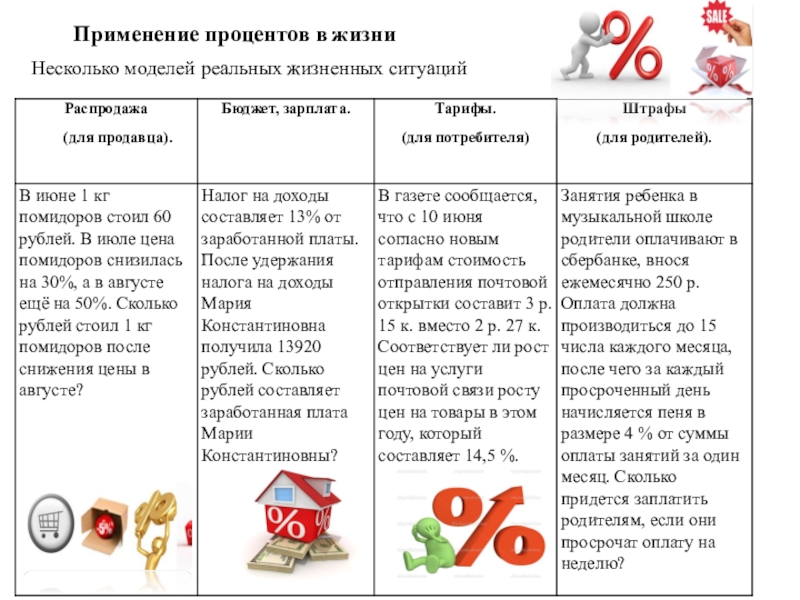
- 4. РаспродажаБюджет..ТарифыШтрафы
- 5. Цель исследовательской работы :Расширение знаний о применении
- 6. Слово «процент» происходит от латинского слова procentum,что
- 7. В средние века в Европе в связи
- 8. Впервые опубликовал таблицы для расчета процентов в
- 9. Знак процента появился в результате опечатки: наборщик
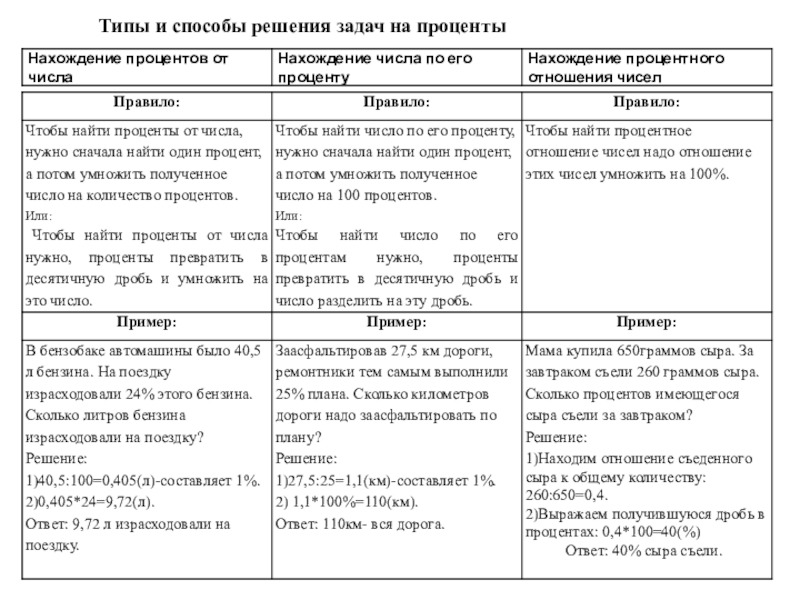
- 10. Типы и способы решения задач на проценты
- 11. Решение задач на проценты разными способамиЗадача 1.За
- 12. Задача 2Свежие грибы по массе содержат 90%
- 13. Сложные проценты - это проценты, полученные на
- 14. Пример:Представим, что вы положили 10 000 руб.
- 15. Рассмотрим два примера:Пример1. Предположим что банком принят
- 16. Рассмотрим задачу:По пенсионному вкладу банк выплачивает 12%
- 17. Эту же задачу решим по формуле банковских
- 18. Задание 11 № 99569.(ЕГЭ 2016) Цена холодильника в магазине
- 19. Применение процентов в жизниНесколько моделей реальных жизненных ситуаций
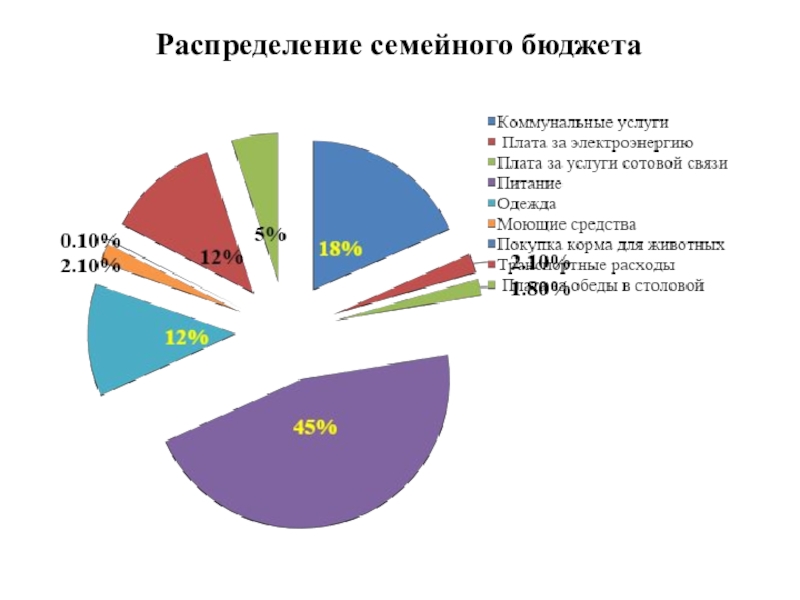
- 20. Распределение семейного бюджета
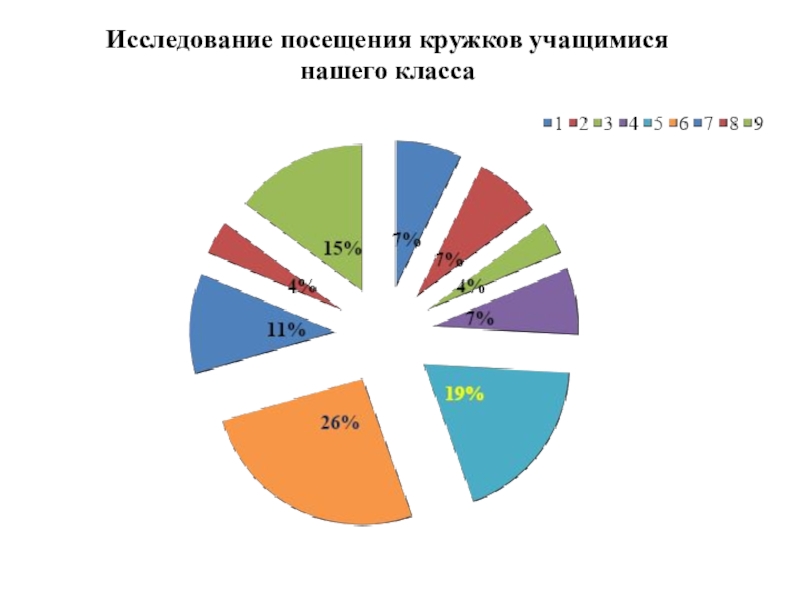
- 21. Исследование посещения кружков учащимися нашего класса
- 22. Провели анализ умения решать задачи на %
- 23. Количество верно выполненных задач (в процентах). %
- 24. Слайд 24
- 25. Проценты окружают нас повсюду: с экрана телевизора,
- 26. Слайд 26
- 27. Спасибо за внимание
- 28. Слайд 28
- 29. Слайд 29
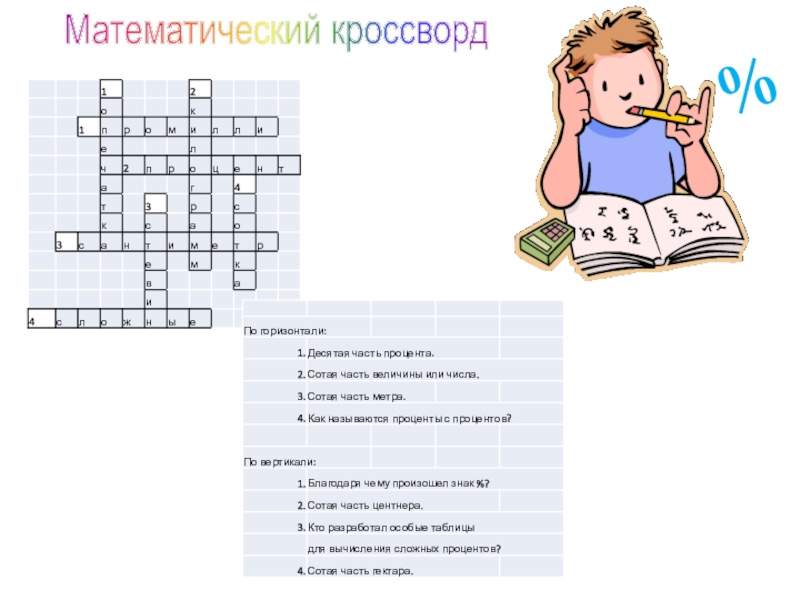
- 30. Математический кроссворд%
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Задача (ЕГЭ)Вследствие инфляции цены выросли на 150%.
Слайд 1Проценты
вокруг нас
Работу выполнили ученики 7 «В» класса,
МОУ «Гимназия №34»
Соколов
Руководитель работы: учитель математики
МОУ «Гимназия №34»
Хренникова Наталья Игорьевна
Слайд 2Почему выбрана тема «Проценты»? Проценты – это одна из сложнейших тем
ПРОЦЕНТЫ
СОЦИОЛОГИЯ
ЭКОНОМИКА
МЕДИЦИНА
МАТЕМАТИКА
Слайд 3Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как
повседневной жизни.
Слайд 5Цель исследовательской работы :
Расширение знаний о применении процентных вычислений в задачах
Задачи:
-Познакомиться с историей возникновения процентов;
-Решать задачи на проценты разными способами;
-Сделать подборку задач из ГИА – 9 кл., ЕГЭ -11кл., решаемые по формуле сложных процентов;
-Исследовать бюджет семьи и посещаемость кружков учащихся моего класса;
-Научиться составлять различные диаграммы и таблицы;
-Поработать в текстовом редакторе;
-Поработать с ресурсами Internet;
-Получить опыт публичного выступления.
Слайд 6Слово «процент» происходит от латинского слова procentum,что означает «за сотню» или
Были известны проценты и в Индии. Индийские математики вычисляли проценты, применив так называемое тройное правило, т. е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов.
Слайд 7В средние века в Европе в связи с широким развитием торговли
Слайд 8Впервые опубликовал таблицы для расчета процентов в 1584 году Симон Стевин
Долгое время под процентами понимались исключительно прибыль и убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Нынче процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу).
Слайд 9Знак процента появился в результате опечатки: наборщик переставил цифры в числе
Существует версия, что знак %
происходит от Латинского pro cento (сто),
которое в процентных расчетах часто
сокращенно писалось cto.
Отсюда путем дальнейшего сокращения
в скорописи буква t превратилась
в наклонную черту (/), возник
современный знак процента.
Слайд 11Решение задач на проценты разными способами
Задача 1.
За первый год предприятие увеличило
Эту задачу можно решить двумя способами:
1) используя пропорцию
2) по действиям
1 способ: Узнаю на сколько увеличился выпуск продукции за первый год.
Пусть: х – начальный выпуск, у – после увеличения на 8%
х – 100% у = х*8 = 1,08х
у – 108% 100
Теперь, узнаю на сколько увеличился выпуск продукции за второй год.
Пусть: 1.08х – теперь уже начальный выпуск, z – после увеличения на 25%, тогда
1,08х – 100% z= 1,08х*125 = 1,35х
z – 125% 100
Значит выпуск увеличился на 0,35 или на 35%
2 способ:
1) 1,00+0,08=1,08 (узнали выпуск продукции после первого увеличения)
2)1,00+0,25=1,25 (узнали выпуск продукции после второго увеличения)
3)1,08*1,25=1,35 (это выпуск продукции после двух увеличений)
4)1,35-1,00=0,35 (увеличения выпуска продукции после двух прибавок)
ОТВЕТ: выпуск продукции по сравнению с первоначальной вырос на 35%.
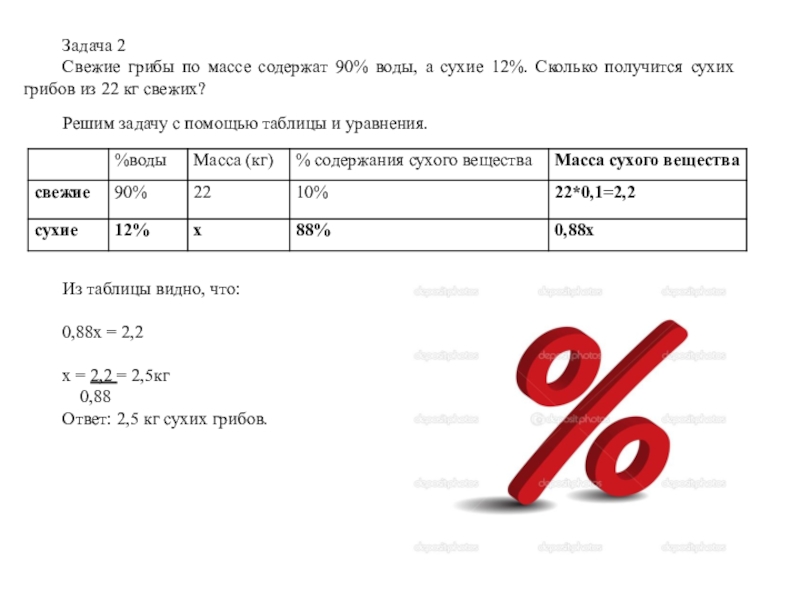
Слайд 12Задача 2
Свежие грибы по массе содержат 90% воды, а сухие 12%.
Решим задачу с помощью таблицы и уравнения.
Из таблицы видно, что:
0,88х = 2,2
х = 2,2 = 2,5кг
0,88
Ответ: 2,5 кг сухих грибов.
Слайд 13Сложные проценты - это проценты, полученные на начисленные проценты.
Формула сложного процента
х (1+ 0,01а)n - периодическое увеличение некоторой величины на одно и то же число процентов.
х(1+ 0,01а)n,
где х - начальный вклад, сумма.
а – процент(ы) годовых
n- время размещения вклада в банке
Но, мы можем и уменьшать цену, поэтому эту формулу можно записать и по- другому: х(1- 0,01а)n - периодическое уменьшение некоторой величины на одно и то же число процентов.
Задачи на сложные проценты.
Сложным процентом называется сумма дохода, которая образуется в результате вложения денег при условии, что сумма начисленного простого процента не выплачивается в конце каждого периода, а присоединяется к сумме основного вклада и в следующем платежном периоде сама приносит доход.
Слайд 14Пример:
Представим, что вы положили 10 000 руб. в банк под 10
Через год на вашем банковском счету будет лежать
сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль - 1000 рублей.
Вы решили оставить 11 000 руб. на второй год в банке под те же 10%.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.
Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10 000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.
Этот эффект и получил название сложный процент. Когда вся прибыль прибавляется к основной сумме и в дальнейшем уже сама производит новую прибыль.
Слайд 15Рассмотрим два примера:
Пример1. Предположим что банком принят депозит в сумме 60
Sp = 60 000 * 10,2 * 90 : 365 : 100 = 1509,041
S = 60 000 + 60 000 * 10,2 * 30 : 365 : 100 = 61509,041
Пример 2. Принят вклад в сумме 60 000 рублей сроком на 90 дней по ставке 10,2 процентов годовых с начислением процентов каждые 30 дней.
S = 60 000 * (1 + 10,2 * 30 : 365 :100)3 = 61521,708
Sp = 60 000 * [(1 + 10,2 * 30 : 365 : 100)3 -1] = 1521,708
А теперь давайте сделаем простое сравнение результатов расчета процентов, при применении двух различных формул. В обоих примерах за основу были взяты одни и те же данные, т.е. сбережения в сумме 60000,00 рублей, размещены во вклад со сроком 90 дней.
При расчете процентов по формуле простых процентов доход составил 61509,041 руб. При расчете процентов по формуле сложных
процентов, доход составил 61521,708 руб. Капитализация процентов составила 12,667 руб. (61521,708 -61509,041).
Вывод: больший доход получается с капитализацией процентов,
в этом случае при вычислении применяется формула сложных процентов.
Слайд 16Рассмотрим задачу:
По пенсионному вкладу банк выплачивает 12% годовых. По истечению каждого
Эту задачу можно решить двумя способами:
1)по действиям
2)по формуле сложных процентов
Решение:
1)узнаем доход за первый год
80000*0.12=9600руб.
2)найдем сумму на счете после первого года
80000+ 9600= 89600руб.
3)определим доход за второй год
89600* 0,12= 10752 руб.
4)узнаем конечную сумму на счете
10752 + 89600= 100352руб.
5)найдем доход после двух лет
100352- 80000= 20352 руб.
Слайд 17Эту же задачу решим по формуле банковских процентов: х(1 + 0,01а)n
Пусть:
а – 12% годовых
n – 2 года, получим:
80000(1+ 0,12)2 = 80000 * 1,122 = 100 352 руб.
Этим узнали конечную сумму на счете после двух лет. Теперь надо узнать какой доход был получен. Для этого из конечной суммы вычтем начальный вклад.
100352 – 80000 = 20 352руб.
ОТВЕТ: по истечении срока был получен доход в размере 29 352 руб.
Вывод: решив задачу двумя способами видим,
что проще и быстрее решить задачу
по формуле сложных
процентов, а не по действиям.
Слайд 18 Задание 11 № 99569.(ЕГЭ 2016) Цена холодильника в магазине ежегодно уменьшается на одно
Решение.
Пусть цена холодильника ежегодно снижалась на p
процентов в год. Тогда за два года она снизилась
на , откуда имеем:
Ответ: 11.
Слайд 22Провели анализ умения решать задачи на %
в различных классах
1 вариант.
1.В
2.Выразите в процентах 2/5 всех жителей города.
3.Найдите 15% от 30000руб.
4.Сколько будет, если 30000руб. Увеличить на 15%?
5.Сколько процентов составляют 500руб. от 200руб.?
6.40% от некоторой суммы составляют 100руб. Какова эта сумма?
2 вариант.
1.Вскопали 45% поля. Сколько процентов поля осталось вскопать?
2.Выразите в процентах ¾ всех жителей города.
3.Найдите 35% от 10000руб.
4.Сколько будет, если 10000руб. уменьшить на 35%?
5.Сколько процентов составляют 600руб. от 400руб.?
6.30% от некоторой суммы составляют 150руб. Какова эта сумма?
Слайд 25Проценты окружают нас повсюду: с экрана телевизора, по радиоприемникам, рекламных щитов,
чтобы увеличить (уменьшить) величину на 50 %, достаточно прибавить (вычесть)ее половину;
чтобы найти 20 % величины, надо найти ее пятую часть;
чтобы найти 25 % величины, надо найти ее четверть;
что 40 % некоторой величины в 4 раза больше, чем ее 10 %;
что треть величины - это примерно 33 %,
увеличение (уменьшение) на 100% означает увеличение (уменьшение) в два раза.
-Если число А больше числа В на какое-то число процентов, то число В меньше числа А совсем на другое число процентов
Слайд 26
В ходе проделанной работы мы узнали, что сложные проценты – это проценты, полученные на начисленные проценты.
Формула сложного процента - это формула, по которой рассчитывается итоговая сумма с учётом начисления процентов. Подробнее изучила правила нахождения процентов. Сделала подборку и решила задачи из ЕГЭ – 11 классов и ГИА – 9 классов. Исследовали бюджет семьи и посещаемость кружков, учащимися нашего класса. Результаты занесены в таблицы и диаграммы. Освоили навыки работы в текстовом редакторе, с программой построения диаграмм и поработали с ресурсами интернета.
Выполненный проект «Проценты вокруг нас», на наш взгляд, демонстрирует применение математического аппарата к решению повседневных бытовых проблем каждого из нас, вопросов рыночной экономики и задач технологии производства; ориентирует на обучение по естественно - научному и социально- экономическому профилю.
Слайд 35Задача (ЕГЭ)
Вследствие инфляции цены выросли на 150%. Дума потребовала от правительства
Решение:
Решим эту задачу с помощью пропорций.
Пусть: х – первоначальная цена
у – цена после повышения цен на 150%
х– 100% у = 250х; у = 2,5х (новая цена)
у– 250% 100
2,5х – 100% 100*х = 40%
х- ?% 2,5х
40% - составила первоначальная цена от инфляции,
поэтому цены должны быть уменьшены на 60%
100% - 40% = 60%
ОТВЕТ: цены должны быть уменьшены на 60%.