- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к первому уроку по теме Производная
Содержание
- 1. Презентация к первому уроку по теме Производная
- 2. ПриращениеЧасто нас интересует не значение какой-либо величины,
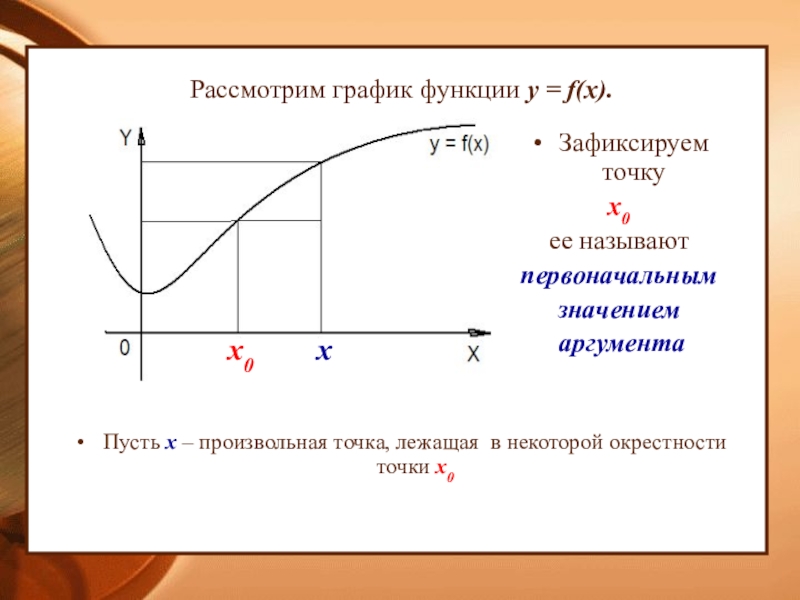
- 3. Рассмотрим график функции у = f(x). Пусть
- 4. Обозначаются Δх и Δf соответственнох - х0 приращение аргументах0 х f(x)f(х0)ΔхΔff(x) - f(х0) приращение функции.
- 5. Диктант Вариант IВариант II
- 6. 1. Найдите ∆x, если Вариант Iх0 =
- 7. 2. Найдите ∆f, если Вариант If (х0
- 8. 3. Найдите приращение функции: Вариант If(х) =
- 9. Ответы: Вариант I1. ∆х = - 0,22.
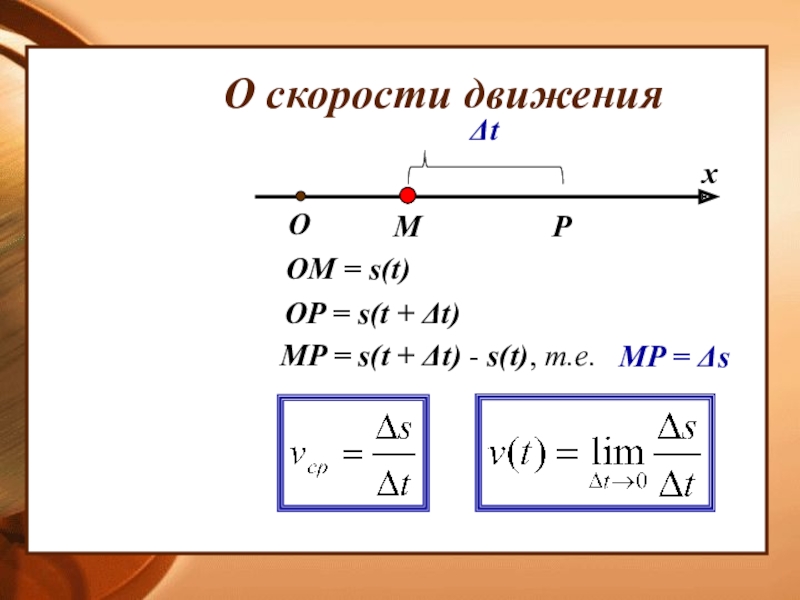
- 10. Задачи, приводящие к понятию производнойО скорости движенияО касательной к графику функции
- 11. О скорости движенияOMPxOM = s(t)OP = s(t
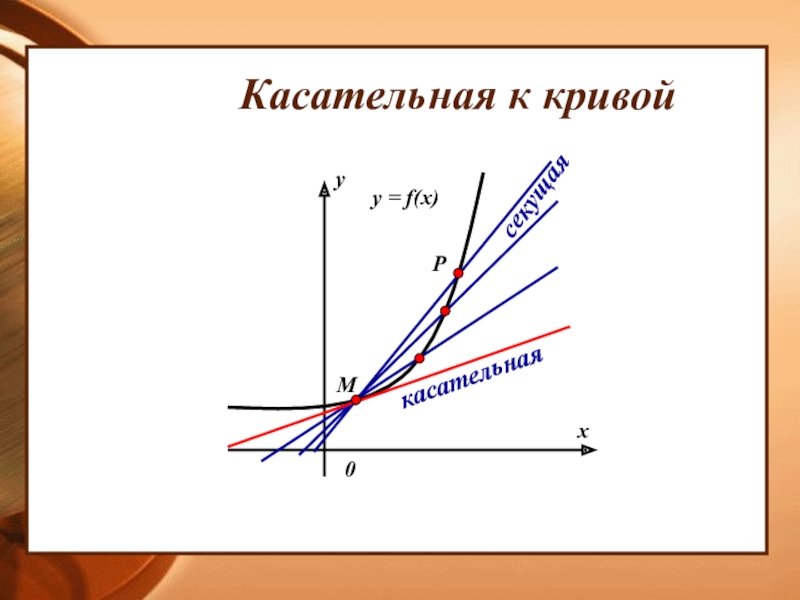
- 12. Касательная к кривойМРкасательнаясекущая
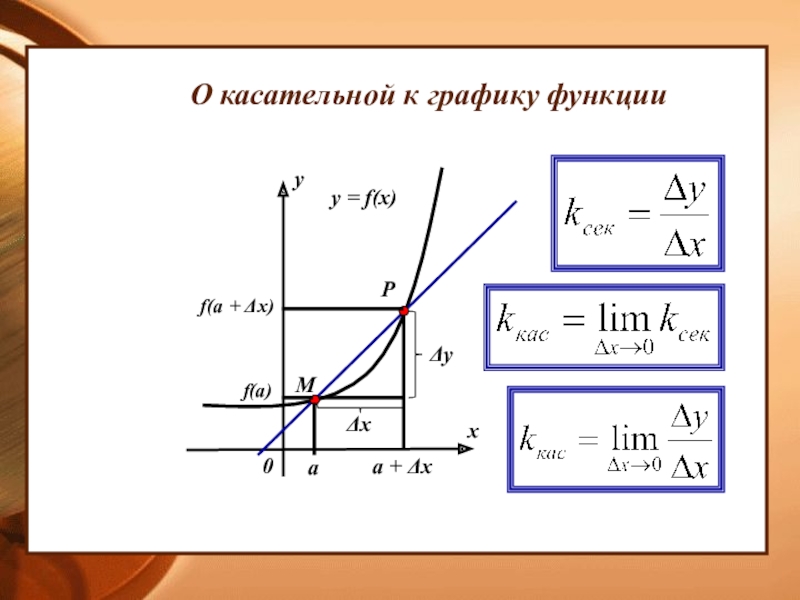
- 13. О касательной к графику функции xy0y = f(x)МРаа + Δхf(а)f(а + Δх)ΔхΔу
- 14. Сравните математические модели:
- 15. Определение производнойдифференцирование
- 16. Алгоритм отыскания производнойЗафиксировать значение х, найти f(x)Дать
- 17. Задачи, приводящие к понятию производнойО скорости движенияО касательной к графику функцииФизический смысл производнойГеометрический смысл производной
ПриращениеЧасто нас интересует не значение какой-либо величины, а ее изменение.Например - сила упругости пружины пропорциональна удлинению пружины - работа есть изменение энергии и т.д.
Слайд 2Приращение
Часто нас интересует не значение какой-либо величины, а ее изменение.
Например
- сила
упругости пружины пропорциональна удлинению пружины
- работа есть изменение энергии и т.д.
- работа есть изменение энергии и т.д.
Слайд 3Рассмотрим график функции у = f(x).
Пусть х – произвольная точка, лежащая
в некоторой окрестности точки х0
Зафиксируем точку
х0
ее называют
первоначальным
значением
аргумента
х0
х
Слайд 4Обозначаются Δх и Δf соответственно
х - х0
приращение
аргумента
х0
х
f(x)
f(х0)
Δх
Δf
f(x) - f(х0)
приращение
функции.
Слайд 83. Найдите приращение функции:
Вариант I
f(х) = 3х – 1,
х0
= 1, х = 1,2
Вариант II
f(х) = 2х + 3
х0 = 1, х = 1,2
Слайд 9Ответы:
Вариант I
1. ∆х = - 0,2
2. ∆f = - 3,4
3.
∆f = 0,6
Вариант II
1. ∆х = - 0,3
2. ∆f = 5,6
3. ∆f = 0,4
Слайд 16Алгоритм отыскания производной
Зафиксировать значение х, найти f(x)
Дать аргументу х приращение Δх,
найти f(x+Δх)
Найти приращение функции
Составить отношение
Вычислить предел
Этот предел и есть
Слайд 17Задачи, приводящие к понятию производной
О скорости движения
О касательной к графику функции
Физический
смысл производной
Геометрический смысл производной