№19», г.Абакан, 2014г.,
учитель математики Быковская И.С.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад (к конспекту урока) Графическое решение квадратных уравнений. 8 класс
Содержание
- 1. Презентация (к конспекту урока) Графическое решение квадратных уравнений. 8 класс
- 2. Графическое решение квадратных уравнений «Нельзя изучать математику, глядя, как это делает сосед».А.Нивен
- 3. Закрепить и систематизировать полученные знания
- 4. Обучающие: 1.Обзор графических способов решения квадратных уравнений:2.Построение
- 5. компьютервидеопроекторинтерактивная доскапрезентация раздаточный материал: шаблон параболы памятка ( алгоритмы 1-3)чертежные принадлежностиОборудование:
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
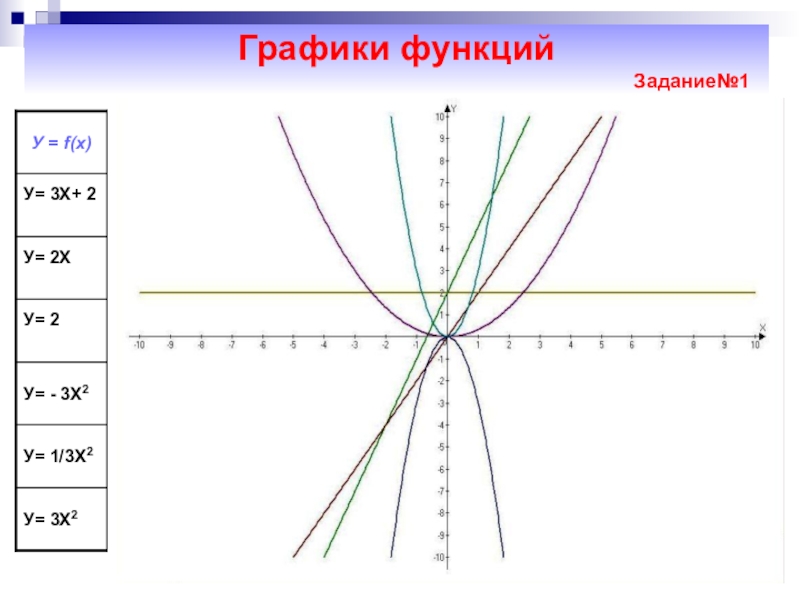
- 9. Графики функций
- 10. Алгоритм построения параболы
- 11. 1. Как из графика функции у =
- 12. Квадратным уравнением называется уравнение вида аx2 +
- 13. Найти абсциссы точек пересечения параболы у= аx2
- 14. Число корней уравнения аx2 + bx +c=0
- 15. СПОСОБЫ РЕШЕНИЯ
- 16. СПОСОБ РЕШЕНИЯ №1
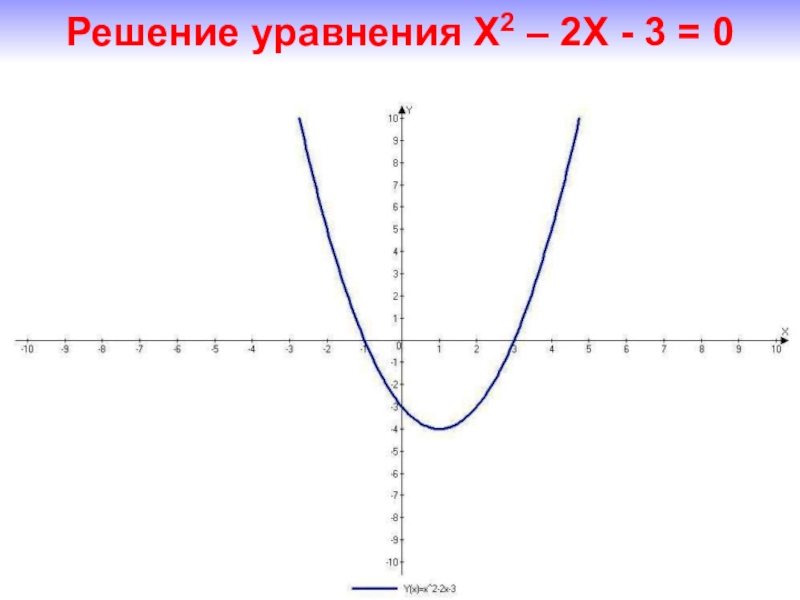
- 17. Решение уравнения Х2 – 2Х - 3 = 0
- 18. СПОСОБЫ РЕШЕНИЯ №2-4
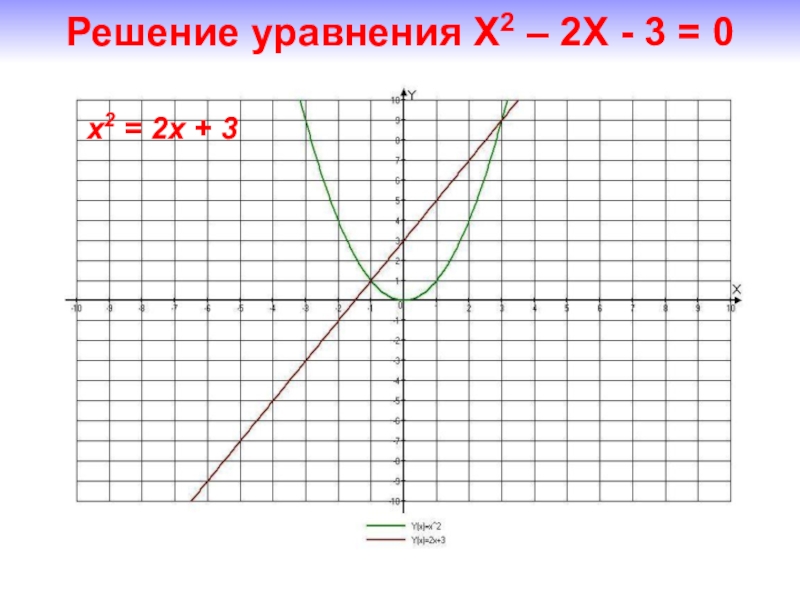
- 19. Решение уравнения Х2 – 2Х - 3 = 0x2 = 2x + 3
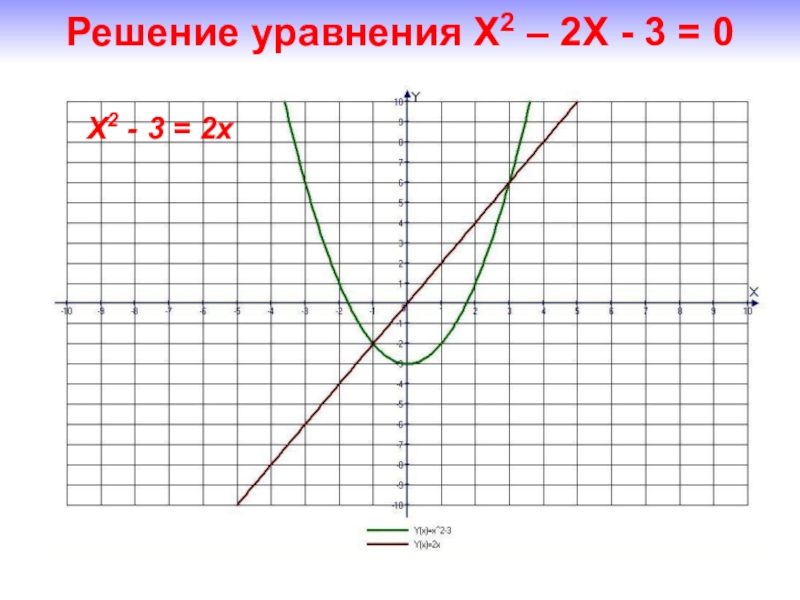
- 20. X2 - 3 = 2xРешение уравнения Х2 – 2Х - 3 = 0
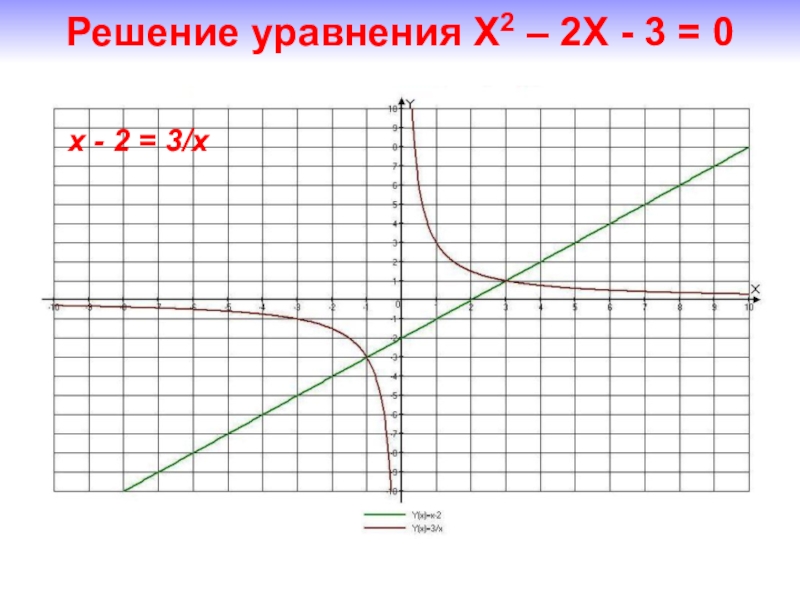
- 21. x - 2 = 3/x Решение уравнения Х2 – 2Х - 3 = 0
- 22. СПОСОБ РЕШЕНИЯ №5
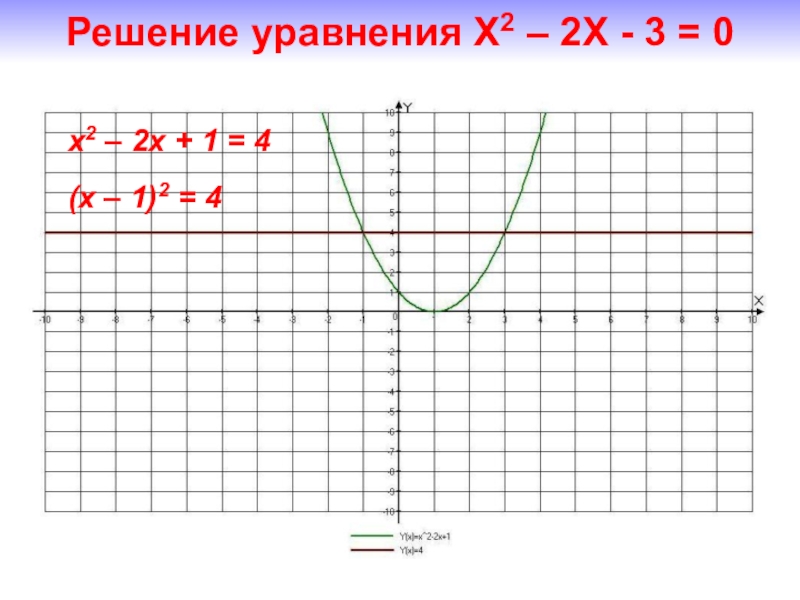
- 23. x2 – 2x + 1 = 4
- 24. Число корней уравнения аx2 + bx +c=0Решение уравнения Х2 – 2Х - 3 = 0
- 25. Число корней уравнения аx2 + bx +c=0Решение
- 26. Защита работы, выполненной с помощью компьютера1. Достоинства
- 27. Графический способ решения квадратных уравнений1.Достоинства способа: Возможность
- 28. Домашняя работа 1.Практическая работа « Графическое решение
- 29. Итог урокаОбобщили способы графического решения квадратичных уравнений.Сравнивали
- 30. Я есть парабола!Я есть парабола! Взгляните!Как я
- 31. УСПЕХОВ ВАМ, РЕБЯТА!
Графическое решение квадратных уравнений «Нельзя изучать математику, глядя, как это делает сосед».А.Нивен
Слайд 2Графическое
решение квадратных уравнений
«Нельзя изучать математику, глядя,
как это делает
сосед».
А.Нивен
А.Нивен
Слайд 3
Закрепить и систематизировать полученные знания по решению квадратных уравнений
при графическом решении квадратных уравнений разными способами
Цель урока:
Слайд 4Обучающие:
1.Обзор графических способов решения квадратных уравнений:
2.Построение графиков квадратичной функции функций
с помощью компьютерного моделирования и алгоритмов 1-3
3.Систематизация знаний по способам решения квадратных уравнений
Развивающие:
Развитие навыков геометрической иллюстрации математической модели – функции и навыков чтения геометрической модели – графика функции.
Умение выполнять простейшие операции на интерактивной доске;
Построение графиков функций с помощью компьютера.
Воспитывающие:
Совершенствование умений публично выступать, выражать свое собственное мнение ;
Совершенствование приема групповой работы
3.Систематизация знаний по способам решения квадратных уравнений
Развивающие:
Развитие навыков геометрической иллюстрации математической модели – функции и навыков чтения геометрической модели – графика функции.
Умение выполнять простейшие операции на интерактивной доске;
Построение графиков функций с помощью компьютера.
Воспитывающие:
Совершенствование умений публично выступать, выражать свое собственное мнение ;
Совершенствование приема групповой работы
Задачи урока:
Слайд 5компьютер
видеопроектор
интерактивная доска
презентация
раздаточный материал:
шаблон параболы
памятка ( алгоритмы 1-3)
чертежные принадлежности
Оборудование:
Слайд 11
1. Как из графика функции у = ах² получить график функции
у = ах² + в? Назвать у = ах²
у = -0,5х² - 3 и у = -0,5 х² + 3;
2. Как из графика функции у = ах² получить график функции
у =а(х –m)²? Назвать у = ах²
у = 2(х + 2)² и у = 2(х - 2)² .
3. Назовите координаты начала новой системы координат:
у = (х + 2)² - 4 и у = (х - 2)² + 4
4. Назовите уравнение оси симметрии параболы следующих квадратичных функций:
y = x2 + 4x -5 и у = -0,5 х² +2х- 3,
у = -0,5х² - 3 и у = -0,5 х² + 3;
2. Как из графика функции у = ах² получить график функции
у =а(х –m)²? Назвать у = ах²
у = 2(х + 2)² и у = 2(х - 2)² .
3. Назовите координаты начала новой системы координат:
у = (х + 2)² - 4 и у = (х - 2)² + 4
4. Назовите уравнение оси симметрии параболы следующих квадратичных функций:
y = x2 + 4x -5 и у = -0,5 х² +2х- 3,
Задание №2
Слайд 12Квадратным уравнением называется уравнение вида
аx2 + bx +c=0, где а,
b,с – коэффициенты
а- старший член
с – свободный член
а- старший член
с – свободный член
Квадратное уравнение
Слайд 13
Найти абсциссы точек пересечения параболы у= аx2 + bx +c с
осью х
или
Построить графики функций в одной системе координат
Найти абсциссу точки пересечения графиков функций - корень уравнения.
или
Построить графики функций в одной системе координат
Найти абсциссу точки пересечения графиков функций - корень уравнения.
Решить уравнение графически
Слайд 25Число корней уравнения аx2 + bx +c=0
Решение уравнения Х2 – 2Х
- 3 = 0
Решение уравнения Х2 – 2Х - 3 = 0
Слайд 26Защита работы, выполненной с помощью компьютера
1. Достоинства способа:
Наглядность, быстрота работы, точность построения, простота реализации, возможность автоматизации проверки результата; создается график не только на бумаге, но и в электронном виде.
2. Недостатки способа:
Не совершенствуются вычислительные навыки, отсутствует связь с теорией, наличие технических средств и программного обеспечения.
2. Недостатки способа:
Не совершенствуются вычислительные навыки, отсутствует связь с теорией, наличие технических средств и программного обеспечения.
Слайд 27Графический способ решения квадратных уравнений
1.Достоинства способа:
Возможность применения компьютерного моделирования
наглядность ,
красота
2. Недостатки способа:
Длительность работы по времени, ограниченность тетрадного листа, не всегда координаты точек пересечения графиков функции «хорошие»
2. Недостатки способа:
Длительность работы по времени, ограниченность тетрадного листа, не всегда координаты точек пересечения графиков функции «хорошие»
Слайд 28Домашняя работа
1.Практическая работа
« Графическое решение квадратного уравнения
несколькими
способами»
№509 (в)
«5» - 5 способов
«4» - 4 способа
«3» - 3 способа
2.Составить кроссворд по теме « Квадратное уравнение»
3.Пополнение видеоряда
№509 (в)
«5» - 5 способов
«4» - 4 способа
«3» - 3 способа
2.Составить кроссворд по теме « Квадратное уравнение»
3.Пополнение видеоряда
Слайд 29Итог урока
Обобщили способы графического решения квадратичных уравнений.
Сравнивали способы графического решения квадратичных
уравнений с аналитическим.
Использовали при графическом способе решения квадратичных уравнений интерактивную доску и компьютер.
Использовали при графическом способе решения квадратичных уравнений интерактивную доску и компьютер.
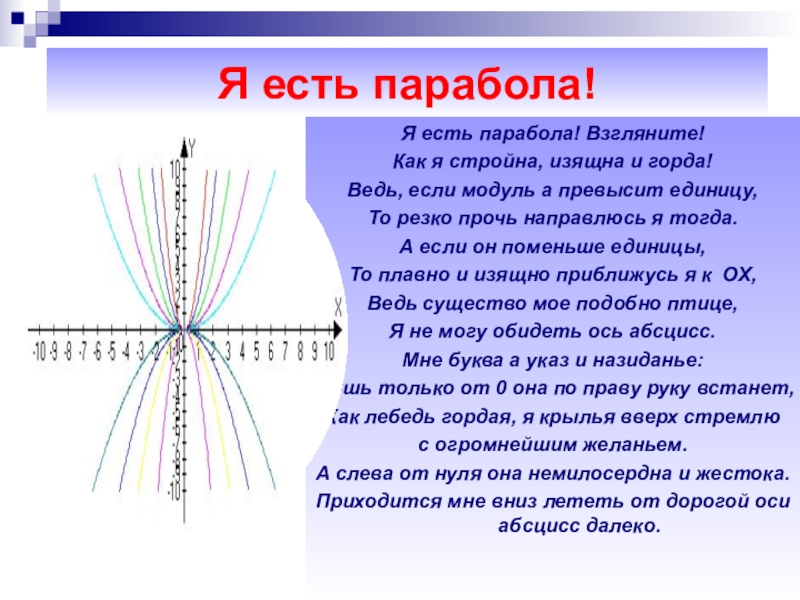
Слайд 30Я есть парабола!
Я есть парабола! Взгляните!
Как я стройна, изящна и горда!
Ведь,
если модуль а превысит единицу,
То резко прочь направлюсь я тогда.
А если он поменьше единицы,
То плавно и изящно приближусь я к ОХ,
Ведь существо мое подобно птице,
Я не могу обидеть ось абсцисс.
Мне буква а указ и назиданье:
Лишь только от 0 она по праву руку встанет,
Как лебедь гордая, я крылья вверх стремлю
с огромнейшим желаньем.
А слева от нуля она немилосердна и жестока.
Приходится мне вниз лететь от дорогой оси абсцисс далеко.
То резко прочь направлюсь я тогда.
А если он поменьше единицы,
То плавно и изящно приближусь я к ОХ,
Ведь существо мое подобно птице,
Я не могу обидеть ось абсцисс.
Мне буква а указ и назиданье:
Лишь только от 0 она по праву руку встанет,
Как лебедь гордая, я крылья вверх стремлю
с огромнейшим желаньем.
А слева от нуля она немилосердна и жестока.
Приходится мне вниз лететь от дорогой оси абсцисс далеко.