- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад и конспект урока Координатный метод решения задач №16 второй части ЕГЭ
Содержание
- 1. Презентация и конспект урока Координатный метод решения задач №16 второй части ЕГЭ
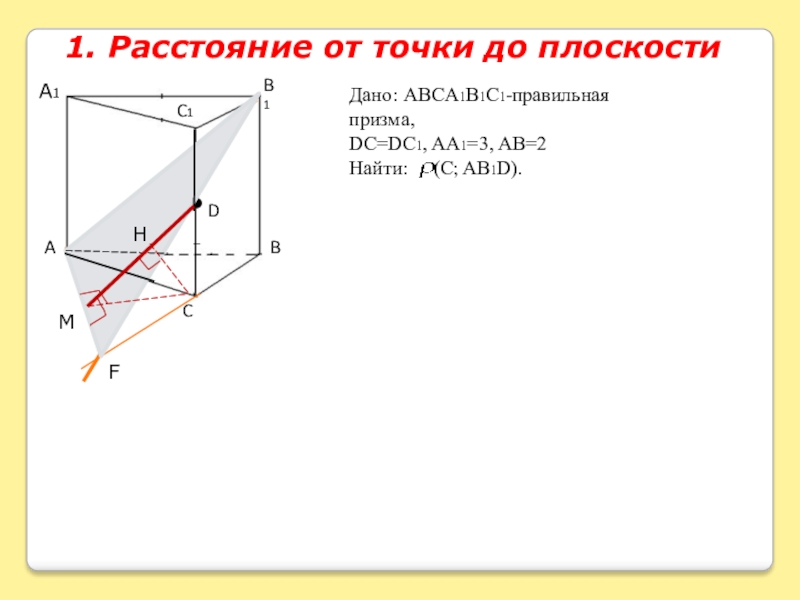
- 2. A1ABB1DCC1FHM1. Расстояние от точки до плоскостиC1
- 3. A1ABB1ZDCXYOC1Составим уравнение плоскости AB1D. Так как точки
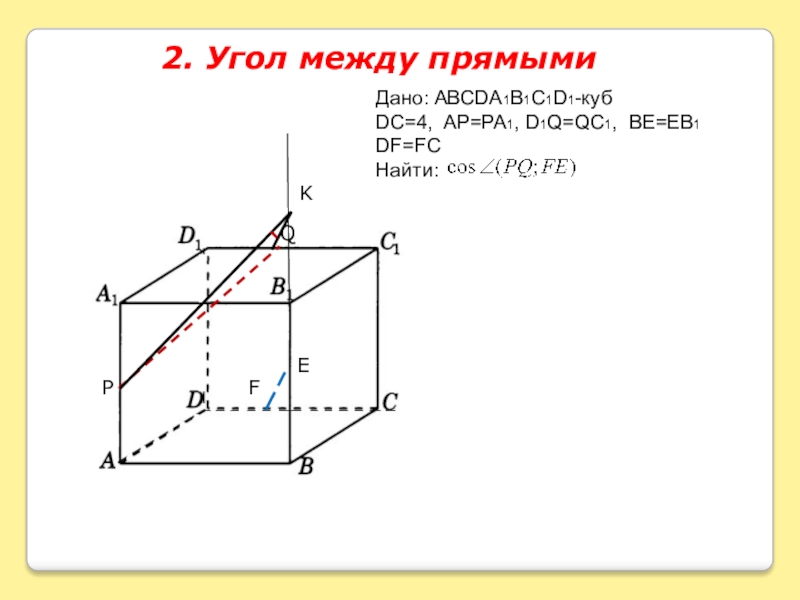
- 4. 2. Угол между прямымиДано: ABCDA1B1C1D1-кубDC=4, AP=PA1, D1Q=QC1, BE=EB1DF=FCНайти: QPEFK
- 5. 2. Угол между прямыми Введем прямоугольную систему
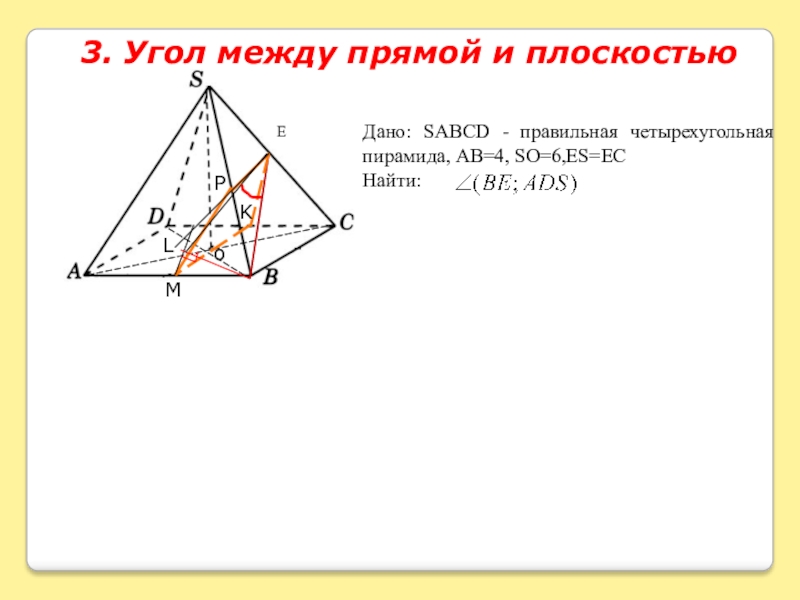
- 6. 3. Угол между прямой и плоскостьюEoMPKL
- 7. Угол между прямой и плоскостьюExyzo- уравнение плоскости АSD. Ax+By+Cz+D=0 Значит координаты нормали Ответ: .
- 8. 4. Угол между плоскостямиMPED
- 9. Угол между плоскостями, . В плоскости ВА1D1C
Слайд 3A1
A
B
B1
Z
D
C
X
Y
O
C1
Составим уравнение плоскости AB1D. Так как точки A, B1 ИD
принадлежат
в уравнение плоскости. Получим:
Подставим коэффициенты в уравнение плоскости: dy-
dz+d=0, 3y-2z-3=0 – уравнение плоскости АB1D
Ответ:
.
Расстояние от точки C до плоскости AB1D находим по формуле
Расстояние от точки до плоскости
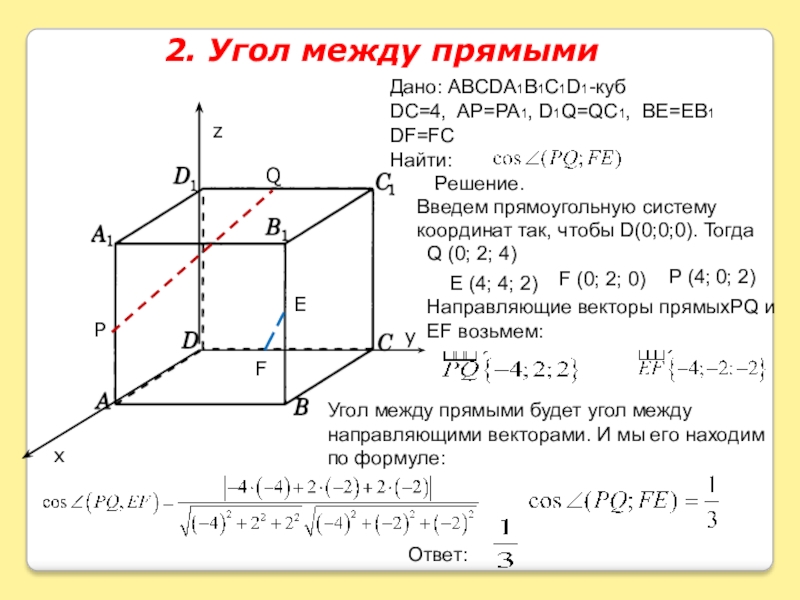
Слайд 52. Угол между прямыми
Введем прямоугольную систему
координат так, чтобы D(0;0;0).
Направляющие векторы прямыхPQ и EF возьмем:
Р (4; 0; 2)
Q (0; 2; 4)
E (4; 4; 2)
F (0; 2; 0)
Дано: ABCDA1B1C1D1-куб
DC=4, AP=PA1, D1Q=QC1, BE=EB1
DF=FC
Найти:
Решение.
Угол между прямыми будет угол между направляющими векторами. И мы его находим по формуле:
Ответ:
.
x
y
z
F
E
P
Q
Слайд 7Угол между прямой и плоскостью
E
x
y
z
o
- уравнение плоскости АSD.
Ax+By+Cz+D=0
Значит координаты нормали
Ответ:
.
Слайд 9Угол между плоскостями
,
. В плоскости ВА1D1C лучше взять ВА1C, где
– уравнение плоскости ВА1C. Координаты нормали
Координаты нормали плоскости АА1Е1
.
Ответ:
.