- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для подготовки к ЕГЭ по математике
Содержание
- 1. Презентация для подготовки к ЕГЭ по математике
- 2. Формулы которые необходимо знать! Формула объёма шара:Формула площади поверхности шара:Формула объёма цилиндра:Формула площади поверхности цилиндра:
- 3. Особенности представленных задач1. Если шар вписан в
- 4. Необходимо найти радиус шара.У шара и у
- 5. Цилиндр описан около шара. Объем шара равен
- 6. Шар вписан в цилиндр. Площадь поверхности шара
- 7. Куб вписан в шар радиус которого равен
- 8. Обозначим диагональ буквой d, а ребро куба буквой a.
- 9. Цилиндр и конус имеют общее основание и
- 10. Цилиндр и конус имеют общие основание и
- 11. 1.Цилиндр и конус имеют общее основание
- 12. ИтогИспользуя указанные формулы при данных величинах объёма
- 13. Найдите объем многогранника, вершинами которого являются точки
- 14. Найдите объем многогранника, вершинами которого являются точки
- 15. Найдите объем многогранника, вершинами которого являются точки
- 16. Найдите объем многогранника, вершинами которого являются точки
- 17. Данная презентация предназначена для подготовки к ЕГЭ,
Слайд 2Формулы которые необходимо знать!
Формула объёма шара:
Формула площади поверхности шара:
Формула объёма цилиндра:
Формула
Слайд 3Особенности представленных задач
1. Если шар вписан в цилиндр, то у них
2. Высота цилиндра описанного около шара равна двум его радиусам (или диаметру).
3. Если куб вписан в шар, то диагональ этого куба равна диаметру шара.
Слайд 4
Необходимо найти радиус шара.
У шара и у цилиндра общий радиус. Основание
Ответ: 22
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
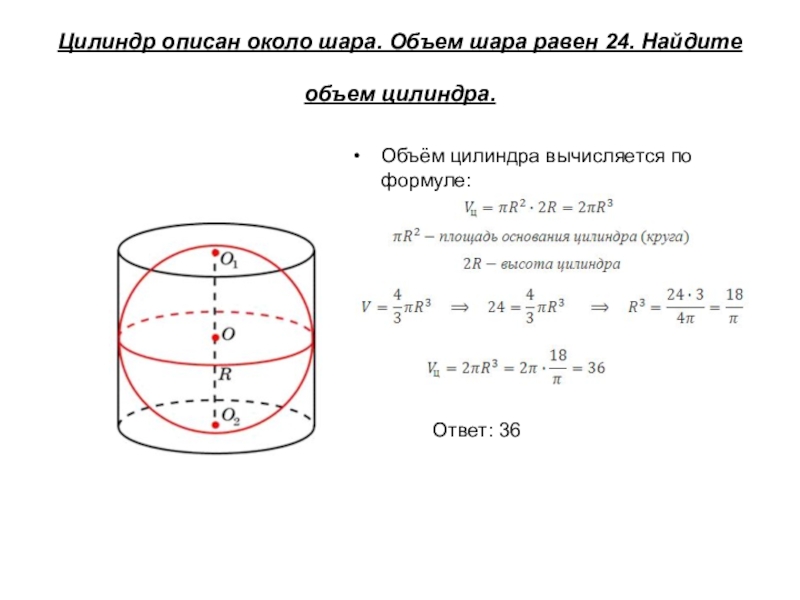
Слайд 5Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Объём цилиндра вычисляется по формуле:
Ответ: 36
Слайд 6Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь
Упростим:
Формула поверхности шара:
Формула поверхности цилиндра:
Так как площадь поверхности шара нам дана, то мы можем выразить радиус:
Далее подставим его в формулу площади поверхности цилиндра и вычислить её, таким образом:
Ответ: 166,5
Слайд 7Куб вписан в шар радиус которого равен корню из трёх. Найдите
Чтобы вычислить объём куба необходимо знать чему равно его ребро. Радиус шара равен половине диагонали куба:
*Диагональ куба равна диаметру шара.
Значит диагональ куба будет равна двум корням из трёх.
Слайд 8
Обозначим диагональ буквой d, а ребро куба буквой a. Нам известна формула выражающая
Значит мы можем вычислить ребро куба:
Таким образом, объём куба будет равен 23 = 8.
Ответ: 8
Слайд 9Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем
Объем цилиндра равен произведению площади основания на высоту, а объем конуса равен одной трети произведения площади основания на высоту.
Поскольку они имеют общее основание и высоту, получается, что объем цилиндра будет в три раза больше объема конуса.
Таким образом он равен 120.
Видно, что объём конуса составляет третью часть от объёма цилиндра.
Ответ: 120
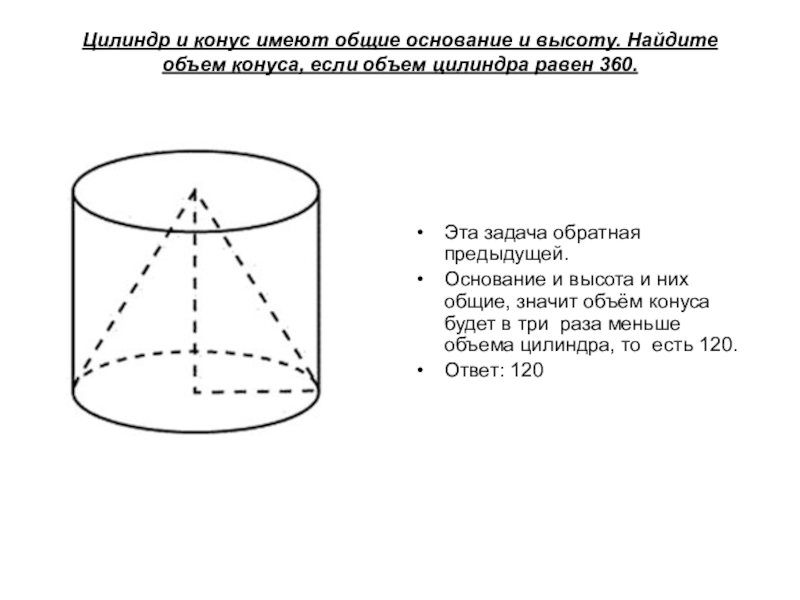
Слайд 10Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если
Эта задача обратная предыдущей.
Основание и высота и них общие, значит объём конуса будет в три раза меньше объема цилиндра, то есть 120.
Ответ: 120
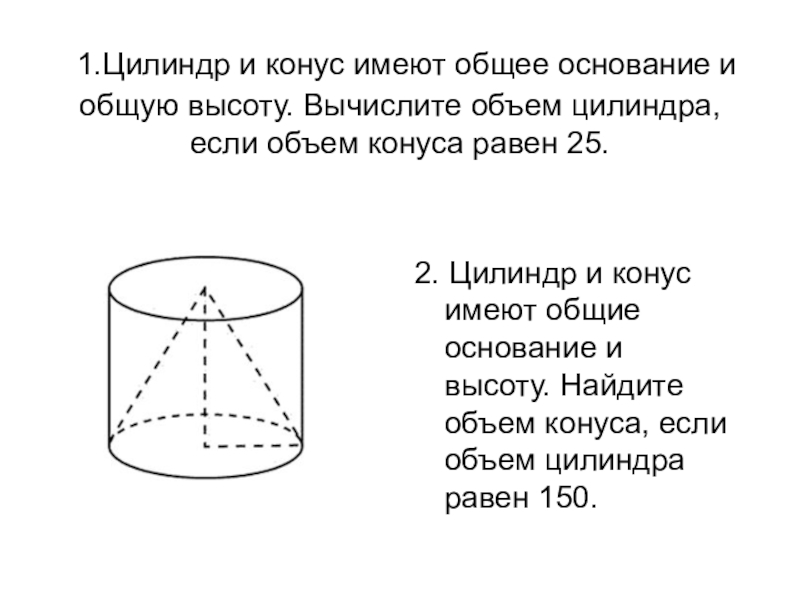
Слайд 11 1.Цилиндр и конус имеют общее основание и общую высоту. Вычислите
2. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Слайд 12Итог
Используя указанные формулы при данных величинах объёма или площади поверхности всегда
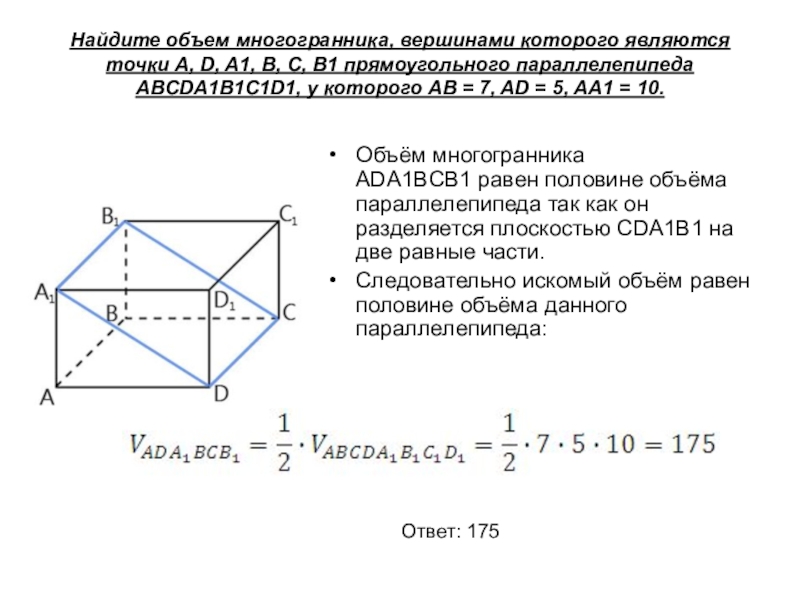
Слайд 13Найдите объем многогранника, вершинами которого являются точки A, D, A1, B,
Объём многогранника ADA1BCB1 равен половине объёма параллелепипеда так как он разделяется плоскостью CDA1B1 на две равные части.
Следовательно искомый объём равен половине объёма данного параллелепипеда:
Ответ: 175
Слайд 14Найдите объем многогранника, вершинами которого являются точки D, B, B1, C1,
Многогранник DBB1C1 это пирамида с основанием BB1C1 вершиной D при чём высота этой пирамиды равна AB (АВ=СD).
Конечно, данную пирамиду можно представить и с другим основанием и высотой, но тогда будет сложно и долго производить вычисления. В данном же случае площадь BB1C1 найти просто – это прямоугольный треугольник с известными катетами, АВ так же известна.
Таким образом, искомый объём равен:
Ответ: 54
Соединим указанные вершины:
Слайд 15Найдите объем многогранника, вершинами которого являются точки A1, B, C, C1,
Соединим указанные вершины:
Многогранник A1BCC1B1 это пирамида с основанием BCC1B1, вершиной A1 и высотой равной AB.
Таким образом, искомый объём равен:
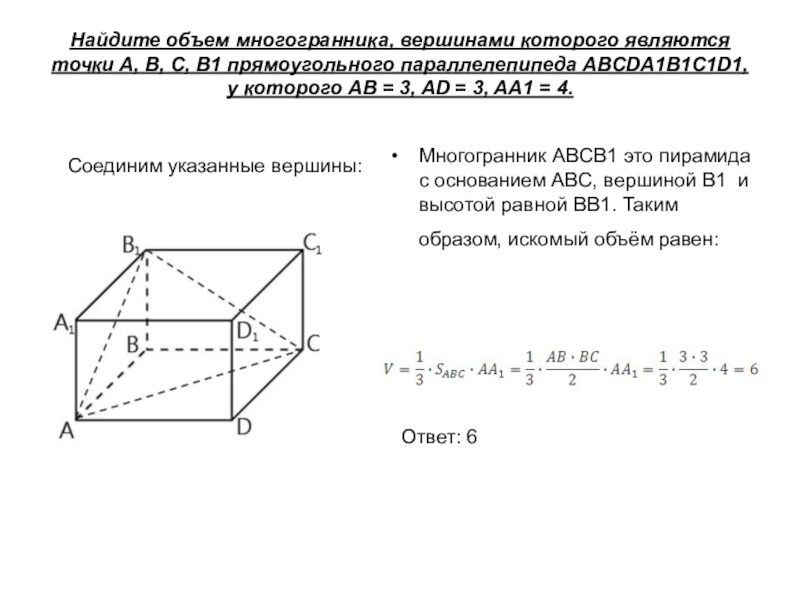
Слайд 16Найдите объем многогранника, вершинами которого являются точки A, B, C, B1 прямоугольного
Многогранник ABCB1 это пирамида с основанием ABC, вершиной B1 и высотой равной BB1. Таким образом, искомый объём равен:
Соединим указанные вершины:
Ответ: 6
Слайд 17
Данная презентация предназначена для подготовки к ЕГЭ, позволяет отработать навыки решения
Использованы материалы Тематической рабочей тетради под ред. И.В.Ященко ЕГЭ 2016. Математика. 20 вариантов тестов. М.: МЦНМО, издательство «Экзамен», 2016