край Михайловский р-н
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Показательные уравнения и неравенства. Презентация к уроку
Содержание
- 1. Показательные уравнения и неравенства. Презентация к уроку
- 2. Показательными называются уравнения, в которых неизвестная величина находится в показателе степени.
- 3. Слайд 3
- 4. Решение.Это уравнение равносильно квадратному :
- 5. Слайд 5
- 6. Решение.Чтобы решить это уравнение , нужно привести
- 7. Основная сложность решения таких уравнений заключается в
- 8. Решение.Приведем левую и правую части уравнения к
- 9. Слайд 9
- 10. Решение.илиЧтобы было ясно , какое выражение выносить за скобки , преобразуем показатели степеней:Решение.
- 11. Условно эти уравнения можно классифицировать как однородные показательные уравнения первой степени.
- 12. Решение.Перенося все слагаемые в левую часть , приведем уравнение к стандартной форме:или
- 13. Решение .или
- 14. Уравнения вида αa2f(x)+βaf(x)+ϒ=0 заменой y=af(x) сводятся к квадратному.
- 15. Решение .Решить уравнение : 25x – 6
- 16. Решение.Для решения этого примера нужно применить тригонометрические
- 17. Слайд 17
- 18. Решить уравнение : 4x+2•6x-3•9x=0Решение .Заметим, что 4=22,
- 19. Слайд 19
- 20. Решение. Заметим, чтоилиy2 -18y +1=0x1=2x2=-2Ответ: x1 ,2 = ±2
- 21. Уравнения вида [f(x)] g(x)=1 относятся к частному
- 22. Решение.Первое равносильное уравнение 3x2-10x+3=0 при x-3>0.Оба корня
- 23. Степенно-показательные уравнения [f(x)]ϕ(x)=[f(x)]ψ(x),как и в предыдущем случае,
- 24. Решение. Первое равносильное уравнение x2+2x=11x-20 с условием
- 25. Уравнения вида F(a f(x)) = 0 заменой
- 26. 15t(t-6)+8t(t+1)=6(t+1)(t-6)15t2-90t+8t2+8t=6t2-30t-3617t2-52t+36=0t1=22x=2x1= 1 t=2x
- 27. Решение.Решаем первое неравенство :Решаем второе неравенство :2x
- 28. Материал взят из книги «Полный курс подготовки
Показательными называются уравнения, в которых неизвестная величина находится в показателе степени.
Слайд 1«Показательные уравнения»
Презентация к уроку . 16 1218г.
Составлена учителем математики
МКОУ «Ракитовская СОШ»Алтайский
Слайд 2Показательными называются уравнения, в которых неизвестная величина находится в показателе степени.
Слайд 6Решение.
Чтобы решить это уравнение , нужно привести его к одному основанию
.
Заметим , что
тогда
Равносильное уравнение
Слайд 7Основная сложность решения таких уравнений заключается в приведении левой и правой
частей уравнения к одному основанию.
Слайд 8Решение.
Приведем левую и правую части уравнения к основанию 2 :
Тогда
или
откуда
После приведения
к общему знаменателю и простых преобразований получаем :
или
Ответ : х = 10
Слайд 10Решение.
или
Чтобы было ясно , какое выражение выносить за скобки , преобразуем
показатели степеней:
Решение.
Слайд 11Условно эти уравнения можно классифицировать как однородные показательные уравнения первой степени.
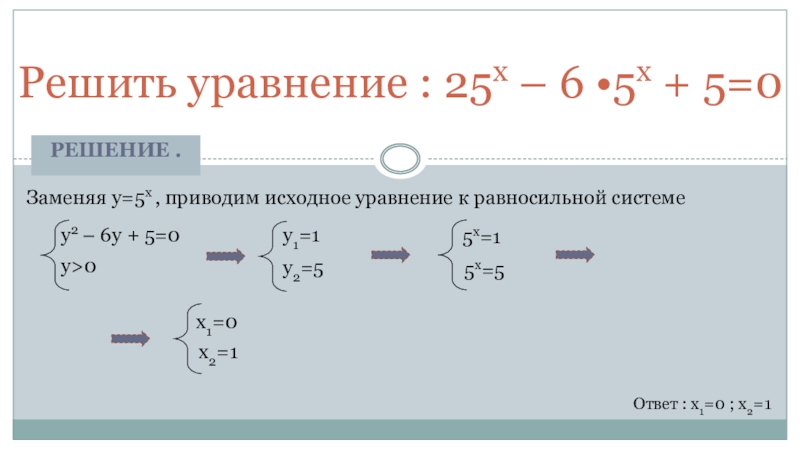
Слайд 15Решение .
Решить уравнение : 25x – 6 •5x + 5=0
Заменяя y=5x
, приводим исходное уравнение к равносильной системе
y2 – 6y + 5=0
y>0
y1=1
y2=5
5x=1
x1=0
5x=5
Ответ : x1=0 ; x2=1
x2=1
Слайд 16Решение.
Для решения этого примера нужно применить тригонометрические преобразования, а именно
тогда уравнение
примет вид
4y2- y – 3=0
положительный корень равен 1,
или tg x=0,
откуда x=πn , n ϵ Z.
Ответ : x=πn , n ϵ Z.
Слайд 18Решить уравнение : 4x+2•6x-3•9x=0
Решение .
Заметим, что
4=22, 6 =2 • 3,
9=32,
и перепишем исходное уравнение в виде
22x+2•2x•3x-3•32x=0.
Ответ : x=0
y >0
положительный корень y =1 ,
y2+2y-3=0
Слайд 21Уравнения вида [f(x)] g(x)=1 относятся к частному случаю степенно-показательных уравнений, когда
неизвестная величина находится не только в показателе степени, но и в основании. Два равносильных уравнения: g(x)=0 при f(x)>0, т.к. Любое число в нулевой степени есть единица, и f(x)=1.
![Уравнения вида [f(x)] g(x)=1 относятся к частному случаю степенно-показательных уравнений, когда неизвестная величина находится не только в](/img/thumbs/d6a5ee6fb2ee0a39c9e20ff0b7b7321b-800x.jpg "Показательные уравнения и неравенства. Презентация к уроку Уравнения вида [f(x)] g(x)=1 относятся к частному случаю степенно-показательных уравнений, когда")
Слайд 22Решение.
Первое равносильное уравнение 3x2-10x+3=0 при x-3>0.
Оба корня не подходят, поскольку не
удовлетворяют условию x – 3 > 0.
Второе равносильное уравнение x – 3 =1, откуда x = 4.
Ответ : x = 4
Слайд 23Степенно-показательные уравнения [f(x)]ϕ(x)=[f(x)]ψ(x),как и в предыдущем случае, сводятся к двум равносильным
: ϕ(x)=ψ(x) при условии f(x)>0 и f(x)=1
![Степенно-показательные уравнения [f(x)]ϕ(x)=[f(x)]ψ(x),как и в предыдущем случае, сводятся к двум равносильным : ϕ(x)=ψ(x) при условии f(x)>0 и](/img/thumbs/72b9d382223e3aa65fd50223bf4b41ca-800x.jpg "Показательные уравнения и неравенства. Презентация к уроку Степенно-показательные уравнения [f(x)]ϕ(x)=[f(x)]ψ(x),как и в предыдущем случае, сводятся к двум равносильным")
Слайд 24Решение.
Первое равносильное уравнение x2+2x=11x-20 с условием x-2>0
имеет корни x1=4
, x2=5.
Второе равносильное уравнение x-2=1
дает третий корень x3=3
Ответ: x1=4 , x2=5 , x3=3.
Слайд 25Уравнения вида F(a f(x)) = 0 заменой переменной t =
a f(x) приводятся к алгебраическому F(t) = 0 при условии t > 0.
Слайд 27Решение.
Решаем первое неравенство :
Решаем второе неравенство :
2x • 2-1 – 7
• 2x • 2-1 + 5 ≤ 0
t2 – 7t + 10 ≤ 0
t2 – 7t + 10 = 0
t1=5
t2=2
2x=5
2x=2
x=1
x≠2
x≠3
2x=t , t>0
2
1
1
3
Слайд 28Материал взят из книги «Полный курс подготовки к выпускным экзаменам» под
редакцией Б.Черкасова
учитель математики – Абрамова Светлана Ивановна
Оформление слайдов взято из Интернета
16.12.2018
Неравенства С3-группы из ЕГЭ 2014г.
